Question Number 160050 by tounghoungko last updated on 24/Nov/21
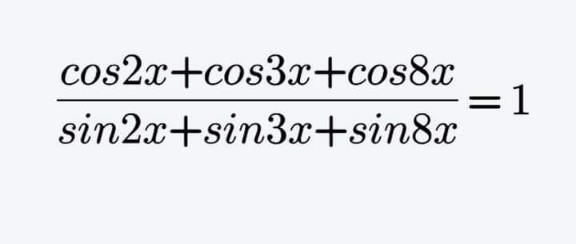
Answered by mindispower last updated on 24/Nov/21

$${cos}\left({a}\right)+{cos}\left({b}\right)=\mathrm{2}{cos}\left(\frac{{a}−{b}}{\mathrm{2}}\right){cos}\left(\frac{{a}+{b}}{\mathrm{2}}\right) \\ $$$${sin}\left({a}\right)+\mathrm{sin}\left(\mathrm{b}\right)=\mathrm{2cos}\left(\frac{\mathrm{a}−\mathrm{b}}{\mathrm{2}}\right)\mathrm{sin}\left(\frac{\mathrm{a}+\mathrm{b}}{\mathrm{2}}\right) \\ $$$$\Leftrightarrow\frac{{cos}\left(\mathrm{3}{x}\right)\left(\mathrm{2}{cos}\left(\mathrm{5}{x}\right)+\mathrm{1}\right)}{{cos}\left(\mathrm{3}{x}\right)\left(\mathrm{2}{sin}\left(\mathrm{5}{x}\right)+\mathrm{1}\right)}=\mathrm{1} \\ $$$$\forall{x}\in\mathbb{R}−\left\{{cos}\left(\mathrm{3}{x}\right)=\mathrm{0}\right\} \\ $$$$\Leftrightarrow{sin}\left(\mathrm{5}{x}\right)={cos}\left(\mathrm{5}{x}\right)\:{easy}\:{now} \\ $$
