Question Number 160142 by cortano last updated on 25/Nov/21
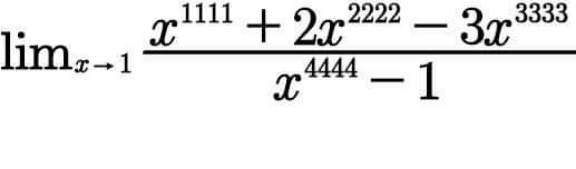
Answered by puissant last updated on 25/Nov/21

$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{{x}^{\mathrm{1111}} +\mathrm{2}{x}^{\mathrm{2222}} −\mathrm{3}{x}^{\mathrm{3333}} }{{x}^{\mathrm{4444}} −\mathrm{1}}\: \\ $$$$=\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\frac{{d}}{{dx}}\left\{{x}^{\mathrm{1111}} +\mathrm{2}{x}^{\mathrm{2222}} −\mathrm{3}{x}^{\mathrm{3333}} \right\}}{\frac{{d}}{{dx}}\left\{{x}^{\mathrm{4444}} −\mathrm{1}\right\}} \\ $$$$=\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\mathrm{1111}{x}^{\mathrm{1110}} +\mathrm{4444}{x}^{\mathrm{2221}} −\mathrm{9999}{x}^{\mathrm{3332}} }{\mathrm{4444}{x}^{\mathrm{4443}} } \\ $$$$=\:\frac{\mathrm{1111}+\mathrm{4444}−\mathrm{9999}}{\mathrm{4444}}\:=\:−\frac{\mathrm{4444}}{\mathrm{4444}}\:=\:−\mathrm{1}.. \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:…………\mathscr{L}{e}\:{puissant}………… \\ $$
Commented by cortano last updated on 25/Nov/21

$${yes} \\ $$
Answered by Rasheed.Sindhi last updated on 25/Nov/21

$$\succ_{\:\curlywedge} ^{\:\curlyvee} \mathrm{Without}\:\mathrm{Using}\:\mathrm{Calculus}_{\curlywedge} ^{\curlyvee} \prec \\ $$$$\mathrm{lim}\frac{{x}^{\mathrm{1111}} +\mathrm{2}{x}^{\mathrm{2222}} −\mathrm{3}{x}^{\mathrm{3333}} }{{x}^{\mathrm{4444}} −\mathrm{1}} \\ $$$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{{x}^{\mathrm{1111}} −{x}^{\mathrm{2222}} +\mathrm{3}{x}^{\mathrm{2222}} −\mathrm{3}{x}^{\mathrm{3333}} }{{x}^{\mathrm{4444}} −\mathrm{1}} \\ $$$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{{x}^{\mathrm{1111}} \left(\mathrm{1}−{x}^{\mathrm{1111}} \right)+\mathrm{3}{x}^{\mathrm{2222}} \left(\mathrm{1}−{x}^{\mathrm{1111}} \right)}{\left({x}^{\mathrm{2222}} −\mathrm{1}\right)\left({x}^{\mathrm{2222}} +\mathrm{1}\right)} \\ $$$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{−\cancel{\left({x}^{\mathrm{1111}} −\mathrm{1}\right)}\left({x}^{\mathrm{1111}} +\mathrm{3}{x}^{\mathrm{2222}} \right)}{\cancel{\left({x}^{\mathrm{1111}} −\mathrm{1}\right)}\left({x}^{\mathrm{1111}} +\mathrm{1}\right)\left({x}^{\mathrm{2222}} +\mathrm{1}\right)} \\ $$$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{−\left({x}^{\mathrm{1111}} +\mathrm{3}{x}^{\mathrm{2222}} \right)}{\left({x}^{\mathrm{1111}} +\mathrm{1}\right)\left({x}^{\mathrm{2222}} +\mathrm{1}\right)}=\frac{−\left(\mathrm{1}+\mathrm{3}\right)}{\left(\mathrm{1}+\mathrm{1}\right)\left(\mathrm{1}+\mathrm{1}\right)} \\ $$$$=\frac{−\mathrm{4}}{\mathrm{4}}=−\mathrm{1} \\ $$
Commented by puissant last updated on 25/Nov/21
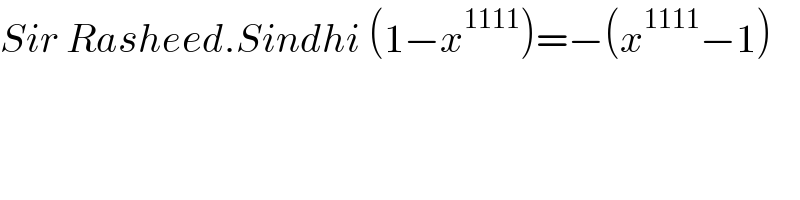
$${Sir}\:{Rasheed}.{Sindhi}\:\left(\mathrm{1}−{x}^{\mathrm{1111}} \right)=−\left({x}^{\mathrm{1111}} −\mathrm{1}\right) \\ $$
Commented by Rasheed.Sindhi last updated on 25/Nov/21
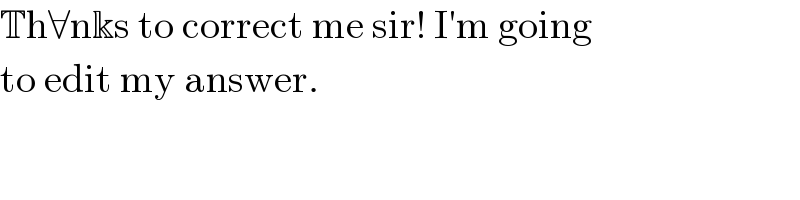
$$\mathbb{T}\mathrm{h}\forall\mathrm{n}\Bbbk\mathrm{s}\:\mathrm{to}\:\mathrm{correct}\:\mathrm{me}\:\mathrm{sir}!\:\mathrm{I}'\mathrm{m}\:\mathrm{going} \\ $$$$\mathrm{to}\:\mathrm{edit}\:\mathrm{my}\:\mathrm{answer}. \\ $$
Commented by cortano last updated on 25/Nov/21

$${okay} \\ $$
