Question Number 160205 by Tawa11 last updated on 25/Nov/21

Answered by mr W last updated on 26/Nov/21
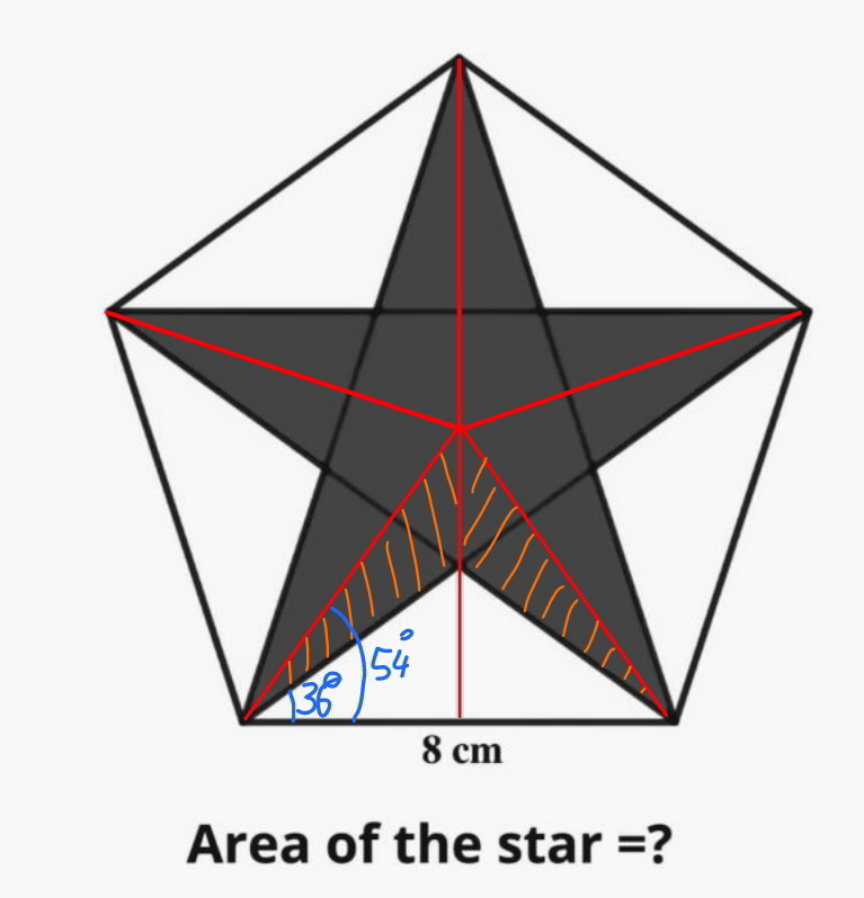
Commented by mr W last updated on 26/Nov/21

$${orange}\:{shaded}\:{area}\: \\ $$$$=\frac{\mathrm{8}}{\mathrm{2}}×\mathrm{4}\:\mathrm{tan}\:\mathrm{54}°−\frac{\mathrm{8}}{\mathrm{2}}×\mathrm{4}\:\mathrm{tan}\:\mathrm{36}° \\ $$$$=\mathrm{16}\:\left(\mathrm{tan}\:\mathrm{54}°−\mathrm{tan}\:\mathrm{36}°\right) \\ $$$${area}\:{of}\:{star}\:=\mathrm{5}×\mathrm{16}\:\left(\mathrm{tan}\:\mathrm{54}°−\mathrm{tan}\:\mathrm{36}°\right) \\ $$$$=\mathrm{80}\left(\mathrm{tan}\:\mathrm{54}°−\mathrm{tan}\:\mathrm{36}°\right)\approx\mathrm{51}.\mathrm{987}\:{cm}^{\mathrm{2}} \\ $$$$ \\ $$$$\underline{{exact}\:{form}:} \\ $$$$\mathrm{sin}\:\mathrm{18}°=\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{4}} \\ $$$$\mathrm{cos}\:\mathrm{36}°=\mathrm{1}−\mathrm{2}\left(\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{4}}\right)^{\mathrm{2}} =\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{4}} \\ $$$$\mathrm{tan}\:\mathrm{36}°=\sqrt{\left(\frac{\mathrm{4}}{\:\sqrt{\mathrm{5}}+\mathrm{1}}\right)^{\mathrm{2}} −\mathrm{1}}=\sqrt{\mathrm{5}−\mathrm{2}\sqrt{\mathrm{5}}} \\ $$$$\mathrm{tan}\:\mathrm{54}°=\frac{\mathrm{1}}{\mathrm{tan}\:\mathrm{36}°} \\ $$$$\mathrm{tan}\:\mathrm{54}°−\mathrm{tan}\:\mathrm{36}°=\frac{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \:\mathrm{36}°}{\mathrm{tan}\:\mathrm{36}°} \\ $$$$=\frac{\mathrm{1}−\mathrm{5}+\mathrm{2}\sqrt{\mathrm{5}}}{\:\sqrt{\mathrm{5}−\mathrm{2}\sqrt{\mathrm{5}}}}=\frac{\mathrm{2}\left(\sqrt{\mathrm{5}}−\mathrm{2}\right)}{\:\sqrt{\sqrt{\mathrm{5}}\left(\sqrt{\mathrm{5}}−\mathrm{2}\right)}}=\frac{\mathrm{2}\sqrt{\mathrm{5}\left(\mathrm{5}−\mathrm{2}\sqrt{\mathrm{5}}\right)}}{\:\mathrm{5}} \\ $$$${area}\:{of}\:{star}=\mathrm{80}×\frac{\mathrm{2}\sqrt{\mathrm{5}\left(\mathrm{5}−\mathrm{2}\sqrt{\mathrm{5}}\right)}}{\:\mathrm{5}} \\ $$$$=\mathrm{32}\sqrt{\mathrm{5}\left(\mathrm{5}−\mathrm{2}\sqrt{\mathrm{5}}\right)} \\ $$
Commented by Tawa11 last updated on 26/Nov/21
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate} \\ $$
Answered by amin96 last updated on 25/Nov/21
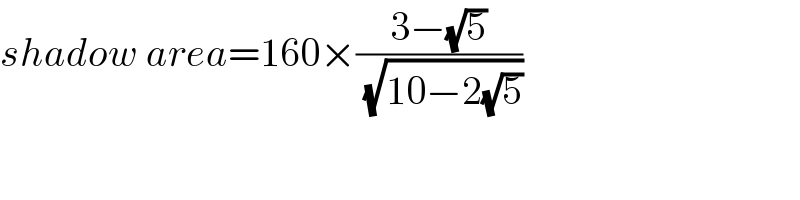
$${shadow}\:{area}=\mathrm{160}×\frac{\mathrm{3}−\sqrt{\mathrm{5}}}{\:\sqrt{\mathrm{10}−\mathrm{2}\sqrt{\mathrm{5}}}} \\ $$
Commented by Tawa11 last updated on 26/Nov/21
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate} \\ $$
Answered by 1549442205PVT last updated on 26/Nov/21

$${we}\:{have}\:{sin}\mathrm{36}^{\mathrm{0}} ={cos}\mathrm{54}^{\mathrm{0}} \Rightarrow\mathrm{2}{sin}\mathrm{18}^{\mathrm{0}} {cos}\mathrm{18}^{\mathrm{0}} =\mathrm{3}{cos}.\mathrm{318}^{\mathrm{0}} \\ $$$$\Rightarrow\mathrm{2}{sin}\mathrm{18}^{\mathrm{0}} {cos}\mathrm{18}^{\mathrm{0}} =\mathrm{4}{cos}^{\mathrm{3}} \mathrm{18}^{\mathrm{0}} −\mathrm{3}{cos}\mathrm{18}^{\mathrm{0}} \\ $$$$\Rightarrow\mathrm{4}{cos}^{\mathrm{2}} \mathrm{18}^{\mathrm{0}} −\mathrm{3}=\mathrm{2}{sin}\mathrm{18}^{\mathrm{0}} \Rightarrow\mathrm{4}\left(\mathrm{1}−{sin}^{\mathrm{2}} \mathrm{18}^{\mathrm{0}} \right)−\mathrm{3}=\mathrm{2}{sin}\mathrm{18}^{\mathrm{0}} \\ $$$$\Rightarrow\mathrm{4}{sin}^{\mathrm{2}} \mathrm{18}^{\mathrm{0}} +\mathrm{2}{sin}\mathrm{18}^{\mathrm{0}} −\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow{sin}\mathrm{18}^{\mathrm{0}} =\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{4}}.{From}\:{that}\:{we}\:{have} \\ $$$${cos}\mathrm{18}^{\mathrm{0}} =\frac{\sqrt{\mathrm{10}+\mathrm{2}\sqrt{\mathrm{5}}}}{\mathrm{4}} \\ $$$${cos}\mathrm{36}^{\mathrm{0}} =\mathrm{1}−\mathrm{2}{sin}^{\mathrm{2}} \mathrm{18}^{\mathrm{0}} =\mathrm{1}−\frac{\mathrm{3}−\sqrt{\mathrm{5}}}{\mathrm{4}}=\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{4}} \\ $$$${sin}\mathrm{36}^{\mathrm{0}} =\sqrt{\mathrm{1}−{cos}^{\mathrm{2}} \mathrm{36}^{\mathrm{0}} }=\frac{\sqrt{\mathrm{10}−\mathrm{2}\sqrt{\mathrm{5}}}}{\mathrm{4}}, \\ $$$${tan}\mathrm{36}^{\mathrm{0}} =\frac{\sqrt{\mathrm{10}−\mathrm{2}\sqrt{\mathrm{5}}}}{\:\sqrt{\mathrm{5}+\mathrm{1}}} \\ $$$${The}\:{altitude}\:{of}\:{every}\:{white}\:{triangle}\:{is}\:{equal} \\ $$$${h}_{\mathrm{0}} =\mathrm{4}×{tan}\mathrm{36}^{\mathrm{0}} =\left(\sqrt{\mathrm{5}}−\mathrm{1}\right)\sqrt{\mathrm{10}−\mathrm{2}\sqrt{\mathrm{5}}.}{Hence} \\ $$$${the}\:{area}\:{of}\:{every}\:{white}\:{triangle}\:{is} \\ $$$$\left.{s}_{\mathrm{0}} \left.=\frac{\mathrm{1}}{\mathrm{2}}{mh}_{\mathrm{0}} =\frac{\mathrm{1}}{\mathrm{2}}\mathrm{8}.\left(\sqrt{\mathrm{5}}−\mathrm{1}\right)\sqrt{\mathrm{10}−\mathrm{2}\sqrt{\mathrm{5}}}\right)=\mathrm{4}\left(\sqrt{\mathrm{5}}−\mathrm{1}\right)\sqrt{\mathrm{10}−\mathrm{2}\sqrt{\mathrm{5}}}\right) \\ $$$${Basa}\:{of}\:{it}\:{equal}\:{to}\:{b}=\mathrm{8}+\mathrm{2}.\mathrm{8}{sin}\mathrm{18}=\mathrm{4}\left(\sqrt{\mathrm{5}}+\mathrm{1}\right) \\ $$$${the}\:{altitude}\:{of}\:{the}\:{start}'{s}\:{wing}\:{is} \\ $$$${h}_{\mathrm{2}} =\mathrm{8}.{sin}\mathrm{36}^{\mathrm{0}} =\mathrm{2}\sqrt{\mathrm{10}−\mathrm{2}\sqrt{\mathrm{5}}}.{The}\:{area}\:{of}\:{every}\:\: \\ $$$${the}\:{altitude}\:{of}\:{the}\:{triangle}\:{with}\:{the}\:{lateral}\:{side}\:{b}\:{and}\:{the}\:{base}\:{m}=\mathrm{8}{cm} \\ $$$${equal}\:{to}\:{h}_{\mathrm{3}} ={bcos}\mathrm{18}^{\mathrm{0}} =\left(\sqrt{\mathrm{5}}+\mathrm{1}\right)\sqrt{\mathrm{10}+\mathrm{2}\sqrt{\mathrm{5}}} \\ $$$${the}\:{are}\:{of}\:{the}\:{triangle}\:{with}\:{the}\:{side}\:{b}\:{and}\:{altitude}\:{h}_{\mathrm{2}} {be}: \\ $$$${equal}\:{to}\:{s}_{\mathrm{2}} =\:\frac{\mathrm{1}}{\mathrm{2}}{bh}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{4}\left(\sqrt{\mathrm{5}}+\mathrm{1}\right)\sqrt{\mathrm{10}−\mathrm{2}\sqrt{\mathrm{5}}}=\mathrm{2}\left(\sqrt{\mathrm{5}}+\mathrm{1}\right)\sqrt{\mathrm{10}−\mathrm{2}\sqrt{\mathrm{5}{u}}} \\ $$$${the}\:{are}\:{of}\:{the}\:{triangle}\:{with}\:{the}\:{lateral}\:{side}\:{b}\:{and}\:{altitude}\:{h}_{\mathrm{3}} {be}: \\ $$$${s}_{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{2}}{mh}_{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{2}}.\mathrm{8}.\left(\sqrt{\mathrm{5}}+\mathrm{1}\right)\sqrt{\mathrm{10}+\mathrm{2}\sqrt{\mathrm{5}}}=\mathrm{4}\left(\sqrt{\mathrm{5}}+\mathrm{1}\sqrt{\mathrm{10}+\mathrm{2}\sqrt{\mathrm{5}}}\right. \\ $$$${the}\:{of}\:{the}\:\:{pentagon}\:{equal}\:{to} \\ $$$${S}={s}_{\mathrm{3}} +\mathrm{2}{s}_{\mathrm{2}} =\mathrm{4}\left(\sqrt{\mathrm{5}}+\mathrm{1}\right)\sqrt{\mathrm{10}+\mathrm{2}\sqrt{\mathrm{5}}}+\mathrm{2}.\mathrm{2}\left(\sqrt{\mathrm{5}}+\mathrm{1}\right)\sqrt{\mathrm{10}−\mathrm{2}\sqrt{\mathrm{5}}} \\ $$$$=\mathrm{4}\left(\sqrt{\mathrm{5}}+\mathrm{1}\right).\mathrm{4}\sqrt{\mathrm{5}}=\mathrm{16}\left(\mathrm{5}+\sqrt{\mathrm{5}}\right) \\ $$$${the}\:{of}\:{the}\:{star}\:{is}:{s}={S}−\mathrm{5}{s}_{\mathrm{0}} \\ $$$$=\mathrm{16}\left(\mathrm{5}+\sqrt{\left.\mathrm{5}\right)}−\mathrm{5}.\mathrm{4}\left(\sqrt{\mathrm{5}}−\mathrm{1}\right)\sqrt{\mathrm{10}−\mathrm{2}\sqrt{\mathrm{5}}}\right) \\ $$$$\approx\mathrm{57}.\mathrm{654} \\ $$
Commented by Tawa11 last updated on 26/Nov/21
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate} \\ $$
