Question-160221

Question Number 160221 by HongKing last updated on 26/Nov/21

Commented by mr W last updated on 26/Nov/21

if question is right, then answer is wrong. if answer is right, then question is wrong. ⇒typo!

$${if}\:{question}\:{is}\:{right},\:{then}\:{answer}\:{is} \\ $$$${wrong}.\:{if}\:{answer}\:{is}\:{right},\:{then}\: \\ $$$${question}\:{is}\:{wrong}. \\ $$$$\Rightarrow{typo}! \\ $$

Commented by quvonnn last updated on 26/Nov/21

$$ \\ $$

Commented by Rasheed.Sindhi last updated on 26/Nov/21

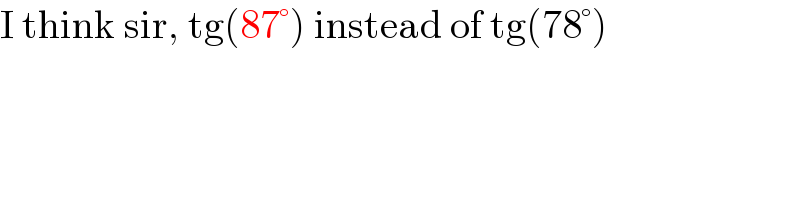
$$\mathrm{I}\:\mathrm{think}\:\mathrm{sir},\:\mathrm{tg}\left(\mathrm{87}°\right)\:\mathrm{instead}\:\mathrm{of}\:\mathrm{tg}\left(\mathrm{78}°\right) \\ $$

Commented by quvonnn last updated on 26/Nov/21

Answered by Rasheed.Sindhi last updated on 26/Nov/21

tg(1).tg(2).tg(3).....tg(87).tg(88).tg(89)=1 tanθtan(90−θ)=1 tan(90−θ)=tan(45+(45−θ)) =((tan45+tan(45−θ) )/(1−tan45tan(45−θ) )) tan(45−θ)=((tan45−tanθ )/(1+tan45tanθ ))=((1−tanθ )/(1+tanθ )) =((1+((1−tanθ )/(1+tanθ )) )/(1−(1)(((1−tanθ )/(1+tanθ ))) ))=((1+tanθ+1−tanθ )/(1+tanθ−1+tanθ )) =(2/(2tanθ ))=(1/(tanθ )) ∴ tanθtan(90−θ)=1 LHS: (tan1tan89)(tan2tan88)...(tan45tan45) =1.1.1....1_(45 times) =1^(45) =1=RHS

$$\mathrm{tg}\left(\mathrm{1}\right).\mathrm{tg}\left(\mathrm{2}\right).\mathrm{tg}\left(\mathrm{3}\right)…..\mathrm{tg}\left(\mathrm{87}\right).\mathrm{tg}\left(\mathrm{88}\right).\mathrm{tg}\left(\mathrm{89}\right)=\mathrm{1} \\ $$$$\mathrm{tan}\theta\mathrm{tan}\left(\mathrm{90}−\theta\right)=\mathrm{1} \\ $$$$\:\mathrm{tan}\left(\mathrm{90}−\theta\right)=\mathrm{tan}\left(\mathrm{45}+\left(\mathrm{45}−\theta\right)\right) \\ $$$$=\frac{\mathrm{tan45}+\mathrm{tan}\left(\mathrm{45}−\theta\right)\:\:}{\mathrm{1}−\mathrm{tan45tan}\left(\mathrm{45}−\theta\right)\:\:}\: \\ $$$$\mathrm{tan}\left(\mathrm{45}−\theta\right)=\frac{\mathrm{tan45}−\mathrm{tan}\theta\:\:}{\mathrm{1}+\mathrm{tan45tan}\theta\:\:}=\frac{\mathrm{1}−\mathrm{tan}\theta\:}{\mathrm{1}+\mathrm{tan}\theta\:} \\ $$$$=\frac{\mathrm{1}+\frac{\mathrm{1}−\mathrm{tan}\theta\:}{\mathrm{1}+\mathrm{tan}\theta\:}\:\:}{\mathrm{1}−\left(\mathrm{1}\right)\left(\frac{\mathrm{1}−\mathrm{tan}\theta\:}{\mathrm{1}+\mathrm{tan}\theta\:}\right)\:\:}=\frac{\mathrm{1}+\mathrm{tan}\theta+\mathrm{1}−\mathrm{tan}\theta\:\:}{\mathrm{1}+\mathrm{tan}\theta−\mathrm{1}+\mathrm{tan}\theta\:} \\ $$$$=\frac{\mathrm{2}}{\mathrm{2tan}\theta\:}=\frac{\mathrm{1}}{\mathrm{tan}\theta\:} \\ $$$$\therefore\:\:\:\:\mathrm{tan}\theta\mathrm{tan}\left(\mathrm{90}−\theta\right)=\mathrm{1} \\ $$$$ \\ $$$$\mathrm{LHS}: \\ $$$$\left(\mathrm{tan1tan89}\right)\left(\mathrm{tan2tan88}\right)…\left(\mathrm{tan45tan45}\right) \\ $$$$=\underset{\mathrm{45}\:\mathrm{times}} {\mathrm{1}.\mathrm{1}.\mathrm{1}….\mathrm{1}}=\mathrm{1}^{\mathrm{45}} =\mathrm{1}=\mathrm{RHS}\:\:\:\:\:\:\:\: \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply