Question Number 160241 by mathlove last updated on 26/Nov/21
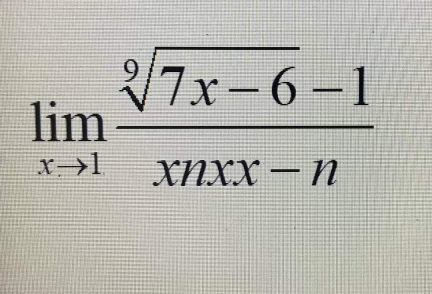
Commented by blackmamba last updated on 26/Nov/21

$$\:\:\:\:\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\sqrt[{\mathrm{9}}]{\mathrm{7}{x}−\mathrm{6}}−\mathrm{1}}{{nx}^{\mathrm{3}} −{n}}\: \\ $$$$\:\:\:\:\:=\:\frac{\mathrm{1}}{{n}}\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\sqrt[{\mathrm{9}}]{\mathrm{7}{x}−\mathrm{6}}−\mathrm{1}}{\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)\left({x}−\mathrm{1}\right)} \\ $$$$\:\:\:\:\:=\:\frac{\mathrm{1}}{\mathrm{3}{n}}\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\sqrt[{\mathrm{9}}]{\mathrm{7}{x}−\mathrm{6}}−\mathrm{1}}{{x}−\mathrm{1}}\: \\ $$$$\:{let}\:\mathrm{7}{x}−\mathrm{6}\:=\:{u}^{\mathrm{9}} \\ $$$$\:\:\:\:{L}=\:\frac{\mathrm{1}}{\mathrm{3}{n}}\:\underset{{u}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{{u}−\mathrm{1}}{\left(\frac{{u}^{\mathrm{9}} +\mathrm{6}}{\mathrm{7}}\right)−\mathrm{1}} \\ $$$$\:\:\:\:{L}=\frac{\mathrm{7}}{\mathrm{3}{n}}\:\underset{{u}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{{u}−\mathrm{1}}{{u}^{\mathrm{9}} −\mathrm{1}} \\ $$$$\:\:\:\:{L}=\:\frac{\mathrm{7}}{\mathrm{3}{n}}\:×\frac{\mathrm{1}}{\mathrm{9}}\:=\:\frac{\mathrm{7}}{\mathrm{27}{n}}\: \\ $$
Answered by qaz last updated on 26/Nov/21

$$\underset{\mathrm{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\sqrt[{\mathrm{9}}]{\mathrm{7x}−\mathrm{6}}−\mathrm{1}}{\mathrm{nx}^{\mathrm{3}} −\mathrm{n}}=\frac{\mathrm{1}}{\mathrm{n}}\underset{\mathrm{x}\rightarrow\mathrm{1},\xi\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\xi^{−\mathrm{8}/\mathrm{9}} \left(\mathrm{7x}−\mathrm{7}\right)}{\mathrm{9}\left(\mathrm{x}^{\mathrm{3}} −\mathrm{1}\right)}=\frac{\mathrm{7}}{\mathrm{9n}}\underset{\mathrm{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}=\frac{\mathrm{7}}{\mathrm{27n}} \\ $$
