Menu Close

Question-160270

Tinku Tara 0 Comments
Pin




Question Number 160270 by alf123 last updated on 27/Nov/21
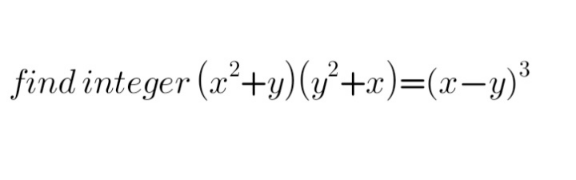
Answered by Rasheed.Sindhi last updated on 27/Nov/21
(x^2 +y)(y^2 +x)=(x−y)^3 ⇒ { ((x^2 +y=x−y_((i)) ∧ y^2 +x=(x−y)^2 _((ii)) )),(( OR)),((x^2 +y=(x−y)^2 _((iii)) ∧ y^2 +x=x−y_((iv)) )) :} ⇒ { (((ii)/(i): ((y^2 +x)/(x^2 +y))=x−y.....(v))),(( OR)),(((iii)/(iv): ((x^2 +y)/(y^2 +x))=x−y.....(vi))) :} From (v) & (vi): ((y^2 +x)/(x^2 +y))=((x^2 +y)/(y^2 +x))⇒(x^2 +y)^2 =(y^2 +x)^2 ⇒ { ((x^2 +y=y^2 +x⇒x^2 −y^2 +y−x=0)),((x^2 +y=−y^2 −x⇒x^2 +y^2 +y+x=0)) :} ⇒ { (((x−y)(x+y−1)=0⇒x=y ∣ x+y=1)),((x^2 +y^2 +y+x=0⇒(x,y)=(−1,−1),(0,0))) :} x=y ∣ y=1−x x=y 2(x^2 +x)=0 x(x+1)=0 x=0⇒y=0 x=−1,y=−1 y=1−x (x^2 +1−x)( (1−x)^2 +x )=(x−(1−x) )^3 (x^2 −x+1)(x^2 −x+1)=(2x−1)^3 x^2 −x+1=(2x−1)^1 =(2x−1)^2 ...A (2x−1)^1 =(2x−1)^2 suggest: 2x−1=0,1 { ((x=1/2 doesn′t obey fully A(All the three sides are not equal))),((x=1(✓)⇒y=1−1=0)) :} x=1,y=0 (x,y)=(0,0),(−1,−1),(1,0)
$$\left({x}^{\mathrm{2}} +{y}\right)\left({y}^{\mathrm{2}} +{x}\right)=\left({x}−{y}\right)^{\mathrm{3}} \\ $$$$\Rightarrow\begin{cases}{\underset{\left({i}\right)} {\underbrace{{x}^{\mathrm{2}} +{y}={x}−{y}}}\:\wedge\underset{\left({ii}\right)} {\underbrace{\:{y}^{\mathrm{2}} +{x}=\left({x}−{y}\right)^{\mathrm{2}} }}}\\{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{OR}}\\{\underset{\left({iii}\right)} {\underbrace{{x}^{\mathrm{2}} +{y}=\left({x}−{y}\right)^{\mathrm{2}} }}\:\wedge\:\underset{\left({iv}\right)} {\underbrace{{y}^{\mathrm{2}} +{x}={x}−{y}}}}\end{cases} \\ $$$$\Rightarrow\begin{cases}{\left({ii}\right)/\left({i}\right):\:\:\frac{{y}^{\mathrm{2}} +{x}}{{x}^{\mathrm{2}} +{y}}={x}−{y}…..\left({v}\right)}\\{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{OR}}\\{\left({iii}\right)/\left({iv}\right):\:\:\frac{{x}^{\mathrm{2}} +{y}}{{y}^{\mathrm{2}} +{x}}={x}−{y}…..\left({vi}\right)}\end{cases} \\ $$$${From}\:\left({v}\right)\:\&\:\left({vi}\right): \\ $$$$\frac{{y}^{\mathrm{2}} +{x}}{{x}^{\mathrm{2}} +{y}}=\frac{{x}^{\mathrm{2}} +{y}}{{y}^{\mathrm{2}} +{x}}\Rightarrow\left({x}^{\mathrm{2}} +{y}\right)^{\mathrm{2}} =\left({y}^{\mathrm{2}} +{x}\right)^{\mathrm{2}} \:\:\: \\ $$$$\Rightarrow\begin{cases}{{x}^{\mathrm{2}} +{y}={y}^{\mathrm{2}} +{x}\Rightarrow{x}^{\mathrm{2}} −{y}^{\mathrm{2}} +{y}−{x}=\mathrm{0}}\\{{x}^{\mathrm{2}} +{y}=−{y}^{\mathrm{2}} −{x}\Rightarrow{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{y}+{x}=\mathrm{0}}\end{cases} \\ $$$$\Rightarrow\begin{cases}{\left({x}−{y}\right)\left({x}+{y}−\mathrm{1}\right)=\mathrm{0}\Rightarrow{x}={y}\:\mid\:{x}+{y}=\mathrm{1}}\\{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{y}+{x}=\mathrm{0}\Rightarrow\left({x},{y}\right)=\left(−\mathrm{1},−\mathrm{1}\right),\left(\mathrm{0},\mathrm{0}\right)}\end{cases} \\ $$$${x}={y}\:\mid\:{y}=\mathrm{1}−{x} \\ $$$$\underline{{x}={y}} \\ $$$$\mathrm{2}\left({x}^{\mathrm{2}} +{x}\right)=\mathrm{0} \\ $$$${x}\left({x}+\mathrm{1}\right)=\mathrm{0} \\ $$$${x}=\mathrm{0}\Rightarrow{y}=\mathrm{0} \\ $$$${x}=−\mathrm{1},{y}=−\mathrm{1} \\ $$$$\underline{{y}=\mathrm{1}−{x}} \\ $$$$\left({x}^{\mathrm{2}} +\mathrm{1}−{x}\right)\left(\:\left(\mathrm{1}−{x}\right)^{\mathrm{2}} +{x}\:\right)=\left({x}−\left(\mathrm{1}−{x}\right)\:\right)^{\mathrm{3}} \\ $$$$\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)=\left(\mathrm{2}{x}−\mathrm{1}\right)^{\mathrm{3}} \\ $$$${x}^{\mathrm{2}} −{x}+\mathrm{1}=\left(\mathrm{2}{x}−\mathrm{1}\right)^{\mathrm{1}} =\left(\mathrm{2}{x}−\mathrm{1}\right)^{\mathrm{2}} …{A} \\ $$$$\left(\mathrm{2}{x}−\mathrm{1}\right)^{\mathrm{1}} =\left(\mathrm{2}{x}−\mathrm{1}\right)^{\mathrm{2}} \:{suggest}: \\ $$$$\:\:\:\mathrm{2}{x}−\mathrm{1}=\mathrm{0},\mathrm{1} \\ $$$$\begin{cases}{{x}=\mathrm{1}/\mathrm{2}\:{doesn}'{t}\:{obey}\:{fully}\:{A}\left({All}\:{the}\:{three}\:{sides}\:{are}\:{not}\:{equal}\right)}\\{{x}=\mathrm{1}\left(\checkmark\right)\Rightarrow{y}=\mathrm{1}−\mathrm{1}=\mathrm{0}}\end{cases} \\ $$$${x}=\mathrm{1},{y}=\mathrm{0} \\ $$$$\: \\ $$$$\:\left({x},{y}\right)=\left(\mathrm{0},\mathrm{0}\right),\left(−\mathrm{1},−\mathrm{1}\right),\left(\mathrm{1},\mathrm{0}\right) \\ $$
Commented by mr W last updated on 27/Nov/21
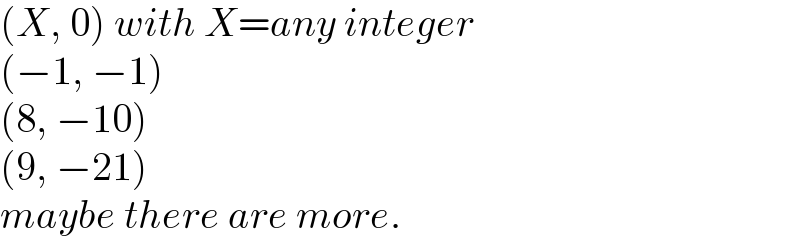
(X, 0) with X=any integer (−1, −1) (8, −10) (9, −21) maybe there are more.
$$\left({X},\:\mathrm{0}\right)\:{with}\:{X}={any}\:{integer} \\ $$$$\left(−\mathrm{1},\:−\mathrm{1}\right) \\ $$$$\left(\mathrm{8},\:−\mathrm{10}\right) \\ $$$$\left(\mathrm{9},\:−\mathrm{21}\right) \\ $$$${maybe}\:{there}\:{are}\:{more}. \\ $$
Commented by Rasheed.Sindhi last updated on 27/Nov/21
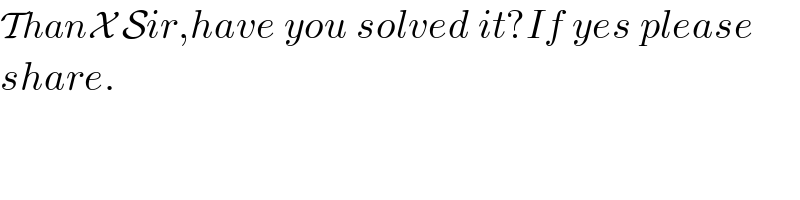
ThanX Sir,have you solved it?If yes please share.
$$\mathcal{T}{han}\mathcal{X}\:\mathcal{S}{ir},{have}\:{you}\:{solved}\:{it}?{If}\:{yes}\:{please} \\ $$$${share}. \\ $$
Answered by mr W last updated on 27/Nov/21
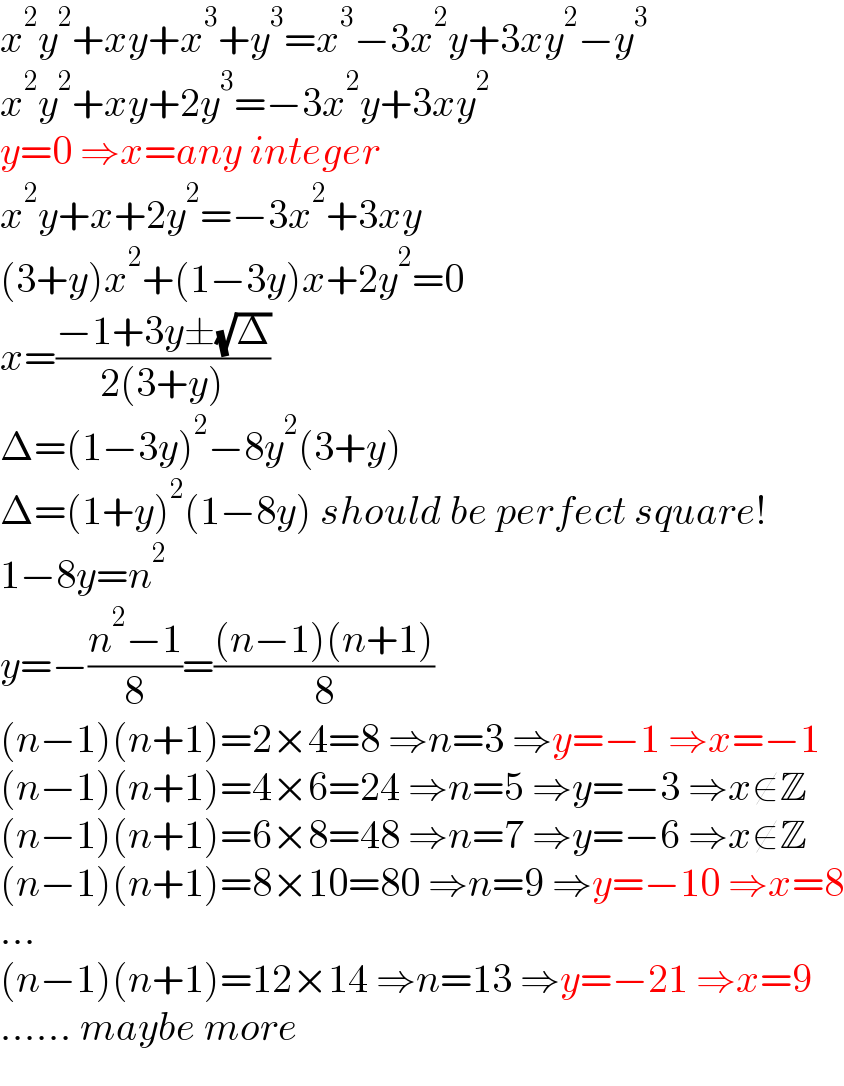
x^2 y^2 +xy+x^3 +y^3 =x^3 −3x^2 y+3xy^2 −y^3 x^2 y^2 +xy+2y^3 =−3x^2 y+3xy^2 y=0 ⇒x=any integer x^2 y+x+2y^2 =−3x^2 +3xy (3+y)x^2 +(1−3y)x+2y^2 =0 x=((−1+3y±(√Δ))/(2(3+y))) Δ=(1−3y)^2 −8y^2 (3+y) Δ=(1+y)^2 (1−8y) should be perfect square! 1−8y=n^2 y=−((n^2 −1)/8)=(((n−1)(n+1))/8) (n−1)(n+1)=2×4=8 ⇒n=3 ⇒y=−1 ⇒x=−1 (n−1)(n+1)=4×6=24 ⇒n=5 ⇒y=−3 ⇒x∉Z (n−1)(n+1)=6×8=48 ⇒n=7 ⇒y=−6 ⇒x∉Z (n−1)(n+1)=8×10=80 ⇒n=9 ⇒y=−10 ⇒x=8 ... (n−1)(n+1)=12×14 ⇒n=13 ⇒y=−21 ⇒x=9 ...... maybe more
$${x}^{\mathrm{2}} {y}^{\mathrm{2}} +{xy}+{x}^{\mathrm{3}} +{y}^{\mathrm{3}} ={x}^{\mathrm{3}} −\mathrm{3}{x}^{\mathrm{2}} {y}+\mathrm{3}{xy}^{\mathrm{2}} −{y}^{\mathrm{3}} \\ $$$${x}^{\mathrm{2}} {y}^{\mathrm{2}} +{xy}+\mathrm{2}{y}^{\mathrm{3}} =−\mathrm{3}{x}^{\mathrm{2}} {y}+\mathrm{3}{xy}^{\mathrm{2}} \\ $$$${y}=\mathrm{0}\:\Rightarrow{x}={any}\:{integer} \\ $$$${x}^{\mathrm{2}} {y}+{x}+\mathrm{2}{y}^{\mathrm{2}} =−\mathrm{3}{x}^{\mathrm{2}} +\mathrm{3}{xy} \\ $$$$\left(\mathrm{3}+{y}\right){x}^{\mathrm{2}} +\left(\mathrm{1}−\mathrm{3}{y}\right){x}+\mathrm{2}{y}^{\mathrm{2}} =\mathrm{0} \\ $$$${x}=\frac{−\mathrm{1}+\mathrm{3}{y}\pm\sqrt{\Delta}}{\mathrm{2}\left(\mathrm{3}+{y}\right)} \\ $$$$\Delta=\left(\mathrm{1}−\mathrm{3}{y}\right)^{\mathrm{2}} −\mathrm{8}{y}^{\mathrm{2}} \left(\mathrm{3}+{y}\right) \\ $$$$\Delta=\left(\mathrm{1}+{y}\right)^{\mathrm{2}} \left(\mathrm{1}−\mathrm{8}{y}\right)\:{should}\:{be}\:{perfect}\:{square}! \\ $$$$\mathrm{1}−\mathrm{8}{y}={n}^{\mathrm{2}} \\ $$$${y}=−\frac{{n}^{\mathrm{2}} −\mathrm{1}}{\mathrm{8}}=\frac{\left({n}−\mathrm{1}\right)\left({n}+\mathrm{1}\right)}{\mathrm{8}} \\ $$$$\left({n}−\mathrm{1}\right)\left({n}+\mathrm{1}\right)=\mathrm{2}×\mathrm{4}=\mathrm{8}\:\Rightarrow{n}=\mathrm{3}\:\Rightarrow{y}=−\mathrm{1}\:\Rightarrow{x}=−\mathrm{1} \\ $$$$\left({n}−\mathrm{1}\right)\left({n}+\mathrm{1}\right)=\mathrm{4}×\mathrm{6}=\mathrm{24}\:\Rightarrow{n}=\mathrm{5}\:\Rightarrow{y}=−\mathrm{3}\:\Rightarrow{x}\notin\mathbb{Z} \\ $$$$\left({n}−\mathrm{1}\right)\left({n}+\mathrm{1}\right)=\mathrm{6}×\mathrm{8}=\mathrm{48}\:\Rightarrow{n}=\mathrm{7}\:\Rightarrow{y}=−\mathrm{6}\:\Rightarrow{x}\notin\mathbb{Z} \\ $$$$\left({n}−\mathrm{1}\right)\left({n}+\mathrm{1}\right)=\mathrm{8}×\mathrm{10}=\mathrm{80}\:\Rightarrow{n}=\mathrm{9}\:\Rightarrow{y}=−\mathrm{10}\:\Rightarrow{x}=\mathrm{8} \\ $$$$… \\ $$$$\left({n}−\mathrm{1}\right)\left({n}+\mathrm{1}\right)=\mathrm{12}×\mathrm{14}\:\Rightarrow{n}=\mathrm{13}\:\Rightarrow{y}=−\mathrm{21}\:\Rightarrow{x}=\mathrm{9} \\ $$$$……\:{maybe}\:{more} \\ $$
Commented by Rasheed.Sindhi last updated on 27/Nov/21
Wonderful Sir!
$$\mathcal{W}{onderful}\:\mathcal{S}{ir}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *