Question Number 160342 by alf123 last updated on 28/Nov/21

Answered by Rasheed.Sindhi last updated on 28/Nov/21
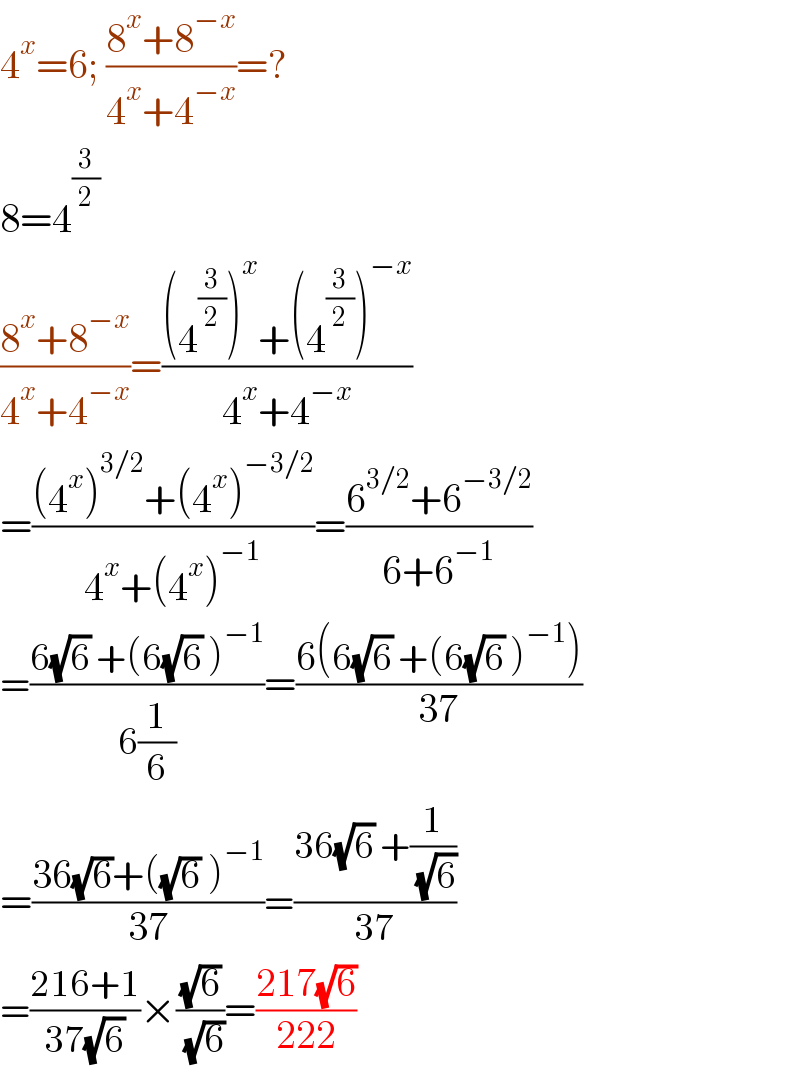
$$\mathrm{4}^{{x}} =\mathrm{6};\:\frac{\mathrm{8}^{{x}} +\mathrm{8}^{−{x}} }{\mathrm{4}^{{x}} +\mathrm{4}^{−{x}} }=? \\ $$$$\mathrm{8}=\mathrm{4}^{\frac{\mathrm{3}}{\mathrm{2}}} \\ $$$$\frac{\mathrm{8}^{{x}} +\mathrm{8}^{−{x}} }{\mathrm{4}^{{x}} +\mathrm{4}^{−{x}} }=\frac{\left(\mathrm{4}^{\frac{\mathrm{3}}{\mathrm{2}}} \right)^{{x}} +\left(\mathrm{4}^{\frac{\mathrm{3}}{\mathrm{2}}} \right)^{−{x}} }{\mathrm{4}^{{x}} +\mathrm{4}^{−{x}} } \\ $$$$=\frac{\left(\mathrm{4}^{{x}} \right)^{\mathrm{3}/\mathrm{2}} +\left(\mathrm{4}^{{x}} \right)^{−\mathrm{3}/\mathrm{2}} }{\mathrm{4}^{{x}} +\left(\mathrm{4}^{{x}} \right)^{−\mathrm{1}} }=\frac{\mathrm{6}^{\mathrm{3}/\mathrm{2}} +\mathrm{6}^{−\mathrm{3}/\mathrm{2}} }{\mathrm{6}+\mathrm{6}^{−\mathrm{1}} } \\ $$$$=\frac{\mathrm{6}\sqrt{\mathrm{6}}\:+\left(\mathrm{6}\sqrt{\mathrm{6}}\:\right)^{−\mathrm{1}} }{\mathrm{6}\frac{\mathrm{1}}{\mathrm{6}}}=\frac{\mathrm{6}\left(\mathrm{6}\sqrt{\mathrm{6}}\:+\left(\mathrm{6}\sqrt{\mathrm{6}}\:\right)^{−\mathrm{1}} \right)}{\mathrm{37}} \\ $$$$=\frac{\mathrm{36}\sqrt{\mathrm{6}}+\left(\sqrt{\mathrm{6}}\:\right)^{−\mathrm{1}} }{\mathrm{37}}=\frac{\mathrm{36}\sqrt{\mathrm{6}}\:+\frac{\mathrm{1}}{\:\sqrt{\mathrm{6}}}}{\mathrm{37}} \\ $$$$=\frac{\mathrm{216}+\mathrm{1}}{\mathrm{37}\sqrt{\mathrm{6}}}×\frac{\sqrt{\mathrm{6}}}{\:\sqrt{\mathrm{6}}}=\frac{\mathrm{217}\sqrt{\mathrm{6}}}{\mathrm{222}} \\ $$
Commented by MJS_new last updated on 28/Nov/21

$$\mathrm{good}! \\ $$$$…=\frac{\mathrm{217}\sqrt{\mathrm{6}}}{\mathrm{222}} \\ $$
Commented by Rasheed.Sindhi last updated on 28/Nov/21

$$\mathbb{T}\mathrm{han}\Bbbk\mathrm{s}\:\mathrm{sir}! \\ $$$${I}'{ve}\:{simplified}\:{now}. \\ $$
