Question Number 160473 by quvonnn last updated on 30/Nov/21

Answered by Rasheed.Sindhi last updated on 30/Nov/21
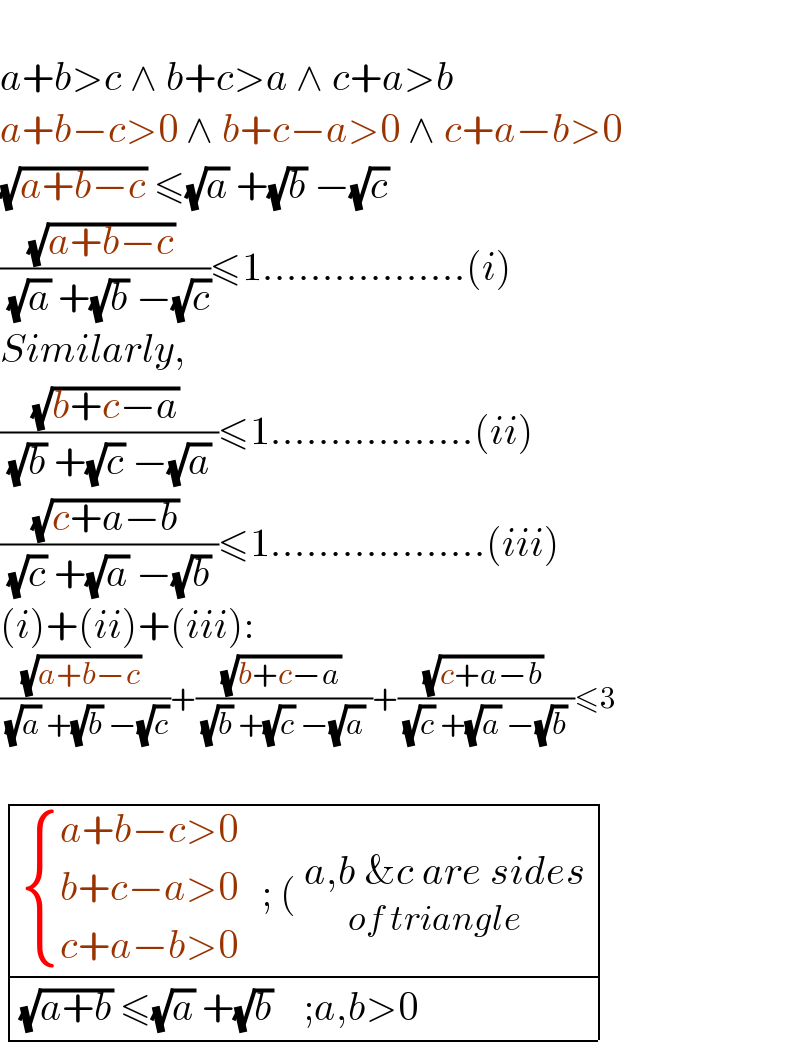
$$ \\ $$$${a}+{b}>{c}\:\wedge\:{b}+{c}>{a}\:\wedge\:{c}+{a}>{b} \\ $$$${a}+{b}−{c}>\mathrm{0}\:\wedge\:{b}+{c}−{a}>\mathrm{0}\:\wedge\:{c}+{a}−{b}>\mathrm{0} \\ $$$$\sqrt{{a}+{b}−{c}}\:\leqslant\sqrt{{a}}\:+\sqrt{{b}}\:−\sqrt{{c}} \\ $$$$\frac{\sqrt{{a}+{b}−{c}}\:}{\:\sqrt{{a}}\:+\sqrt{{b}}\:−\sqrt{{c}}}\leqslant\mathrm{1}……………..\left({i}\right) \\ $$$${Similarly}, \\ $$$$\frac{\sqrt{{b}+{c}−{a}}\:}{\:\sqrt{{b}}\:+\sqrt{{c}}\:−\sqrt{{a}}\:}\leqslant\mathrm{1}……………..\left({ii}\right) \\ $$$$\frac{\sqrt{{c}+{a}−{b}}\:}{\:\sqrt{{c}}\:+\sqrt{{a}}\:−\sqrt{{b}}\:}\leqslant\mathrm{1}………………\left({iii}\right) \\ $$$$\left({i}\right)+\left({ii}\right)+\left({iii}\right): \\ $$$$\frac{\sqrt{{a}+{b}−{c}}\:}{\:\sqrt{{a}}\:+\sqrt{{b}}\:−\sqrt{{c}}}+\frac{\sqrt{{b}+{c}−{a}}\:}{\:\sqrt{{b}}\:+\sqrt{{c}}\:−\sqrt{{a}}\:}+\frac{\sqrt{{c}+{a}−{b}}\:}{\:\sqrt{{c}}\:+\sqrt{{a}}\:−\sqrt{{b}}\:}\leqslant\mathrm{3} \\ $$$$ \\ $$$$\begin{array}{|c|c|}{\begin{cases}{{a}+{b}−{c}>\mathrm{0}}\\{{b}+{c}−{a}>\mathrm{0}}\\{{c}+{a}−{b}>\mathrm{0}}\end{cases}\:\:\:;\:\left(_{\:\:\:\:\:\:\:\:\:\:\:\:\:{of}\:{triangle}} ^{\:{a},{b}\:\&{c}\:{are}\:{sides}} \right.}\\{\sqrt{{a}+{b}}\:\leqslant\sqrt{{a}}\:+\sqrt{{b}}\:\:\:\:;{a},{b}>\mathrm{0}\:}\\\hline\end{array} \\ $$
