Menu Close

Question-160487

Tinku Tara 0 Comments
Pin




Question Number 160487 by HongKing last updated on 30/Nov/21
Answered by Rasheed.Sindhi last updated on 30/Nov/21
(10a+b)+(10b+a)=10c+3 11a+11b=10c+3 11(a+b)=10c+3..............(i) 11∣ 10c+3⇒10c+3=33⇒c=3 (2-digit multiple of 11 with unit 3 is only 33) (i)⇒a+b=((10c+3)/(11))=((33)/(11))=3 a+b+2c=3+2(3)=9
$$\left(\mathrm{10}{a}+{b}\right)+\left(\mathrm{10}{b}+{a}\right)=\mathrm{10}{c}+\mathrm{3} \\ $$$$\mathrm{11}{a}+\mathrm{11}{b}=\mathrm{10}{c}+\mathrm{3} \\ $$$$\mathrm{11}\left({a}+{b}\right)=\mathrm{10}{c}+\mathrm{3}…………..\left({i}\right) \\ $$$$\mathrm{11}\mid\:\mathrm{10}{c}+\mathrm{3}\Rightarrow\mathrm{10}{c}+\mathrm{3}=\mathrm{33}\Rightarrow{c}=\mathrm{3} \\ $$$$\left(\mathrm{2}-{digit}\:{multiple}\:{of}\:\mathrm{11}\:{with}\:{unit}\:\mathrm{3}\right. \\ $$$$\left.{is}\:{only}\:\mathrm{33}\right) \\ $$$$ \\ $$$$\left({i}\right)\Rightarrow{a}+{b}=\frac{\mathrm{10}{c}+\mathrm{3}}{\mathrm{11}}=\frac{\mathrm{33}}{\mathrm{11}}=\mathrm{3} \\ $$$${a}+{b}+\mathrm{2}{c}=\mathrm{3}+\mathrm{2}\left(\mathrm{3}\right)=\mathrm{9} \\ $$
Answered by Rasheed.Sindhi last updated on 30/Nov/21
AnOther Road to Rome ab^(−) +ba^(−) =c3^(−) ; a+b+2c=? ab^(−) +ba^(−) =c3^(−) ⇒sum of units: a+b=3 or13 a+b=3 (no carry) sum of tens:a+b=c=3 a+b+2c=3+2(3)=9 a+b=13(1 carry) a+b+1=c⇒c=13+1=14 but c≤9 ∴ a+b≠13 Hence a+b=3=c a+b+2c=3+2(3)=9
$$\mathbb{A}\mathrm{n}\mathbb{O}\mathrm{ther}\:\mathbb{R}\mathrm{oad}\:\mathrm{to}\:\mathbb{R}\mathrm{ome} \\ $$$$\overline {\mathrm{ab}}+\overline {\mathrm{ba}}=\overline {\mathrm{c3}}\:;\:\mathrm{a}+\mathrm{b}+\mathrm{2c}=? \\ $$$$\overline {\mathrm{ab}}+\overline {\mathrm{ba}}=\overline {\mathrm{c3}}\Rightarrow\mathrm{sum}\:\mathrm{of}\:\mathrm{units}:\:\mathrm{a}+\mathrm{b}=\mathrm{3}\:\mathrm{or13}\: \\ $$$$\underline{\mathrm{a}+\mathrm{b}=\mathrm{3}}\:\left(\mathrm{no}\:\mathrm{carry}\right) \\ $$$$\mathrm{sum}\:\mathrm{of}\:\mathrm{tens}:\mathrm{a}+\mathrm{b}=\mathrm{c}=\mathrm{3}\: \\ $$$$\mathrm{a}+\mathrm{b}+\mathrm{2c}=\mathrm{3}+\mathrm{2}\left(\mathrm{3}\right)=\mathrm{9} \\ $$$$\underline{\mathrm{a}+\mathrm{b}=\mathrm{13}}\left(\mathrm{1}\:\mathrm{carry}\right) \\ $$$$\mathrm{a}+\mathrm{b}+\mathrm{1}=\mathrm{c}\Rightarrow\mathrm{c}=\mathrm{13}+\mathrm{1}=\mathrm{14}\:\mathrm{but}\:\mathrm{c}\leqslant\mathrm{9} \\ $$$$\therefore\:\mathrm{a}+\mathrm{b}\neq\mathrm{13} \\ $$$$\mathcal{H}{ence}\:\mathrm{a}+\mathrm{b}=\mathrm{3}=\mathrm{c} \\ $$$$\mathrm{a}+\mathrm{b}+\mathrm{2c}=\mathrm{3}+\mathrm{2}\left(\mathrm{3}\right)=\mathrm{9} \\ $$
Answered by Rasheed.Sindhi last updated on 30/Nov/21
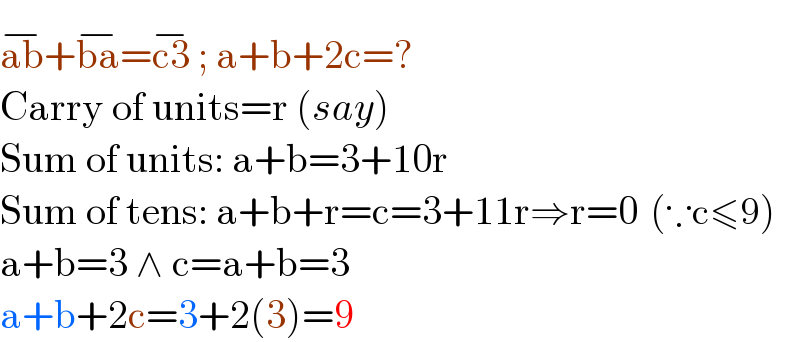
ab^(−) +ba^(−) =c3^(−) ; a+b+2c=? Carry of units=r (say) Sum of units: a+b=3+10r Sum of tens: a+b+r=c=3+11r⇒r=0 (∵c≤9) a+b=3 ∧ c=a+b=3 a+b+2c=3+2(3)=9
$$\overline {\mathrm{ab}}+\overline {\mathrm{ba}}=\overline {\mathrm{c3}}\:;\:\mathrm{a}+\mathrm{b}+\mathrm{2c}=? \\ $$$$\mathrm{Carry}\:\mathrm{of}\:\mathrm{units}=\mathrm{r}\:\left({say}\right) \\ $$$$\mathrm{Sum}\:\mathrm{of}\:\mathrm{units}:\:\mathrm{a}+\mathrm{b}=\mathrm{3}+\mathrm{10r} \\ $$$$\mathrm{Sum}\:\mathrm{of}\:\mathrm{tens}:\:\mathrm{a}+\mathrm{b}+\mathrm{r}=\mathrm{c}=\mathrm{3}+\mathrm{11r}\Rightarrow\mathrm{r}=\mathrm{0}\:\:\left(\because\mathrm{c}\leqslant\mathrm{9}\right) \\ $$$$\mathrm{a}+\mathrm{b}=\mathrm{3}\:\wedge\:\mathrm{c}=\mathrm{a}+\mathrm{b}=\mathrm{3} \\ $$$$\mathrm{a}+\mathrm{b}+\mathrm{2c}=\mathrm{3}+\mathrm{2}\left(\mathrm{3}\right)=\mathrm{9} \\ $$
Commented by HongKing last updated on 30/Nov/21
very nice my dear Sir thank you
$$\mathrm{very}\:\mathrm{nice}\:\mathrm{my}\:\mathrm{dear}\:\mathrm{Sir}\:\mathrm{thank}\:\mathrm{you} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *