Question Number 160522 by mnjuly1970 last updated on 01/Dec/21

Answered by mr W last updated on 03/Dec/21

Commented by mr W last updated on 03/Dec/21

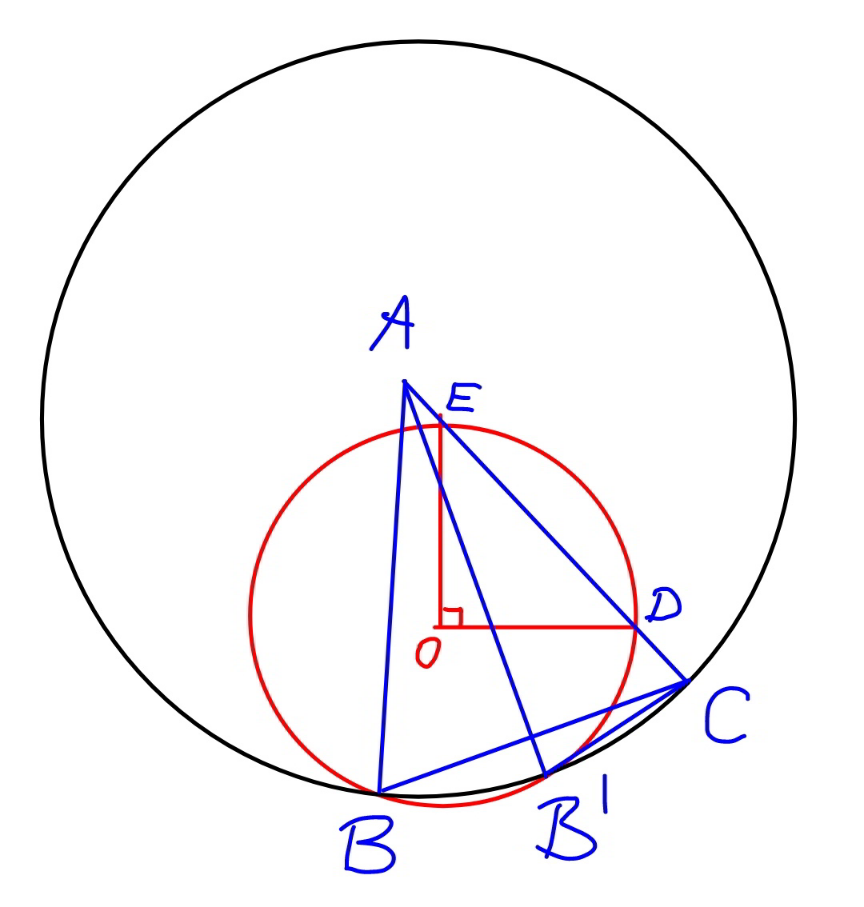
$${BE}^{\mathrm{2}} =\mathrm{25}^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} −\mathrm{2}×\mathrm{25}×\mathrm{3}\:\mathrm{cos}\:\left(\pi−\mathrm{2}\alpha\right) \\ $$$${BE}^{\mathrm{2}} =\mathrm{634}+\mathrm{150}\:\mathrm{cos}\:\left(\mathrm{2}\alpha\right) \\ $$$${BE}^{\mathrm{2}} =\mathrm{484}+\mathrm{300}\:\mathrm{cos}^{\mathrm{2}} \:\alpha \\ $$$$ \\ $$$${BC}=\mathrm{2}×\mathrm{25}\:\mathrm{cos}\:\alpha=\mathrm{50}\:\mathrm{cos}\:\alpha \\ $$$$ \\ $$$${BD}^{\mathrm{2}} =\mathrm{5}^{\mathrm{2}} +\left(\mathrm{50}\:\mathrm{cos}\:\alpha\right)^{\mathrm{2}} −\mathrm{2}×\mathrm{5}×\mathrm{50}\:\mathrm{cos}\:\alpha\:\mathrm{cos}\:\alpha\: \\ $$$${BD}^{\mathrm{2}} =\mathrm{25}+\mathrm{2000}\:\mathrm{cos}^{\mathrm{2}} \:\alpha \\ $$$$ \\ $$$${ED}^{\mathrm{2}} ={BE}^{\mathrm{2}} +{BD}^{\mathrm{2}} −\mathrm{2}×{BE}×{BD}\:\mathrm{cos}\:\mathrm{45}° \\ $$$$\mathrm{17}^{\mathrm{2}} =\mathrm{484}+\mathrm{300}\:\mathrm{cos}^{\mathrm{2}} \:\alpha+\mathrm{25}+\mathrm{2000}\:\mathrm{cos}^{\mathrm{2}} \:\alpha−\sqrt{\mathrm{2}\left(\mathrm{484}+\mathrm{300}\:\mathrm{cos}^{\mathrm{2}} \:\alpha\right)\left(\mathrm{25}+\mathrm{2000}\:\mathrm{cos}^{\mathrm{2}} \:\alpha\right)} \\ $$$$\mathrm{220}+\mathrm{2300}\:\mathrm{cos}^{\mathrm{2}} \:\alpha=\sqrt{\mathrm{2}\left(\mathrm{484}+\mathrm{300}\:\mathrm{cos}^{\mathrm{2}} \:\alpha\right)\left(\mathrm{25}+\mathrm{2000}\:\mathrm{cos}^{\mathrm{2}} \:\alpha\right)} \\ $$$$\mathrm{220}^{\mathrm{2}} +\mathrm{2300}^{\mathrm{2}} \:\mathrm{cos}^{\mathrm{4}} \:\alpha+\mathrm{2}×\mathrm{220}×\mathrm{2300}\:\mathrm{cos}^{\mathrm{2}} \:\alpha=\mathrm{2}×\mathrm{484}×\mathrm{25}+\mathrm{2}×\left(\mathrm{300}×\mathrm{25}+\mathrm{484}×\mathrm{2000}\right)\:\mathrm{cos}^{\mathrm{2}} \:\alpha+\mathrm{2}×\mathrm{300}×\mathrm{2000}\:\mathrm{cos}^{\mathrm{4}} \:\alpha \\ $$$$\mathrm{20450}\:\mathrm{cos}^{\mathrm{4}} \:\alpha−\mathrm{4695}\:\mathrm{cos}^{\mathrm{2}} \:\alpha+\mathrm{121}=\mathrm{0} \\ $$$$\mathrm{cos}^{\mathrm{2}} \:\alpha=\frac{\mathrm{4695}\pm\sqrt{\mathrm{4695}^{\mathrm{2}} −\mathrm{4}×\mathrm{20450}×\mathrm{121}}}{\mathrm{2}×\mathrm{20450}}=\frac{\mathrm{1}}{\mathrm{5}},\frac{\mathrm{121}}{\mathrm{4090}} \\ $$$$\mathrm{tan}\:\alpha=\sqrt{\frac{\mathrm{1}}{\mathrm{cos}^{\mathrm{2}} \:\alpha}−\mathrm{1}}=\sqrt{\mathrm{5}−\mathrm{1}}=\mathrm{2}\: \\ $$$$\mathrm{tan}\:\alpha=\sqrt{\frac{\mathrm{4090}}{\mathrm{121}}−\mathrm{1}}=\frac{\mathrm{63}}{\mathrm{11}}\: \\ $$$$ \\ $$$$\alpha=\mathrm{tan}^{−\mathrm{1}} \mathrm{2}\approx\mathrm{63}.\mathrm{435}°,\:\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{63}}{\mathrm{11}}\approx\mathrm{80}.\mathrm{956}° \\ $$
Commented by mr W last updated on 04/Dec/21
Commented by mr W last updated on 04/Dec/21
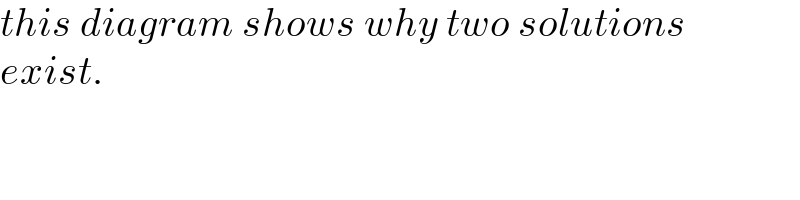
$${this}\:{diagram}\:{shows}\:{why}\:{two}\:{solutions} \\ $$$${exist}. \\ $$
