Question Number 160576 by mnjuly1970 last updated on 02/Dec/21

Commented by aleks041103 last updated on 02/Dec/21
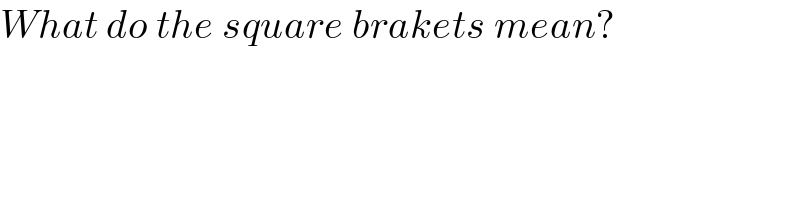
$${What}\:{do}\:{the}\:{square}\:{brakets}\:{mean}? \\ $$
Commented by mnjuly1970 last updated on 04/Dec/21
![[x]= ⌊x⌋](https://www.tinkutara.com/question/Q160670.png)
$$\:\:\left[{x}\right]=\:\lfloor{x}\rfloor \\ $$
Answered by aleks041103 last updated on 04/Dec/21
![ne^(−x) is a monotonously decreasing function. [ne^(−x) ]=k⇔ne^(−x) ∈[k,k+1)⇔e^x ∈((n/(k+1)),(n/k)] ⇒x∈(ln(n)−ln(k+1),ln(n)−ln(k)] x∈[0,∞)⇒ln(n)≥ln(k+1)⇒k≤n−1 ⇒∫_0 ^∞ [ne^(−x) ]dx=Σ_(k=0) ^(n−1) k ln(1+(1/k))= =Σ_(k=1) ^(n−1) k ln(1+(1/k)) ⇒L=lim_(n→∞) (√n) e^((Σ_(k=1) ^(n−1) k ln(1+(1/k)))−n) e^((Σ_(k=1) ^(n−1) k ln(1+(1/k)))−n) =e^(−n) Π_(k=1) ^(n−1) (((k+1)^k )/k^k ) Π_(k=1) ^(n−1) (((k+1)^k )/k^k )=Π_(k=1) ^(n−1) (((k+1)^(k+1) )/k^k )Π_(k=1) ^(n−1) (1/(k+1))= =(n^n /(n!)) ⇒L=lim_(n→∞) (((√n)n^n e^(−n) )/(n!)) Stirling approxition: n!∼(√(2πn))n^n e^(−n) ⇒L=lim_(n→∞) (((√n)n^n e^(−n) )/( (√(2πn))n^n e^(−n) ))= =(1/( (√(2π)))) ⇒L=(1/( (√(2π))))](https://www.tinkutara.com/question/Q160684.png)
$${ne}^{−{x}} \:{is}\:{a}\:{monotonously}\:{decreasing}\:{function}. \\ $$$$\left[{ne}^{−{x}} \right]={k}\Leftrightarrow{ne}^{−{x}} \in\left[{k},{k}+\mathrm{1}\right)\Leftrightarrow{e}^{{x}} \in\left(\frac{{n}}{{k}+\mathrm{1}},\frac{{n}}{{k}}\right] \\ $$$$\Rightarrow{x}\in\left({ln}\left({n}\right)−{ln}\left({k}+\mathrm{1}\right),{ln}\left({n}\right)−{ln}\left({k}\right)\right] \\ $$$${x}\in\left[\mathrm{0},\infty\right)\Rightarrow{ln}\left({n}\right)\geqslant{ln}\left({k}+\mathrm{1}\right)\Rightarrow{k}\leqslant{n}−\mathrm{1} \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\infty} \left[{ne}^{−{x}} \right]{dx}=\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}{k}\:{ln}\left(\mathrm{1}+\frac{\mathrm{1}}{{k}}\right)= \\ $$$$=\underset{{k}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\sum}}{k}\:{ln}\left(\mathrm{1}+\frac{\mathrm{1}}{{k}}\right) \\ $$$$\Rightarrow{L}=\underset{{n}\rightarrow\infty} {{lim}}\sqrt{{n}}\:{e}^{\left(\underset{{k}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\sum}}{k}\:{ln}\left(\mathrm{1}+\frac{\mathrm{1}}{{k}}\right)\right)−{n}} \\ $$$${e}^{\left(\underset{{k}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\sum}}{k}\:{ln}\left(\mathrm{1}+\frac{\mathrm{1}}{{k}}\right)\right)−{n}} ={e}^{−{n}} \underset{{k}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\prod}}\frac{\left({k}+\mathrm{1}\right)^{{k}} }{{k}^{{k}} } \\ $$$$\underset{{k}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\prod}}\frac{\left({k}+\mathrm{1}\right)^{{k}} }{{k}^{{k}} }=\underset{{k}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\prod}}\frac{\left({k}+\mathrm{1}\right)^{{k}+\mathrm{1}} }{{k}^{{k}} }\underset{{k}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\prod}}\frac{\mathrm{1}}{{k}+\mathrm{1}}= \\ $$$$=\frac{{n}^{{n}} }{{n}!} \\ $$$$\Rightarrow{L}=\underset{{n}\rightarrow\infty} {{lim}}\frac{\sqrt{{n}}{n}^{{n}} {e}^{−{n}} }{{n}!} \\ $$$${Stirling}\:{approxition}: \\ $$$${n}!\sim\sqrt{\mathrm{2}\pi{n}}{n}^{{n}} {e}^{−{n}} \\ $$$$\Rightarrow{L}=\underset{{n}\rightarrow\infty} {{lim}}\frac{\sqrt{{n}}{n}^{{n}} {e}^{−{n}} }{\:\sqrt{\mathrm{2}\pi{n}}{n}^{{n}} {e}^{−{n}} }= \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}\pi}} \\ $$$$\Rightarrow{L}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}\pi}} \\ $$
Commented by mnjuly1970 last updated on 04/Dec/21
$${thannk}\:{you}\:{so}\:{much}\:{sir} \\ $$
