Question Number 160618 by amin96 last updated on 03/Dec/21
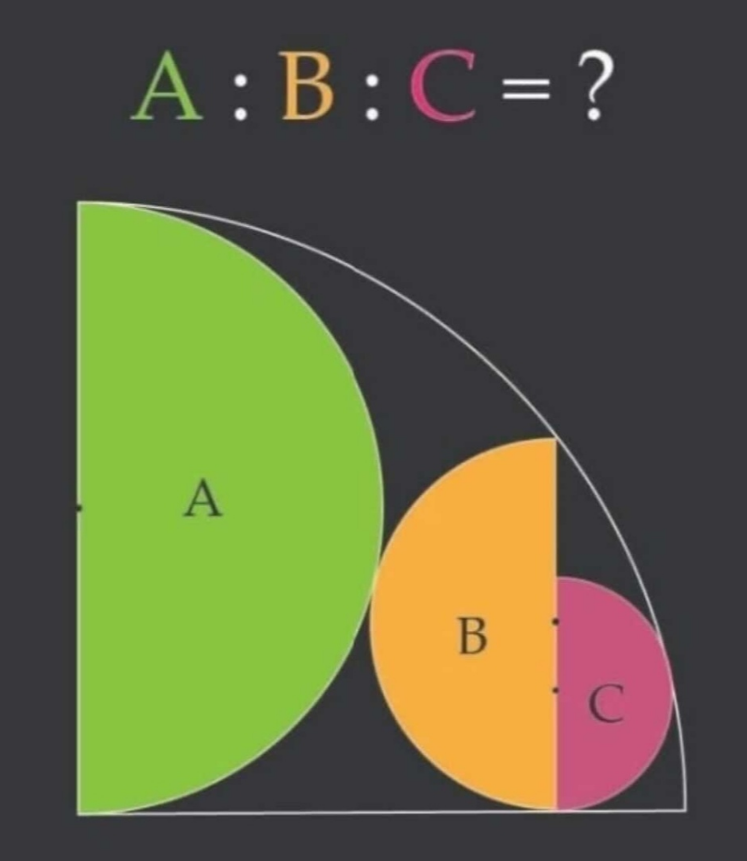
Answered by mr W last updated on 03/Dec/21
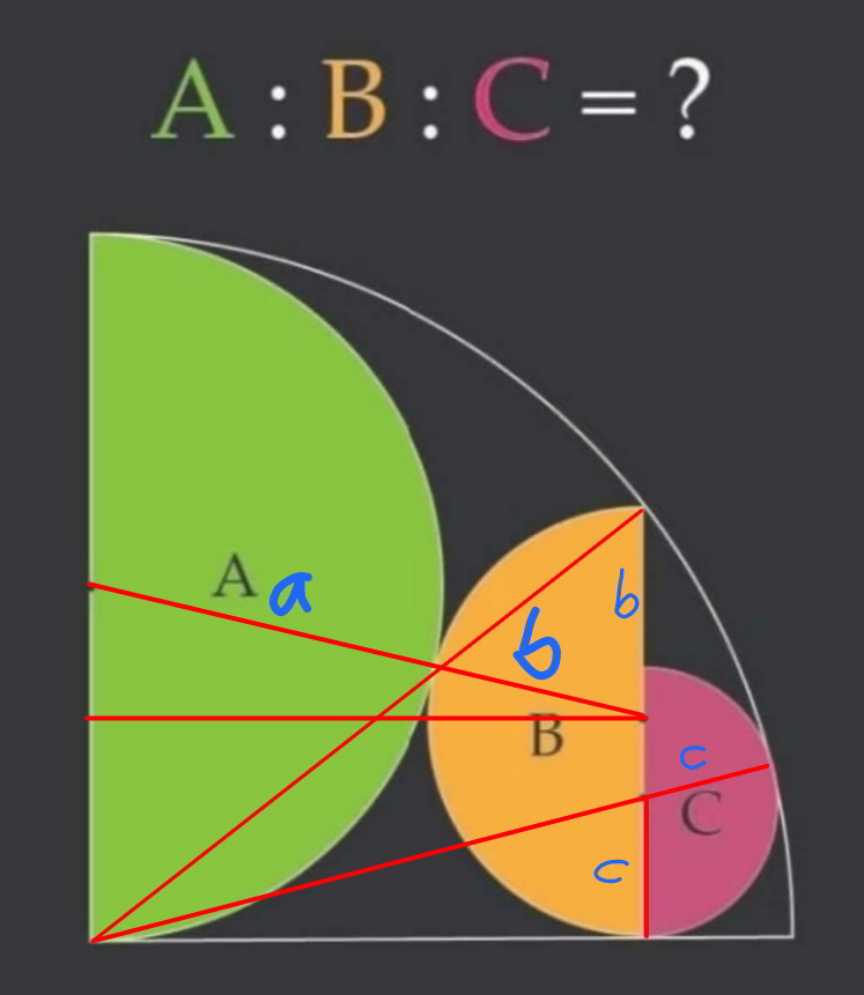
Commented by mr W last updated on 03/Dec/21
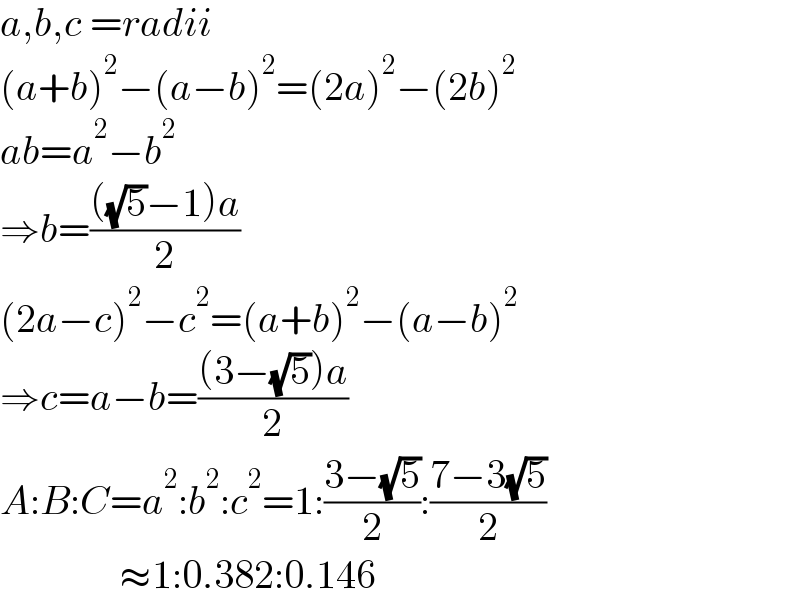
$${a},{b},{c}\:={radii} \\ $$$$\left({a}+{b}\right)^{\mathrm{2}} −\left({a}−{b}\right)^{\mathrm{2}} =\left(\mathrm{2}{a}\right)^{\mathrm{2}} −\left(\mathrm{2}{b}\right)^{\mathrm{2}} \\ $$$${ab}={a}^{\mathrm{2}} −{b}^{\mathrm{2}} \\ $$$$\Rightarrow{b}=\frac{\left(\sqrt{\mathrm{5}}−\mathrm{1}\right){a}}{\mathrm{2}} \\ $$$$\left(\mathrm{2}{a}−{c}\right)^{\mathrm{2}} −{c}^{\mathrm{2}} =\left({a}+{b}\right)^{\mathrm{2}} −\left({a}−{b}\right)^{\mathrm{2}} \\ $$$$\Rightarrow{c}={a}−{b}=\frac{\left(\mathrm{3}−\sqrt{\mathrm{5}}\right){a}}{\mathrm{2}} \\ $$$${A}:{B}:{C}={a}^{\mathrm{2}} :{b}^{\mathrm{2}} :{c}^{\mathrm{2}} =\mathrm{1}:\frac{\mathrm{3}−\sqrt{\mathrm{5}}}{\mathrm{2}}:\frac{\mathrm{7}−\mathrm{3}\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\approx\mathrm{1}:\mathrm{0}.\mathrm{382}:\mathrm{0}.\mathrm{146} \\ $$
Commented by Tawa11 last updated on 03/Dec/21

$$\mathrm{Great}\:\mathrm{sir} \\ $$
