Question Number 160747 by amin96 last updated on 05/Dec/21
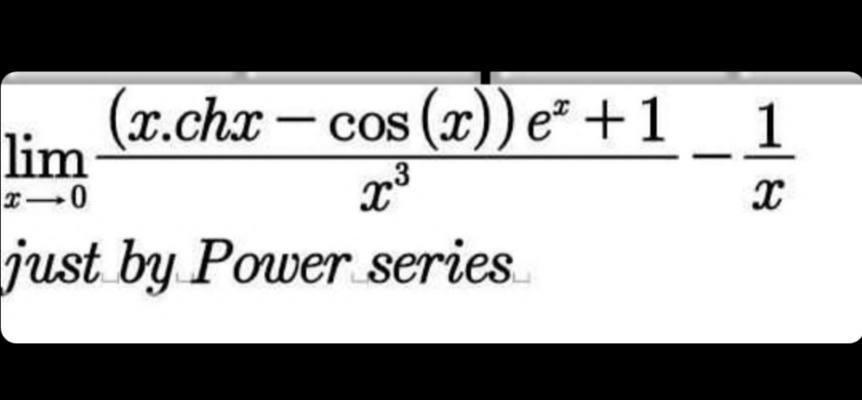
Commented by amin96 last updated on 05/Dec/21

$$ \\ $$does anyone have a solution?
Answered by qaz last updated on 06/Dec/21
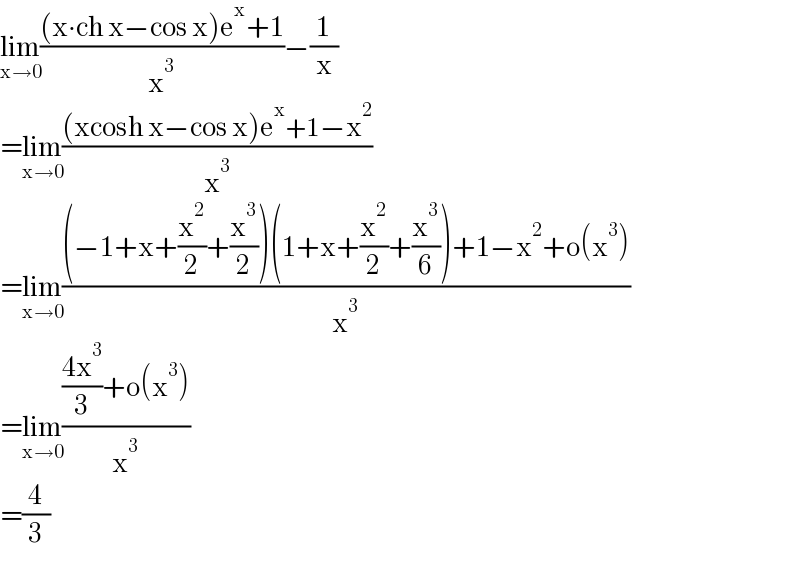
$$\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\mathrm{x}\centerdot\mathrm{ch}\:\mathrm{x}−\mathrm{cos}\:\mathrm{x}\right)\mathrm{e}^{\mathrm{x}} +\mathrm{1}}{\mathrm{x}^{\mathrm{3}} }−\frac{\mathrm{1}}{\mathrm{x}} \\ $$$$=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\mathrm{xcosh}\:\mathrm{x}−\mathrm{cos}\:\mathrm{x}\right)\mathrm{e}^{\mathrm{x}} +\mathrm{1}−\mathrm{x}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{3}} } \\ $$$$=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(−\mathrm{1}+\mathrm{x}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}+\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{2}}\right)\left(\mathrm{1}+\mathrm{x}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}+\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{6}}\right)+\mathrm{1}−\mathrm{x}^{\mathrm{2}} +\mathrm{o}\left(\mathrm{x}^{\mathrm{3}} \right)}{\mathrm{x}^{\mathrm{3}} } \\ $$$$=\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{\mathrm{4x}^{\mathrm{3}} }{\mathrm{3}}+\mathrm{o}\left(\mathrm{x}^{\mathrm{3}} \right)}{\mathrm{x}^{\mathrm{3}} } \\ $$$$=\frac{\mathrm{4}}{\mathrm{3}} \\ $$
