Question Number 160753 by Gbenga last updated on 05/Dec/21
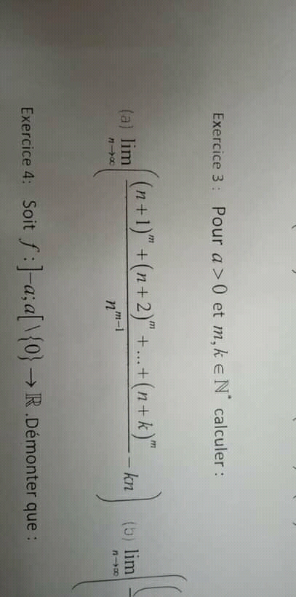
Commented by Tinku Tara last updated on 06/Dec/21
$$\mathrm{Please}\:\mathrm{rotate}\:\mathrm{image}\:\mathrm{before}\:\mathrm{uploading} \\ $$
Answered by qaz last updated on 06/Dec/21
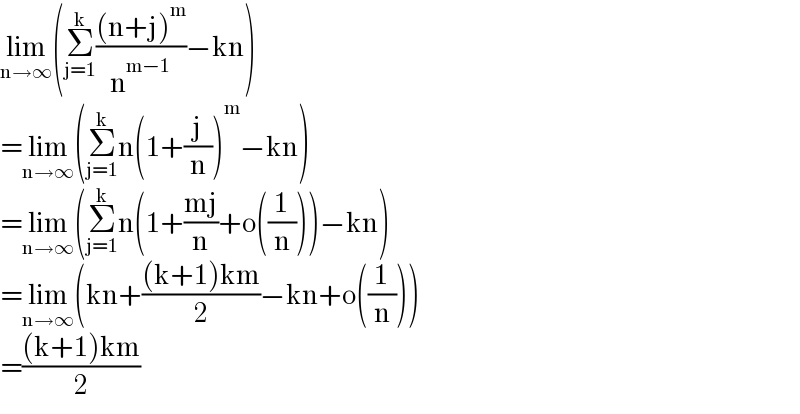
$$\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\left(\underset{\mathrm{j}=\mathrm{1}} {\overset{\mathrm{k}} {\sum}}\frac{\left(\mathrm{n}+\mathrm{j}\right)^{\mathrm{m}} }{\mathrm{n}^{\mathrm{m}−\mathrm{1}} }−\mathrm{kn}\right) \\ $$$$=\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\left(\underset{\mathrm{j}=\mathrm{1}} {\overset{\mathrm{k}} {\sum}}\mathrm{n}\left(\mathrm{1}+\frac{\mathrm{j}}{\mathrm{n}}\right)^{\mathrm{m}} −\mathrm{kn}\right) \\ $$$$=\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\left(\underset{\mathrm{j}=\mathrm{1}} {\overset{\mathrm{k}} {\sum}}\mathrm{n}\left(\mathrm{1}+\frac{\mathrm{mj}}{\mathrm{n}}+\mathrm{o}\left(\frac{\mathrm{1}}{\mathrm{n}}\right)\right)−\mathrm{kn}\right) \\ $$$$=\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{kn}+\frac{\left(\mathrm{k}+\mathrm{1}\right)\mathrm{km}}{\mathrm{2}}−\mathrm{kn}+\mathrm{o}\left(\frac{\mathrm{1}}{\mathrm{n}}\right)\right) \\ $$$$=\frac{\left(\mathrm{k}+\mathrm{1}\right)\mathrm{km}}{\mathrm{2}} \\ $$
