Question Number 160816 by 0731619 last updated on 07/Dec/21

Commented by mr W last updated on 07/Dec/21
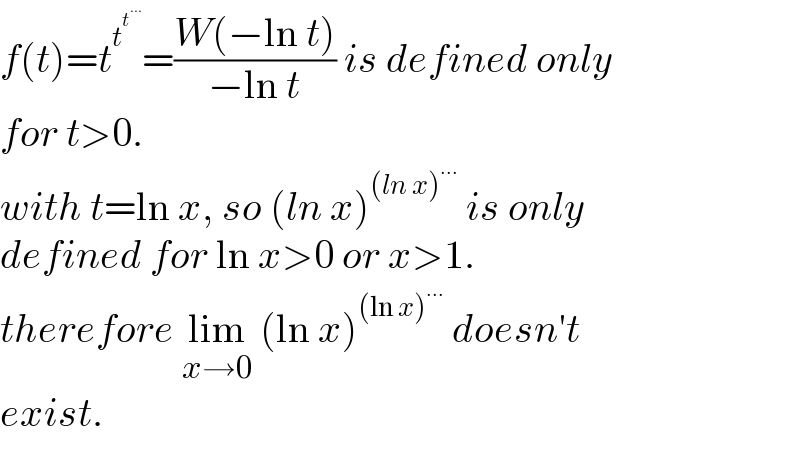
$${f}\left({t}\right)={t}^{{t}^{{t}^{…} } } =\frac{{W}\left(−\mathrm{ln}\:{t}\right)}{−\mathrm{ln}\:{t}}\:{is}\:{defined}\:{only} \\ $$$${for}\:{t}>\mathrm{0}. \\ $$$${with}\:{t}=\mathrm{ln}\:{x},\:{so}\:\left({ln}\:{x}\right)^{\left({ln}\:{x}\right)^{…} } \:{is}\:{only}\: \\ $$$${defined}\:{for}\:\mathrm{ln}\:{x}>\mathrm{0}\:{or}\:{x}>\mathrm{1}. \\ $$$${therefore}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\mathrm{ln}\:{x}\right)^{\left(\mathrm{ln}\:{x}\right)^{…} } \:{doesn}'{t} \\ $$$${exist}. \\ $$
