Question Number 160924 by amin96 last updated on 09/Dec/21

Commented by amin96 last updated on 09/Dec/21

$$ \\ $$green area=?
H orthogonal center
H orthogonal center
Answered by mr W last updated on 09/Dec/21

Commented by mr W last updated on 09/Dec/21
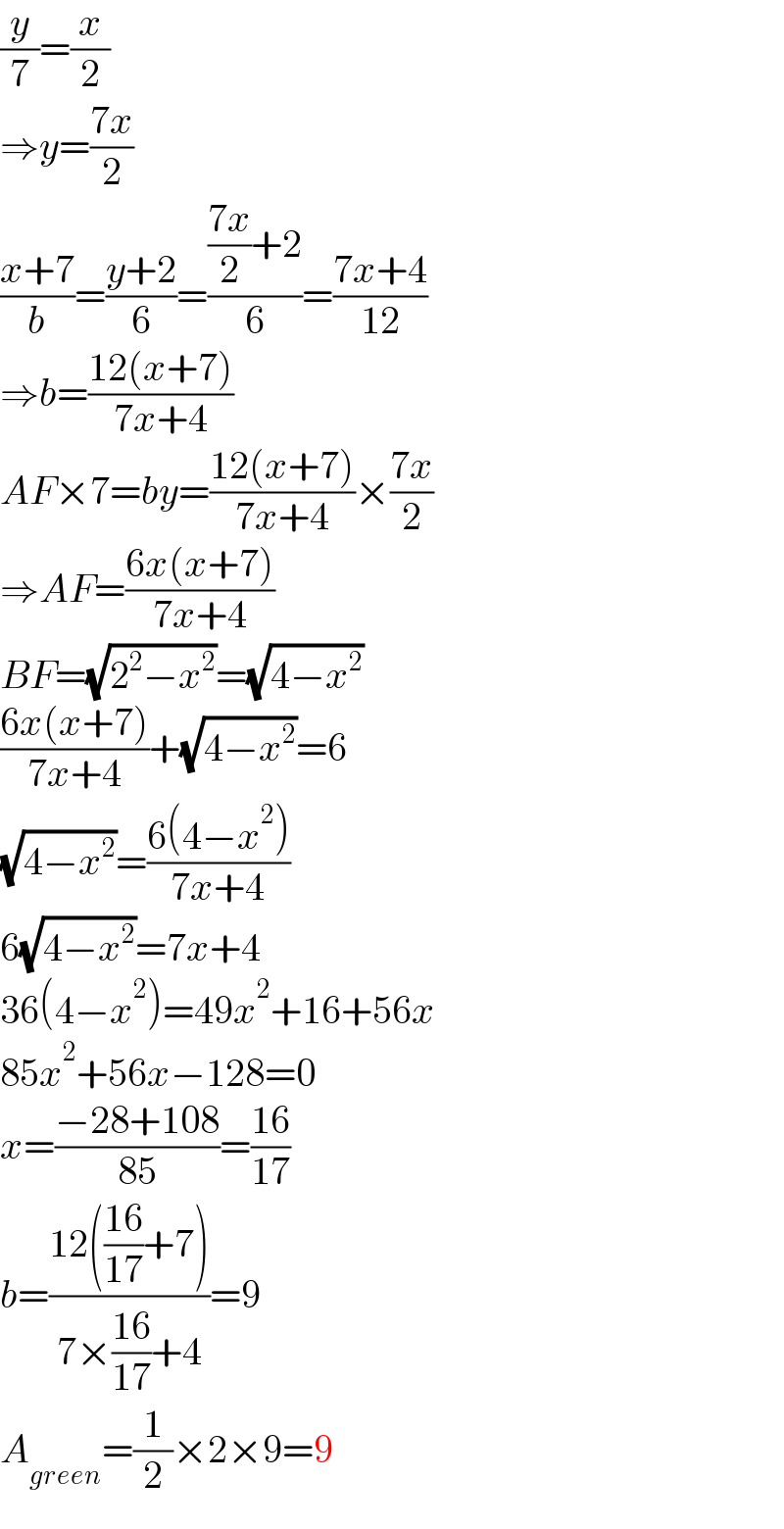
$$\frac{{y}}{\mathrm{7}}=\frac{{x}}{\mathrm{2}} \\ $$$$\Rightarrow{y}=\frac{\mathrm{7}{x}}{\mathrm{2}} \\ $$$$\frac{{x}+\mathrm{7}}{{b}}=\frac{{y}+\mathrm{2}}{\mathrm{6}}=\frac{\frac{\mathrm{7}{x}}{\mathrm{2}}+\mathrm{2}}{\mathrm{6}}=\frac{\mathrm{7}{x}+\mathrm{4}}{\mathrm{12}} \\ $$$$\Rightarrow{b}=\frac{\mathrm{12}\left({x}+\mathrm{7}\right)}{\mathrm{7}{x}+\mathrm{4}} \\ $$$${AF}×\mathrm{7}={by}=\frac{\mathrm{12}\left({x}+\mathrm{7}\right)}{\mathrm{7}{x}+\mathrm{4}}×\frac{\mathrm{7}{x}}{\mathrm{2}} \\ $$$$\Rightarrow{AF}=\frac{\mathrm{6}{x}\left({x}+\mathrm{7}\right)}{\mathrm{7}{x}+\mathrm{4}} \\ $$$${BF}=\sqrt{\mathrm{2}^{\mathrm{2}} −{x}^{\mathrm{2}} }=\sqrt{\mathrm{4}−{x}^{\mathrm{2}} } \\ $$$$\frac{\mathrm{6}{x}\left({x}+\mathrm{7}\right)}{\mathrm{7}{x}+\mathrm{4}}+\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }=\mathrm{6} \\ $$$$\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }=\frac{\mathrm{6}\left(\mathrm{4}−{x}^{\mathrm{2}} \right)}{\mathrm{7}{x}+\mathrm{4}} \\ $$$$\mathrm{6}\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }=\mathrm{7}{x}+\mathrm{4} \\ $$$$\mathrm{36}\left(\mathrm{4}−{x}^{\mathrm{2}} \right)=\mathrm{49}{x}^{\mathrm{2}} +\mathrm{16}+\mathrm{56}{x} \\ $$$$\mathrm{85}{x}^{\mathrm{2}} +\mathrm{56}{x}−\mathrm{128}=\mathrm{0} \\ $$$${x}=\frac{−\mathrm{28}+\mathrm{108}}{\mathrm{85}}=\frac{\mathrm{16}}{\mathrm{17}} \\ $$$${b}=\frac{\mathrm{12}\left(\frac{\mathrm{16}}{\mathrm{17}}+\mathrm{7}\right)}{\mathrm{7}×\frac{\mathrm{16}}{\mathrm{17}}+\mathrm{4}}=\mathrm{9} \\ $$$${A}_{{green}} =\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{2}×\mathrm{9}=\mathrm{9} \\ $$
Commented by Tawa11 last updated on 09/Dec/21

$$\mathrm{Great}\:\mathrm{sir}. \\ $$
