Question Number 160981 by mathlove last updated on 10/Dec/21

Commented by cortano last updated on 10/Dec/21
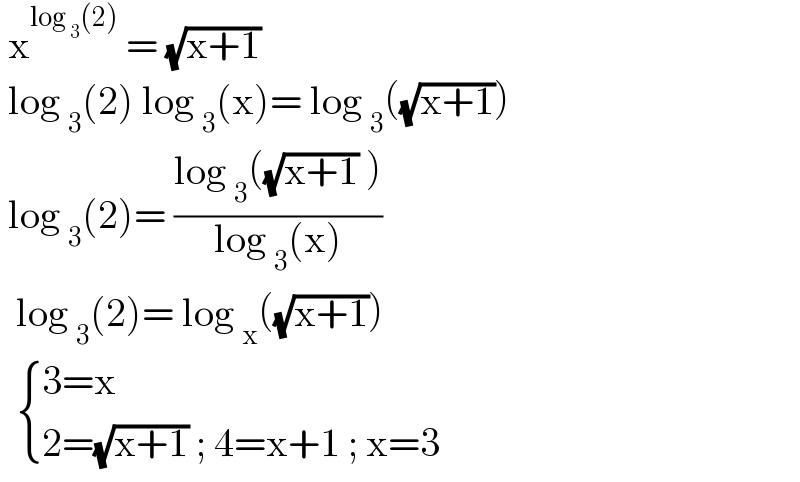
$$\:\mathrm{x}^{\mathrm{log}\:_{\mathrm{3}} \left(\mathrm{2}\right)} \:=\:\sqrt{\mathrm{x}+\mathrm{1}}\: \\ $$$$\:\mathrm{log}\:_{\mathrm{3}} \left(\mathrm{2}\right)\:\mathrm{log}\:_{\mathrm{3}} \left(\mathrm{x}\right)=\:\mathrm{log}\:_{\mathrm{3}} \left(\sqrt{\mathrm{x}+\mathrm{1}}\right) \\ $$$$\:\mathrm{log}\:_{\mathrm{3}} \left(\mathrm{2}\right)=\:\frac{\mathrm{log}\:_{\mathrm{3}} \left(\sqrt{\mathrm{x}+\mathrm{1}}\:\right)}{\mathrm{log}\:_{\mathrm{3}} \left(\mathrm{x}\right)} \\ $$$$\:\:\mathrm{log}\:_{\mathrm{3}} \left(\mathrm{2}\right)=\:\mathrm{log}\:_{\mathrm{x}} \left(\sqrt{\mathrm{x}+\mathrm{1}}\right) \\ $$$$\:\:\begin{cases}{\mathrm{3}=\mathrm{x}}\\{\mathrm{2}=\sqrt{\mathrm{x}+\mathrm{1}}\:;\:\mathrm{4}=\mathrm{x}+\mathrm{1}\:;\:\mathrm{x}=\mathrm{3}}\end{cases}\: \\ $$
