Menu Close

Question-160993

Tinku Tara 0 Comments
Pin




Question Number 160993 by gbanda95 last updated on 10/Dec/21
Answered by mathmax by abdo last updated on 10/Dec/21
∫_0 ^(π/2) x^3 sinx dx =I_3 =3((π/2))^2 −3(3−1)I_1 =((3π^2 )/4)−6I_1 I_1 =∫_0 ^(π/2) xsinx dx =[−xcosx]_0 ^(π/2) +∫_0 ^(π/2) cosxdx =[sinx]_0 ^(π/2) =1 ⇒∫_0 ^(π/2) x^3 sinx dx =((3π^2 )/4)−6
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{x}^{\mathrm{3}} \mathrm{sinx}\:\mathrm{dx}\:=\mathrm{I}_{\mathrm{3}} =\mathrm{3}\left(\frac{\pi}{\mathrm{2}}\right)^{\mathrm{2}} −\mathrm{3}\left(\mathrm{3}−\mathrm{1}\right)\mathrm{I}_{\mathrm{1}} =\frac{\mathrm{3}\pi^{\mathrm{2}} }{\mathrm{4}}−\mathrm{6I}_{\mathrm{1}} \\ $$$$\mathrm{I}_{\mathrm{1}} =\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{xsinx}\:\mathrm{dx}\:=\left[−\mathrm{xcosx}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} +\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{cosxdx} \\ $$$$=\left[\mathrm{sinx}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:=\mathrm{1}\:\Rightarrow\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{x}^{\mathrm{3}} \mathrm{sinx}\:\mathrm{dx}\:=\frac{\mathrm{3}\pi^{\mathrm{2}} }{\mathrm{4}}−\mathrm{6} \\ $$
Answered by mathmax by abdo last updated on 10/Dec/21
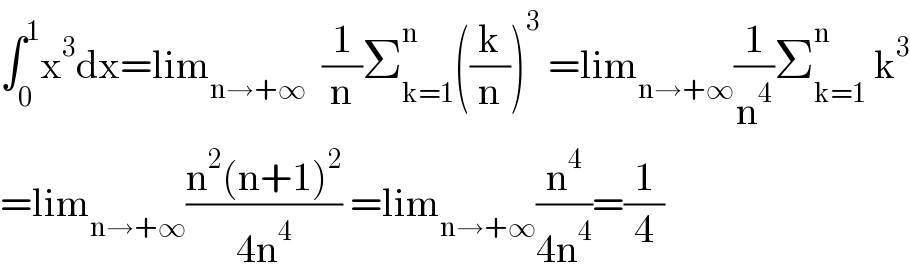
∫_0 ^1 x^3 dx=lim_(n→+∞) (1/n)Σ_(k=1) ^n ((k/n))^3 =lim_(n→+∞) (1/n^4 )Σ_(k=1) ^n k^3 =lim_(n→+∞) ((n^2 (n+1)^2 )/(4n^4 )) =lim_(n→+∞) (n^4 /(4n^4 ))=(1/4)
$$\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{x}^{\mathrm{3}} \mathrm{dx}=\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \:\:\frac{\mathrm{1}}{\mathrm{n}}\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \left(\frac{\mathrm{k}}{\mathrm{n}}\right)^{\mathrm{3}} \:=\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \frac{\mathrm{1}}{\mathrm{n}^{\mathrm{4}} }\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{k}^{\mathrm{3}} \\ $$$$=\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \frac{\mathrm{n}^{\mathrm{2}} \left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{4n}^{\mathrm{4}} }\:=\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \frac{\mathrm{n}^{\mathrm{4}} }{\mathrm{4n}^{\mathrm{4}} }=\frac{\mathrm{1}}{\mathrm{4}} \\ $$
Answered by mathmax by abdo last updated on 10/Dec/21
I_n =∫_0 ^(π/2) x^n sinx dx by parts u=x^n and v^′ =sinx I_n =[−x^n cosx]_0 ^(π/2) +∫_0 ^(π/2) nx^(n−1) cosx dx =n{ [x^(n−1) sinx]_0 ^(π/2) −∫_0 ^(π/2) (n−1)x^(n−2) sinx dx} =n((π/2))^(n−1) −n(n−1)I_(n−2) with n≥2
$$\mathrm{I}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{x}^{\mathrm{n}} \mathrm{sinx}\:\mathrm{dx}\:\:\mathrm{by}\:\mathrm{parts}\:\:\mathrm{u}=\mathrm{x}^{\mathrm{n}} \:\mathrm{and}\:\mathrm{v}^{'} \:=\mathrm{sinx} \\ $$$$\mathrm{I}_{\mathrm{n}} =\left[−\mathrm{x}^{\mathrm{n}} \mathrm{cosx}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:+\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\mathrm{nx}^{\mathrm{n}−\mathrm{1}} \mathrm{cosx}\:\mathrm{dx} \\ $$$$=\mathrm{n}\left\{\:\:\left[\mathrm{x}^{\mathrm{n}−\mathrm{1}} \mathrm{sinx}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} −\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\mathrm{n}−\mathrm{1}\right)\mathrm{x}^{\mathrm{n}−\mathrm{2}} \mathrm{sinx}\:\mathrm{dx}\right\} \\ $$$$=\mathrm{n}\left(\frac{\pi}{\mathrm{2}}\right)^{\mathrm{n}−\mathrm{1}} −\mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)\mathrm{I}_{\mathrm{n}−\mathrm{2}} \:\:\:\:\mathrm{with}\:\mathrm{n}\geqslant\mathrm{2} \\ $$
Answered by mathmax by abdo last updated on 10/Dec/21
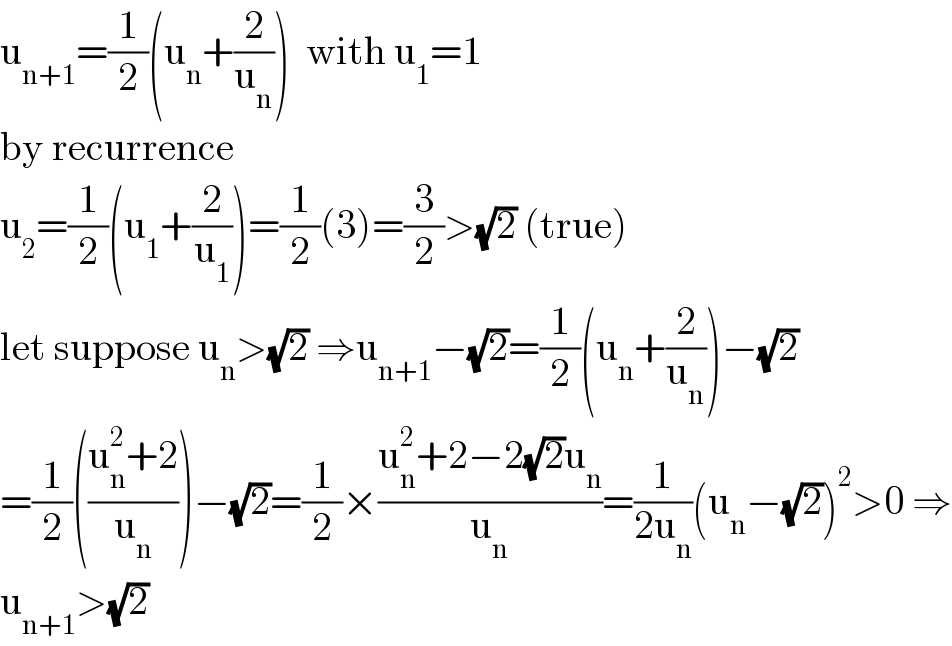
u_(n+1) =(1/2)(u_n +(2/u_n )) with u_1 =1 by recurrence u_2 =(1/2)(u_1 +(2/u_1 ))=(1/2)(3)=(3/2)>(√2) (true) let suppose u_n >(√2) ⇒u_(n+1) −(√2)=(1/2)(u_n +(2/u_n ))−(√2) =(1/2)(((u_n ^2 +2)/u_n ))−(√2)=(1/2)×((u_n ^2 +2−2(√2)u_n )/u_n )=(1/(2u_n ))(u_n −(√2))^2 >0 ⇒ u_(n+1) >(√2)
$$\mathrm{u}_{\mathrm{n}+\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{u}_{\mathrm{n}} +\frac{\mathrm{2}}{\mathrm{u}_{\mathrm{n}} }\right)\:\:\mathrm{with}\:\mathrm{u}_{\mathrm{1}} =\mathrm{1} \\ $$$$\mathrm{by}\:\mathrm{recurrence} \\ $$$$\mathrm{u}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{u}_{\mathrm{1}} +\frac{\mathrm{2}}{\mathrm{u}_{\mathrm{1}} }\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{3}\right)=\frac{\mathrm{3}}{\mathrm{2}}>\sqrt{\mathrm{2}}\:\left(\mathrm{true}\right) \\ $$$$\mathrm{let}\:\mathrm{suppose}\:\mathrm{u}_{\mathrm{n}} >\sqrt{\mathrm{2}}\:\Rightarrow\mathrm{u}_{\mathrm{n}+\mathrm{1}} −\sqrt{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{u}_{\mathrm{n}} +\frac{\mathrm{2}}{\mathrm{u}_{\mathrm{n}} }\right)−\sqrt{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{u}_{\mathrm{n}} ^{\mathrm{2}} +\mathrm{2}}{\mathrm{u}_{\mathrm{n}} }\right)−\sqrt{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{u}_{\mathrm{n}} ^{\mathrm{2}} +\mathrm{2}−\mathrm{2}\sqrt{\mathrm{2}}\mathrm{u}_{\mathrm{n}} }{\mathrm{u}_{\mathrm{n}} }=\frac{\mathrm{1}}{\mathrm{2u}_{\mathrm{n}} }\left(\mathrm{u}_{\mathrm{n}} −\sqrt{\mathrm{2}}\right)^{\mathrm{2}} >\mathrm{0}\:\Rightarrow \\ $$$$\mathrm{u}_{\mathrm{n}+\mathrm{1}} >\sqrt{\mathrm{2}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *