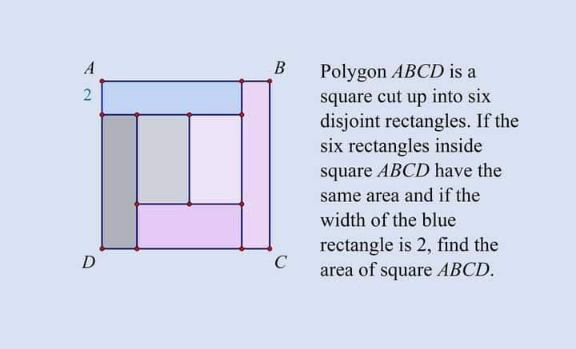
Question Number 161023 by cortano last updated on 10/Dec/21
Commented by som(math1967) last updated on 11/Dec/21

$$\mathrm{100}\:{squnits}\:? \\ $$
Commented by cortano last updated on 11/Dec/21

$${yes} \\ $$
Answered by som(math1967) last updated on 11/Dec/21
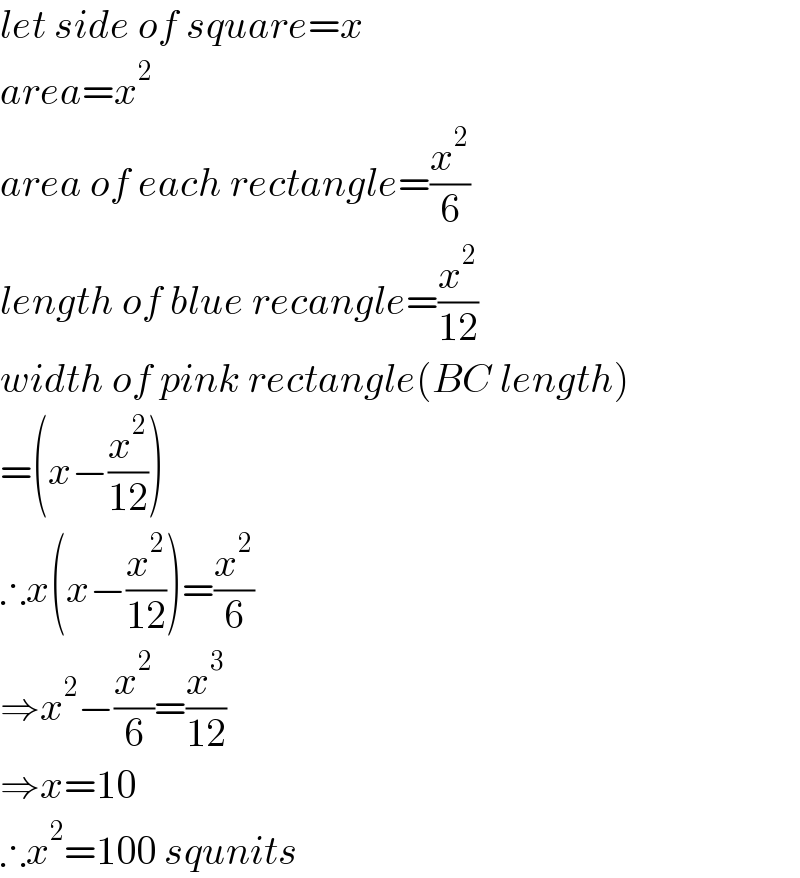
$${let}\:{side}\:{of}\:{square}={x} \\ $$$${area}={x}^{\mathrm{2}} \\ $$$${area}\:{of}\:{each}\:{rectangle}=\frac{{x}^{\mathrm{2}} }{\mathrm{6}} \\ $$$${length}\:{of}\:{blue}\:{recangle}=\frac{{x}^{\mathrm{2}} }{\mathrm{12}} \\ $$$${width}\:{of}\:{pink}\:{rectangle}\left({BC}\:{length}\right) \\ $$$$=\left({x}−\frac{{x}^{\mathrm{2}} }{\mathrm{12}}\right) \\ $$$$\therefore{x}\left({x}−\frac{{x}^{\mathrm{2}} }{\mathrm{12}}\right)=\frac{{x}^{\mathrm{2}} }{\mathrm{6}} \\ $$$$\Rightarrow{x}^{\mathrm{2}} −\frac{{x}^{\mathrm{2}} }{\mathrm{6}}=\frac{{x}^{\mathrm{3}} }{\mathrm{12}} \\ $$$$\Rightarrow{x}=\mathrm{10} \\ $$$$\therefore{x}^{\mathrm{2}} =\mathrm{100}\:{squnits} \\ $$
