Question Number 161102 by cortano last updated on 12/Dec/21

Commented by Abdulazizov last updated on 12/Dec/21

$$ \\ $$
Answered by mr W last updated on 13/Dec/21
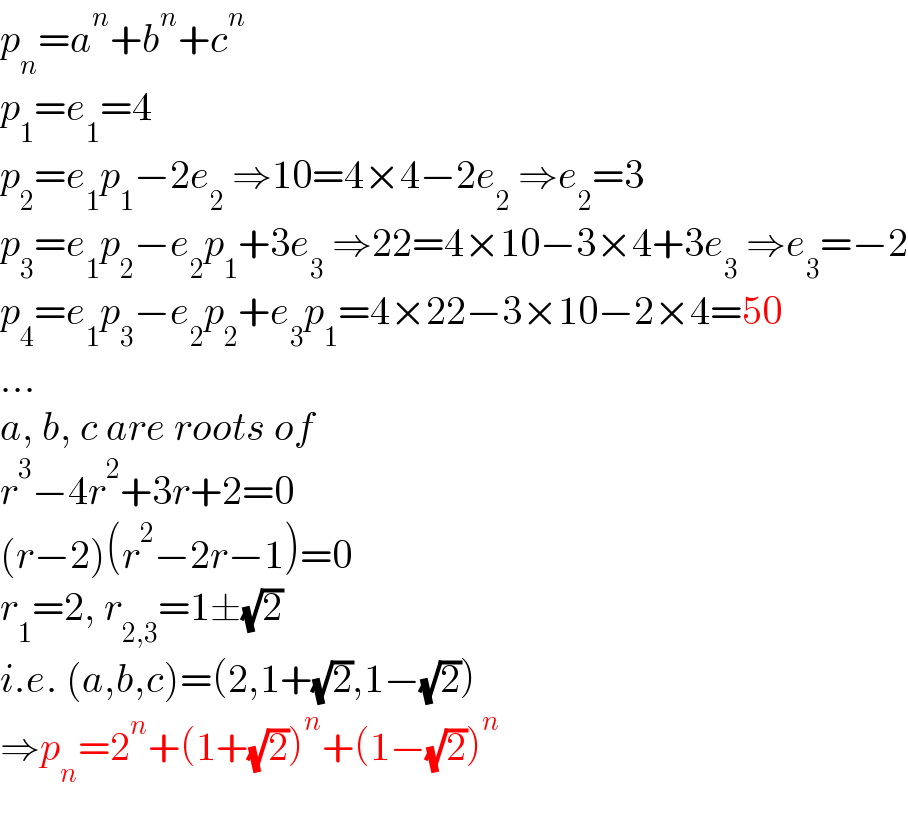
$${p}_{{n}} ={a}^{{n}} +{b}^{{n}} +{c}^{{n}} \\ $$$${p}_{\mathrm{1}} ={e}_{\mathrm{1}} =\mathrm{4} \\ $$$${p}_{\mathrm{2}} ={e}_{\mathrm{1}} {p}_{\mathrm{1}} −\mathrm{2}{e}_{\mathrm{2}} \:\Rightarrow\mathrm{10}=\mathrm{4}×\mathrm{4}−\mathrm{2}{e}_{\mathrm{2}} \:\Rightarrow{e}_{\mathrm{2}} =\mathrm{3} \\ $$$${p}_{\mathrm{3}} ={e}_{\mathrm{1}} {p}_{\mathrm{2}} −{e}_{\mathrm{2}} {p}_{\mathrm{1}} +\mathrm{3}{e}_{\mathrm{3}} \:\Rightarrow\mathrm{22}=\mathrm{4}×\mathrm{10}−\mathrm{3}×\mathrm{4}+\mathrm{3}{e}_{\mathrm{3}} \:\Rightarrow{e}_{\mathrm{3}} =−\mathrm{2} \\ $$$${p}_{\mathrm{4}} ={e}_{\mathrm{1}} {p}_{\mathrm{3}} −{e}_{\mathrm{2}} {p}_{\mathrm{2}} +{e}_{\mathrm{3}} {p}_{\mathrm{1}} =\mathrm{4}×\mathrm{22}−\mathrm{3}×\mathrm{10}−\mathrm{2}×\mathrm{4}=\mathrm{50} \\ $$$$… \\ $$$${a},\:{b},\:{c}\:{are}\:{roots}\:{of} \\ $$$${r}^{\mathrm{3}} −\mathrm{4}{r}^{\mathrm{2}} +\mathrm{3}{r}+\mathrm{2}=\mathrm{0} \\ $$$$\left({r}−\mathrm{2}\right)\left({r}^{\mathrm{2}} −\mathrm{2}{r}−\mathrm{1}\right)=\mathrm{0} \\ $$$${r}_{\mathrm{1}} =\mathrm{2},\:{r}_{\mathrm{2},\mathrm{3}} =\mathrm{1}\pm\sqrt{\mathrm{2}} \\ $$$${i}.{e}.\:\left({a},{b},{c}\right)=\left(\mathrm{2},\mathrm{1}+\sqrt{\mathrm{2}},\mathrm{1}−\sqrt{\mathrm{2}}\right) \\ $$$$\Rightarrow{p}_{{n}} =\mathrm{2}^{{n}} +\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{{n}} +\left(\mathrm{1}−\sqrt{\mathrm{2}}\right)^{{n}} \\ $$
Commented by Rasheed.Sindhi last updated on 14/Dec/21
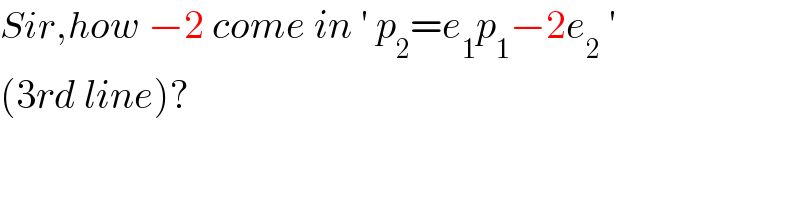
$${Sir},{how}\:−\mathrm{2}\:{come}\:{in}\:'\:{p}_{\mathrm{2}} ={e}_{\mathrm{1}} {p}_{\mathrm{1}} −\mathrm{2}{e}_{\mathrm{2}} \:'\: \\ $$$$\left(\mathrm{3}{rd}\:{line}\right)? \\ $$
Commented by mr W last updated on 14/Dec/21

$${generally} \\ $$$${p}_{{n}} ={e}_{\mathrm{1}} {p}_{{n}−\mathrm{1}} −{e}_{\mathrm{2}} {p}_{{n}−\mathrm{2}} +{e}_{\mathrm{3}} {p}_{{n}−\mathrm{3}} −…+\left(−\mathrm{1}\right)^{{n}} {e}_{{n}−\mathrm{1}} {p}_{\mathrm{1}} +\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} {ne}_{{n}} \\ $$$${see}\:{Newton}'{s}\:{identities}. \\ $$$$ \\ $$$${certainly}\:{we}\:{can}\:{also}\:{check}\:{it}: \\ $$$$\left({a}+{b}+{c}\right)^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +\mathrm{2}\left({ab}+{bc}+{ca}\right) \\ $$$${e}_{\mathrm{1}} {p}_{\mathrm{1}} ={p}_{\mathrm{2}} +\mathrm{2}{e}_{\mathrm{2}} \\ $$$$\Rightarrow{p}_{\mathrm{2}} ={e}_{\mathrm{1}} {p}_{\mathrm{1}} −\mathrm{2}{e}_{\mathrm{2}} \\ $$
Commented by Rasheed.Sindhi last updated on 14/Dec/21
$$\mathbb{T}\mathrm{han}\Bbbk\mathrm{s}\:\mathrm{a}\:\mathrm{lOt}\:\mathbb{S}\mathrm{ir}! \\ $$
