Question Number 161214 by kapoorshah last updated on 14/Dec/21
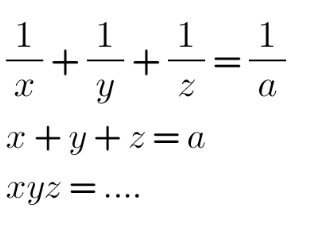
Commented by mr W last updated on 14/Dec/21
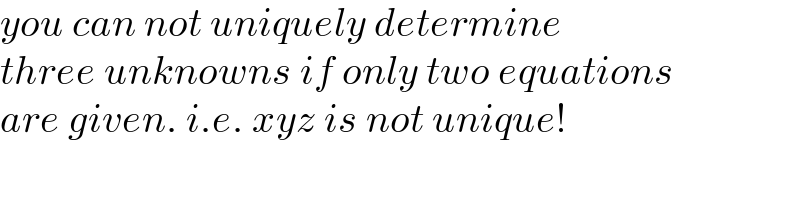
$${you}\:{can}\:{not}\:{uniquely}\:{determine} \\ $$$${three}\:{unknowns}\:{if}\:{only}\:{two}\:{equations} \\ $$$${are}\:{given}.\:{i}.{e}.\:{xyz}\:{is}\:{not}\:{unique}! \\ $$
Commented by mr W last updated on 14/Dec/21
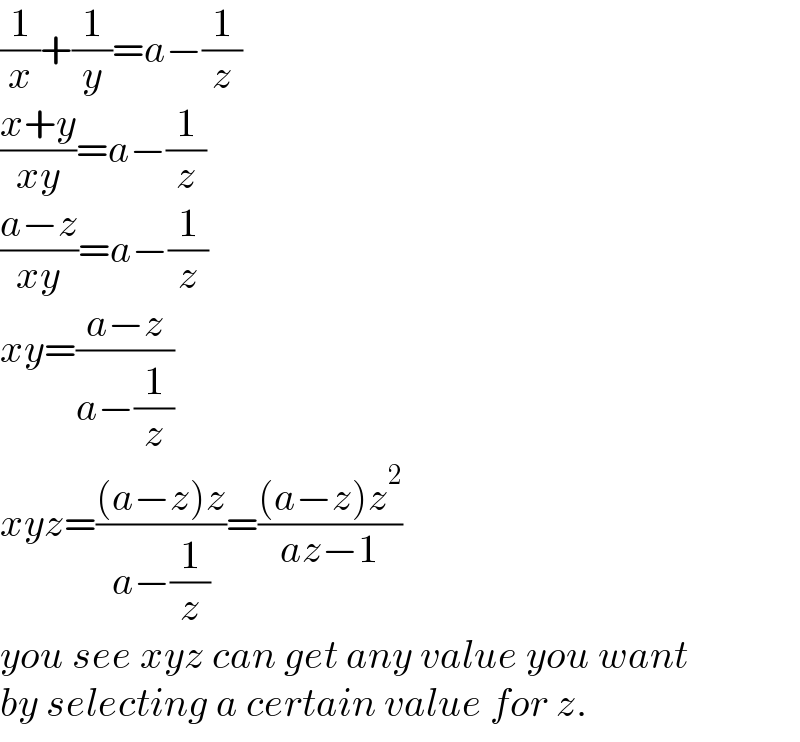
$$\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{y}}={a}−\frac{\mathrm{1}}{{z}} \\ $$$$\frac{{x}+{y}}{{xy}}={a}−\frac{\mathrm{1}}{{z}} \\ $$$$\frac{{a}−{z}}{{xy}}={a}−\frac{\mathrm{1}}{{z}} \\ $$$${xy}=\frac{{a}−{z}}{{a}−\frac{\mathrm{1}}{{z}}} \\ $$$${xyz}=\frac{\left({a}−{z}\right){z}}{{a}−\frac{\mathrm{1}}{{z}}}=\frac{\left({a}−{z}\right){z}^{\mathrm{2}} }{{az}−\mathrm{1}} \\ $$$${you}\:{see}\:{xyz}\:{can}\:{get}\:{any}\:{value}\:{you}\:{want} \\ $$$${by}\:{selecting}\:{a}\:{certain}\:{value}\:{for}\:{z}. \\ $$
Commented by kapoorshah last updated on 14/Dec/21
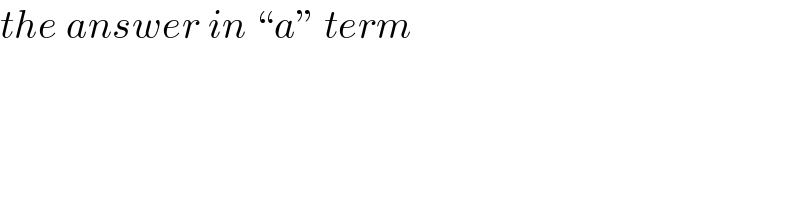
$${the}\:{answer}\:{in}\:“{a}''\:{term} \\ $$
Commented by mr W last updated on 14/Dec/21
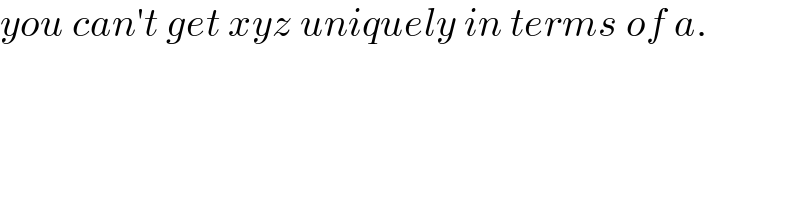
$${you}\:{can}'{t}\:{get}\:{xyz}\:{uniquely}\:{in}\:{terms}\:{of}\:{a}. \\ $$
Commented by kapoorshah last updated on 14/Dec/21
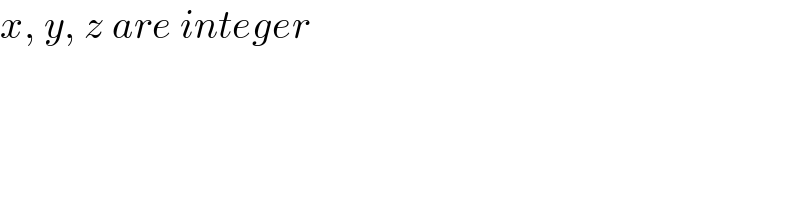
$${x},\:{y},\:{z}\:{are}\:{integer} \\ $$
Commented by mr W last updated on 14/Dec/21
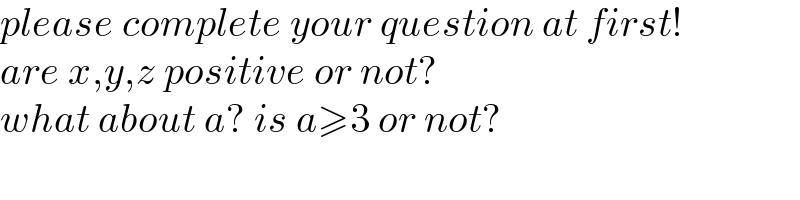
$${please}\:{complete}\:{your}\:{question}\:{at}\:{first}! \\ $$$${are}\:{x},{y},{z}\:{positive}\:{or}\:{not}? \\ $$$${what}\:{about}\:{a}?\:{is}\:{a}\geqslant\mathrm{3}\:{or}\:{not}? \\ $$
