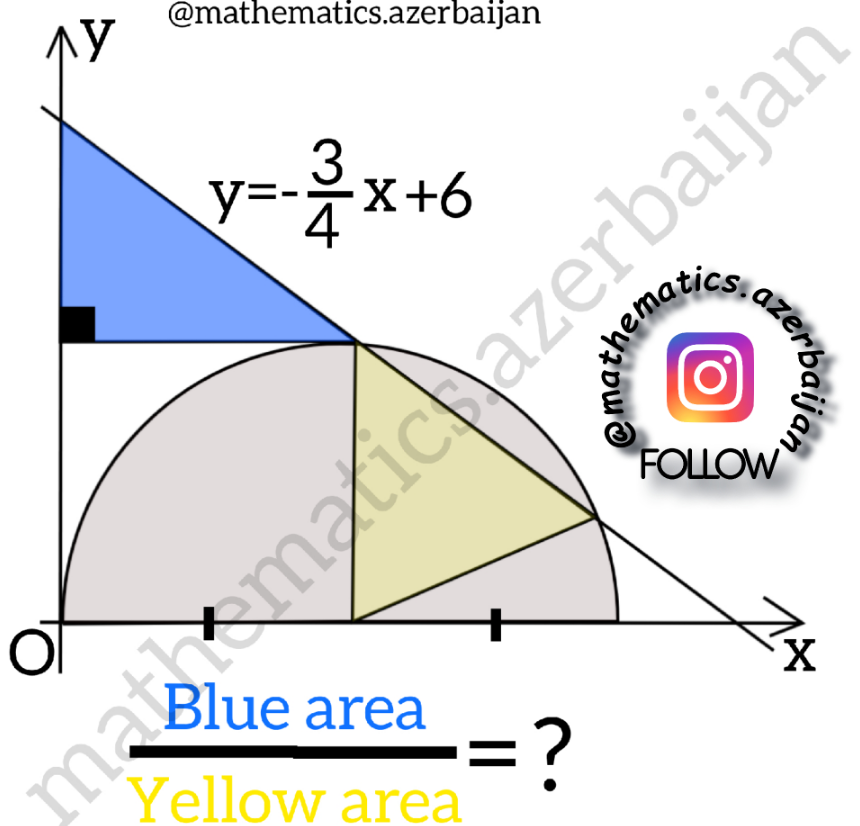
Question Number 161257 by amin96 last updated on 15/Dec/21
Commented by amin96 last updated on 15/Dec/21

$${yes}\:.\:{solution}? \\ $$
Answered by som(math1967) last updated on 15/Dec/21

$${let}\:\angle{ACE}=\angle{ABO}=\theta \\ $$$$\therefore\angle{FCL}=\mathrm{90}−\theta \\ $$$${radius}\:{of}\:{semicircle}={r} \\ $$$$\:{tan}\theta=\frac{\mathrm{6}}{\mathrm{8}}=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$${from}\:\bigtriangleup{AEC}\: \\ $$$$\:{AE}={rtan}\theta \\ $$$$\therefore{ar}\:\bigtriangleup{AEC}\:\left({blue}\right)=\frac{\mathrm{1}}{\mathrm{2}}×{r}×{rtan}\theta \\ $$$$=\frac{{r}^{\mathrm{2}} {tan}\theta}{\mathrm{2}} \\ $$$${from}\:\bigtriangleup{CFD} \\ $$$$\:{FL}={rsin}\left(\mathrm{90}−\theta\right)={rcos}\theta \\ $$$${CL}={rcos}\left(\mathrm{90}−\theta\right)={rsin}\theta \\ $$$${ar}\:\bigtriangleup{CFD}\left({Yellow}\right)={r}^{\mathrm{2}} {sin}\theta{cos}\theta \\ $$$$\:\therefore\frac{\boldsymbol{{BLUE}}}{\boldsymbol{{YELLOW}}}=\frac{\boldsymbol{{r}}^{\mathrm{2}} \boldsymbol{{tan}\theta}}{\mathrm{2}\boldsymbol{{r}}^{\mathrm{2}} \boldsymbol{{sin}\theta{cos}\theta}}=\frac{\boldsymbol{{sec}}^{\mathrm{2}} \boldsymbol{\theta}}{\mathrm{2}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{25}}{\mathrm{16}}=\frac{\mathrm{25}}{\mathrm{32}} \\ $$$$ \\ $$
Commented by som(math1967) last updated on 15/Dec/21

Commented by Tawa11 last updated on 15/Dec/21

$$\mathrm{Great}\:\mathrm{sir} \\ $$
Answered by Rasheed.Sindhi last updated on 15/Dec/21
Commented by Rasheed.Sindhi last updated on 15/Dec/21
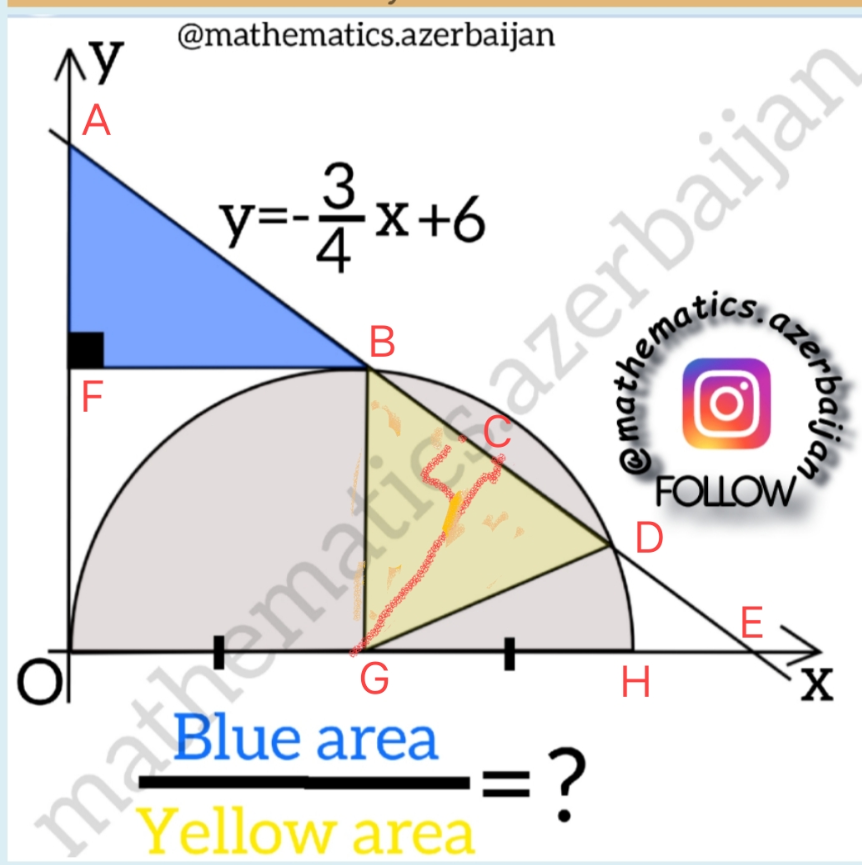
![Without Referencing Any Angle •A & E are y & x intercepts of y=−(3/4)x+6 A=(0,−(3/4)∙0+6)=(0,6) OA=6 B=(x,0)=(8,0) [∵ 0=−(3/4)x+6⇒x=8] OE=8 AE=(√(OA^2 +OE^2 ))=(√(6^2 +8^2 )) =10 •B=(r,r): y=−(3/4)x+6⇒r=−(3/4)r+6 ⇒r=((24)/7) •▲AFB: ⇒r=((24)/7)⇒BF=((24)/7) AF=6−r=6−((24)/7)=((18)/7) ▲AFB=(1/2)∙BF∙AF=(1/2)∙((24)/7)∙((18)/7)=((216)/(49)) •△AOE∼△GCB ((AE)/(BG))=((OA)/(BC))⇒((10)/( ((24)/7) ))=(6/(BC))⇒BC=((((24)/7)∙6)/(10)) =((24)/7)∙6∙(1/(10))=((72)/(35))⇒BC=((72)/(35)) GC=(√(BG^2 −BC^2 )) =(√((((24)/7))^2 −(((72)/(35)))^2 )) =((96)/(35)) • ▲BGC=(1/2)∙BC∙GC=(1/2)∙((72)/(35))∙((96)/(35)) ▲BGD=2∙▲BGC=((72∙96)/(35^2 )) • ((Blue)/(Yellow))=((▲AFB)/(▲BGD))=(((216)/(49))/((72∙96)/(35^2 )))=((216)/(49))∙((35^2 )/(72∙96)) =((25)/(32))](https://www.tinkutara.com/question/Q161278.png)
$$\mathbb{W}\mathrm{ithout}\:\mathbb{R}\mathrm{eferencing}\:\mathbb{A}\mathrm{ny}\:\mathbb{A}\mathrm{ngle} \\ $$$$\bullet\mathrm{A}\:\&\:\mathrm{E}\:\mathrm{are}\:\mathrm{y}\:\&\:\mathrm{x}\:\mathrm{intercepts}\:\:\mathrm{of}\:\mathrm{y}=−\frac{\mathrm{3}}{\mathrm{4}}\mathrm{x}+\mathrm{6} \\ $$$$\mathrm{A}=\left(\mathrm{0},−\frac{\mathrm{3}}{\mathrm{4}}\centerdot\mathrm{0}+\mathrm{6}\right)=\left(\mathrm{0},\mathrm{6}\right) \\ $$$$\mathrm{OA}=\mathrm{6} \\ $$$$\mathrm{B}=\left(\mathrm{x},\mathrm{0}\right)=\left(\mathrm{8},\mathrm{0}\right)\:\left[\because\:\mathrm{0}=−\frac{\mathrm{3}}{\mathrm{4}}\mathrm{x}+\mathrm{6}\Rightarrow\mathrm{x}=\mathrm{8}\right] \\ $$$$\mathrm{OE}=\mathrm{8} \\ $$$$\mathrm{AE}=\sqrt{\mathrm{OA}^{\mathrm{2}} +\mathrm{OE}^{\mathrm{2}} }=\sqrt{\mathrm{6}^{\mathrm{2}} +\mathrm{8}^{\mathrm{2}} }\:=\mathrm{10} \\ $$$$\bullet\mathrm{B}=\left(\mathrm{r},\mathrm{r}\right):\:\mathrm{y}=−\frac{\mathrm{3}}{\mathrm{4}}\mathrm{x}+\mathrm{6}\Rightarrow\mathrm{r}=−\frac{\mathrm{3}}{\mathrm{4}}\mathrm{r}+\mathrm{6} \\ $$$$\Rightarrow\mathrm{r}=\frac{\mathrm{24}}{\mathrm{7}} \\ $$$$\bullet\blacktriangle\mathrm{AFB}: \\ $$$$\:\:\:\Rightarrow\mathrm{r}=\frac{\mathrm{24}}{\mathrm{7}}\Rightarrow\mathrm{BF}=\frac{\mathrm{24}}{\mathrm{7}} \\ $$$$\:\:\:\mathrm{AF}=\mathrm{6}−\mathrm{r}=\mathrm{6}−\frac{\mathrm{24}}{\mathrm{7}}=\frac{\mathrm{18}}{\mathrm{7}} \\ $$$$\:\blacktriangle\mathrm{AFB}=\frac{\mathrm{1}}{\mathrm{2}}\centerdot\mathrm{BF}\centerdot\mathrm{AF}=\frac{\mathrm{1}}{\mathrm{2}}\centerdot\frac{\mathrm{24}}{\mathrm{7}}\centerdot\frac{\mathrm{18}}{\mathrm{7}}=\frac{\mathrm{216}}{\mathrm{49}} \\ $$$$\bullet\bigtriangleup\mathrm{AOE}\sim\bigtriangleup\mathrm{GCB} \\ $$$$\:\:\frac{\mathrm{AE}}{\mathrm{BG}}=\frac{\mathrm{OA}}{\mathrm{BC}}\Rightarrow\frac{\mathrm{10}}{\:\frac{\mathrm{24}}{\mathrm{7}}\:}=\frac{\mathrm{6}}{\mathrm{BC}}\Rightarrow\mathrm{BC}=\frac{\frac{\mathrm{24}}{\mathrm{7}}\centerdot\mathrm{6}}{\mathrm{10}} \\ $$$$\:\:=\frac{\mathrm{24}}{\mathrm{7}}\centerdot\mathrm{6}\centerdot\frac{\mathrm{1}}{\mathrm{10}}=\frac{\mathrm{72}}{\mathrm{35}}\Rightarrow\mathrm{BC}=\frac{\mathrm{72}}{\mathrm{35}} \\ $$$$\:\:\mathrm{GC}=\sqrt{\mathrm{BG}^{\mathrm{2}} −\mathrm{BC}^{\mathrm{2}} }\:=\sqrt{\left(\frac{\mathrm{24}}{\mathrm{7}}\right)^{\mathrm{2}} −\left(\frac{\mathrm{72}}{\mathrm{35}}\right)^{\mathrm{2}} }\: \\ $$$$\:\:\:=\frac{\mathrm{96}}{\mathrm{35}} \\ $$$$\bullet\:\blacktriangle\mathrm{BGC}=\frac{\mathrm{1}}{\mathrm{2}}\centerdot\mathrm{BC}\centerdot\mathrm{GC}=\frac{\mathrm{1}}{\mathrm{2}}\centerdot\frac{\mathrm{72}}{\mathrm{35}}\centerdot\frac{\mathrm{96}}{\mathrm{35}} \\ $$$$\:\:\blacktriangle\mathrm{BGD}=\mathrm{2}\centerdot\blacktriangle\mathrm{BGC}=\frac{\mathrm{72}\centerdot\mathrm{96}}{\mathrm{35}^{\mathrm{2}} } \\ $$$$\bullet\:\frac{{Blue}}{{Yellow}}=\frac{\blacktriangle\mathrm{AFB}}{\blacktriangle\mathrm{BGD}}=\frac{\frac{\mathrm{216}}{\mathrm{49}}}{\frac{\mathrm{72}\centerdot\mathrm{96}}{\mathrm{35}^{\mathrm{2}} }}=\frac{\mathrm{216}}{\mathrm{49}}\centerdot\frac{\mathrm{35}^{\mathrm{2}} }{\mathrm{72}\centerdot\mathrm{96}} \\ $$$$\:\:\:\:\:\:\:=\frac{\mathrm{25}}{\mathrm{32}} \\ $$
