Menu Close

Question-161322

Tinku Tara 0 Comments
Pin




Question Number 161322 by kapoorshah last updated on 16/Dec/21
Commented by cortano last updated on 16/Dec/21
sin (30°+10°+α)=b (1/2)cos (10°+α)+(1/2)(√3) sin (10°+α)=b cos (10°+α)+(√3) sin (10°+α)=2b (√3) (√(1−cos^2 t)) = 2b−cos t ; t=10°+α 3−3cos^2 t =4b^2 −4bcos t+cos^2 t 4cos^2 t−4b cos t+4b^2 −3 cos t = ((4b ± (√(16b^2 −16(4b^2 −3))))/8) cos t=((b±(√(3−3b^2 )))/2)
$$\mathrm{sin}\:\left(\mathrm{30}°+\mathrm{10}°+\alpha\right)={b} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:\left(\mathrm{10}°+\alpha\right)+\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{3}}\:\mathrm{sin}\:\left(\mathrm{10}°+\alpha\right)={b} \\ $$$$\mathrm{cos}\:\left(\mathrm{10}°+\alpha\right)+\sqrt{\mathrm{3}}\:\mathrm{sin}\:\left(\mathrm{10}°+\alpha\right)=\mathrm{2}{b} \\ $$$$\sqrt{\mathrm{3}}\:\sqrt{\mathrm{1}−\mathrm{cos}\:^{\mathrm{2}} {t}}\:=\:\mathrm{2}{b}−\mathrm{cos}\:{t}\:;\:{t}=\mathrm{10}°+\alpha \\ $$$$\mathrm{3}−\mathrm{3cos}\:^{\mathrm{2}} {t}\:=\mathrm{4}{b}^{\mathrm{2}} −\mathrm{4}{b}\mathrm{cos}\:{t}+\mathrm{cos}\:^{\mathrm{2}} {t} \\ $$$$\mathrm{4cos}\:^{\mathrm{2}} {t}−\mathrm{4}{b}\:\mathrm{cos}\:{t}+\mathrm{4}{b}^{\mathrm{2}} −\mathrm{3} \\ $$$$\mathrm{cos}\:{t}\:=\:\frac{\mathrm{4}{b}\:\pm\:\sqrt{\mathrm{16}{b}^{\mathrm{2}} −\mathrm{16}\left(\mathrm{4}{b}^{\mathrm{2}} −\mathrm{3}\right)}}{\mathrm{8}} \\ $$$$\mathrm{cos}\:{t}=\frac{{b}\pm\sqrt{\mathrm{3}−\mathrm{3}{b}^{\mathrm{2}} }}{\mathrm{2}} \\ $$
Commented by MJS_new last updated on 16/Dec/21
the calculation is right but for any given angle α the answer is ((b−(√(3−3b^2 )))/2) xor ((b+(√(3−3b^2 )))/2) and thus you must clearify your answer
$$\mathrm{the}\:\mathrm{calculation}\:\mathrm{is}\:\mathrm{right}\:\mathrm{but}\:\mathrm{for}\:\mathrm{any}\:\mathrm{given} \\ $$$$\mathrm{angle}\:\alpha\:\mathrm{the}\:\mathrm{answer}\:\mathrm{is}\:\frac{{b}−\sqrt{\mathrm{3}−\mathrm{3}{b}^{\mathrm{2}} }}{\mathrm{2}}\:\mathrm{xor}\:\frac{{b}+\sqrt{\mathrm{3}−\mathrm{3}{b}^{\mathrm{2}} }}{\mathrm{2}} \\ $$$$\mathrm{and}\:\mathrm{thus}\:\mathrm{you}\:\mathrm{must}\:\mathrm{clearify}\:\mathrm{your}\:\mathrm{answer} \\ $$
Commented by cortano last updated on 16/Dec/21
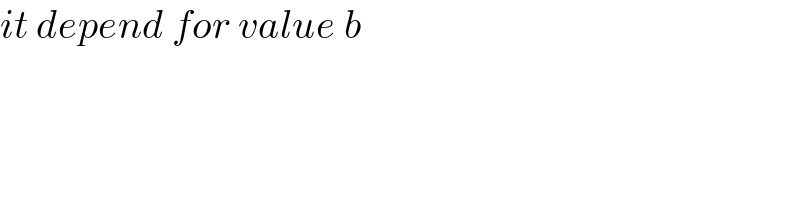
it depend for value b
$${it}\:{depend}\:{for}\:{value}\:{b} \\ $$
Commented by MJS_new last updated on 17/Dec/21
this is what I think was missing let 0°≤α<360° 0≤α<50°∨230°≤α<360° ⇒ cos (α+10°) =((b+(√(3(1−b^2 ))))/2) 50°≤α<230° ⇒ cos (α+10°) =((b−(√(3(1−b^2 ))))/2)
$$\mathrm{this}\:\mathrm{is}\:\mathrm{what}\:\mathrm{I}\:\mathrm{think}\:\mathrm{was}\:\mathrm{missing} \\ $$$$\mathrm{let}\:\mathrm{0}°\leqslant\alpha<\mathrm{360}° \\ $$$$\mathrm{0}\leqslant\alpha<\mathrm{50}°\vee\mathrm{230}°\leqslant\alpha<\mathrm{360}°\:\Rightarrow\:\mathrm{cos}\:\left(\alpha+\mathrm{10}°\right)\:=\frac{{b}+\sqrt{\mathrm{3}\left(\mathrm{1}−{b}^{\mathrm{2}} \right)}}{\mathrm{2}} \\ $$$$\mathrm{50}°\leqslant\alpha<\mathrm{230}°\:\Rightarrow\:\:\mathrm{cos}\:\left(\alpha+\mathrm{10}°\right)\:=\frac{{b}−\sqrt{\mathrm{3}\left(\mathrm{1}−{b}^{\mathrm{2}} \right)}}{\mathrm{2}} \\ $$
Answered by 1549442205PVT last updated on 16/Dec/21
sin(40^0 +α)=sin[30^0 +(10^0 +α)] =sin30^0 cos(10^0 +α)+cos30^0 sin(10^0 +α) =(1/2)cos(10^0 +α)+((√3)/2)sin(10^0 +α)=b we have the system of equations: { ((x+(√3)y=2b)),((x^2 +y^2 =1)) :}with x=cos(10^0 +α),y=sin(10^0 +α) ⇒(2b−(√3)y)^2 +y^2 =1⇔4y^2 −4b(√3)y+4b^2 −1=0 △′=12b^2 −16b^2 +4=4−4b^2 .Hence y=((2b(√3)±2(√(1−b^2 )))/4).From that x=cos(10^0 +α)=b−(√3)y=2b−((6b±2(√(3−3b^2 )))/4) =((2b±2(√(3−3b^2 )))/4)=((b±(√(3−3b^2 )))/2)
$${sin}\left(\mathrm{40}^{\mathrm{0}} +\alpha\right)={sin}\left[\mathrm{30}^{\mathrm{0}} +\left(\mathrm{10}^{\mathrm{0}} +\alpha\right)\right] \\ $$$$={sin}\mathrm{30}^{\mathrm{0}} {cos}\left(\mathrm{10}^{\mathrm{0}} +\alpha\right)+{cos}\mathrm{30}^{\mathrm{0}} {sin}\left(\mathrm{10}^{\mathrm{0}} +\alpha\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{cos}\left(\mathrm{10}^{\mathrm{0}} +\alpha\right)+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{sin}\left(\mathrm{10}^{\mathrm{0}} +\alpha\right)={b} \\ $$$${we}\:{have}\:{the}\:{system}\:{of}\:{equations}: \\ $$$$\begin{cases}{{x}+\sqrt{\mathrm{3}}{y}=\mathrm{2}{b}}\\{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{1}}\end{cases}{with}\:{x}={cos}\left(\mathrm{10}^{\mathrm{0}} +\alpha\right),{y}={sin}\left(\mathrm{10}^{\mathrm{0}} +\alpha\right) \\ $$$$\Rightarrow\left(\mathrm{2}{b}−\sqrt{\mathrm{3}}{y}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{1}\Leftrightarrow\mathrm{4}{y}^{\mathrm{2}} −\mathrm{4}{b}\sqrt{\mathrm{3}}{y}+\mathrm{4}{b}^{\mathrm{2}} −\mathrm{1}=\mathrm{0} \\ $$$$\bigtriangleup'=\mathrm{12}{b}^{\mathrm{2}} −\mathrm{16}{b}^{\mathrm{2}} +\mathrm{4}=\mathrm{4}−\mathrm{4}{b}^{\mathrm{2}} .{Hence} \\ $$$${y}=\frac{\mathrm{2}{b}\sqrt{\mathrm{3}}\pm\mathrm{2}\sqrt{\mathrm{1}−{b}^{\mathrm{2}} }}{\mathrm{4}}.{From}\:{that} \\ $$$${x}={cos}\left(\mathrm{10}^{\mathrm{0}} +\alpha\right)={b}−\sqrt{\mathrm{3}}{y}=\mathrm{2}{b}−\frac{\mathrm{6}{b}\pm\mathrm{2}\sqrt{\mathrm{3}−\mathrm{3}{b}^{\mathrm{2}} }}{\mathrm{4}} \\ $$$$=\frac{\mathrm{2}{b}\pm\mathrm{2}\sqrt{\mathrm{3}−\mathrm{3}{b}^{\mathrm{2}} }}{\mathrm{4}}=\frac{{b}\pm\sqrt{\mathrm{3}−\mathrm{3}{b}^{\mathrm{2}} }}{\mathrm{2}} \\ $$
Commented by 1549442205PVT last updated on 16/Dec/21
Thank you Sir,for sin (40^0 +α) exist b must satisfy ∣b∣≤1
$${Thank}\:{you}\:{Sir},{for}\:{sin}\:\left(\mathrm{40}^{\mathrm{0}} +\alpha\right)\:{exist} \\ $$$${b}\:{must}\:{satisfy}\:\mid{b}\mid\leqslant\mathrm{1} \\ $$
Commented by MJS_new last updated on 16/Dec/21
also here, read my comment above
$$\mathrm{also}\:\mathrm{here},\:\mathrm{read}\:\mathrm{my}\:\mathrm{comment}\:\mathrm{above} \\ $$
Commented by mr W last updated on 16/Dec/21
you didn′t understand MJS sir. say α=3°, sin (40°+3°)=sin 43°=b cos (10°+3°)=cos 13° which can only have one particular value, not two! as you give with ((b±(√(3−3b^2 )))/2). i.e. only + or −, not ±.
$${you}\:{didn}'{t}\:{understand}\:{MJS}\:{sir}. \\ $$$${say}\:\alpha=\mathrm{3}°,\:\mathrm{sin}\:\left(\mathrm{40}°+\mathrm{3}°\right)=\mathrm{sin}\:\mathrm{43}°={b} \\ $$$$\mathrm{cos}\:\left(\mathrm{10}°+\mathrm{3}°\right)=\mathrm{cos}\:\mathrm{13}°\:{which}\:{can}\:{only} \\ $$$${have}\:{one}\:{particular}\:{value},\:{not}\:{two}! \\ $$$${as}\:{you}\:{give}\:{with}\:\frac{{b}\pm\sqrt{\mathrm{3}−\mathrm{3}{b}^{\mathrm{2}} }}{\mathrm{2}}.\:{i}.{e}. \\ $$$${only}\:+\:{or}\:−,\:{not}\:\pm. \\ $$
Commented by cortano last updated on 17/Dec/21
how if α = 160° ? cos (α+160°)= cos 170° <0
$${how}\:{if}\:\alpha\:=\:\mathrm{160}°\:?\: \\ $$$$\:\mathrm{cos}\:\left(\alpha+\mathrm{160}°\right)=\:\mathrm{cos}\:\mathrm{170}°\:<\mathrm{0}\: \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *