Question Number 161338 by akolade last updated on 16/Dec/21
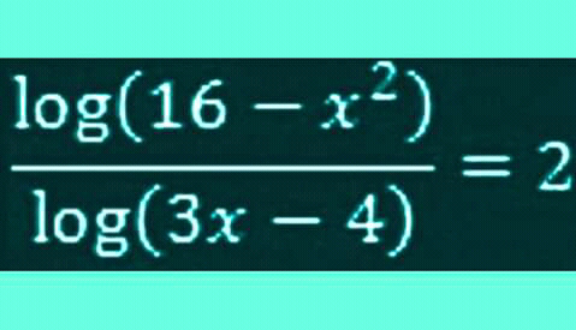
Commented by cortano last updated on 16/Dec/21
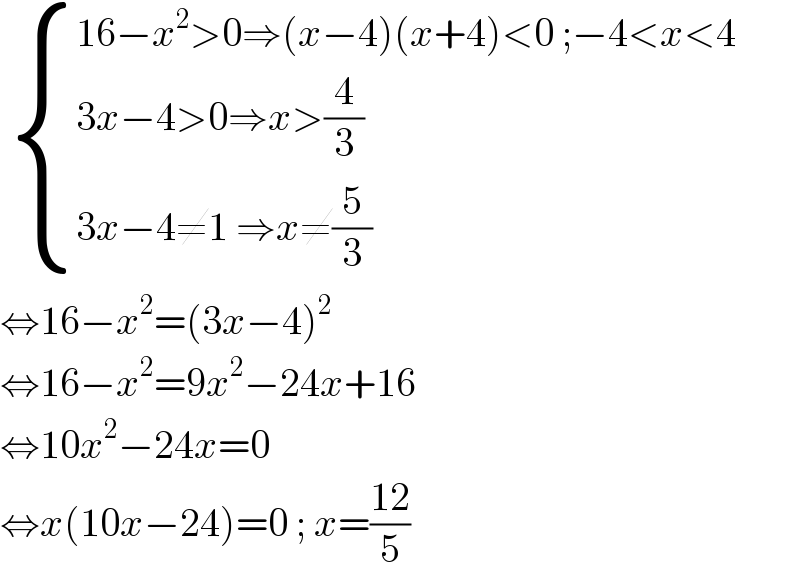
$$\:\begin{cases}{\mathrm{16}−{x}^{\mathrm{2}} >\mathrm{0}\Rightarrow\left({x}−\mathrm{4}\right)\left({x}+\mathrm{4}\right)<\mathrm{0}\:;−\mathrm{4}<{x}<\mathrm{4}}\\{\mathrm{3}{x}−\mathrm{4}>\mathrm{0}\Rightarrow{x}>\frac{\mathrm{4}}{\mathrm{3}}}\\{\mathrm{3}{x}−\mathrm{4}\neq\mathrm{1}\:\Rightarrow{x}\neq\frac{\mathrm{5}}{\mathrm{3}}}\end{cases} \\ $$$$\Leftrightarrow\mathrm{16}−{x}^{\mathrm{2}} =\left(\mathrm{3}{x}−\mathrm{4}\right)^{\mathrm{2}} \\ $$$$\Leftrightarrow\mathrm{16}−{x}^{\mathrm{2}} =\mathrm{9}{x}^{\mathrm{2}} −\mathrm{24}{x}+\mathrm{16} \\ $$$$\Leftrightarrow\mathrm{10}{x}^{\mathrm{2}} −\mathrm{24}{x}=\mathrm{0} \\ $$$$\Leftrightarrow{x}\left(\mathrm{10}{x}−\mathrm{24}\right)=\mathrm{0}\:;\:{x}=\frac{\mathrm{12}}{\mathrm{5}} \\ $$
Answered by kapoorshah last updated on 16/Dec/21
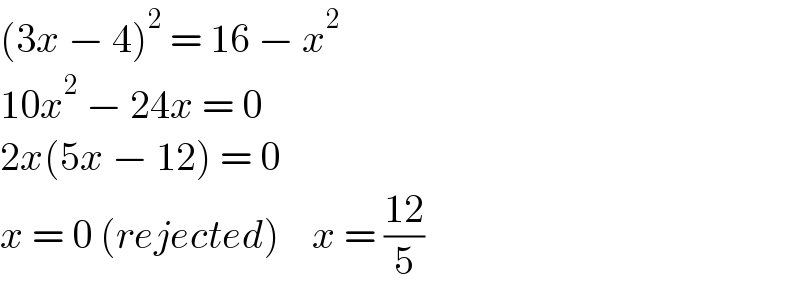
$$\left(\mathrm{3}{x}\:−\:\mathrm{4}\right)^{\mathrm{2}} \:=\:\mathrm{16}\:−\:{x}^{\mathrm{2}} \\ $$$$\mathrm{10}{x}^{\mathrm{2}} \:−\:\mathrm{24}{x}\:=\:\mathrm{0} \\ $$$$\mathrm{2}{x}\left(\mathrm{5}{x}\:−\:\mathrm{12}\right)\:=\:\mathrm{0} \\ $$$${x}\:=\:\mathrm{0}\:\left({rejected}\right)\:\:\:\:{x}\:=\:\frac{\mathrm{12}}{\mathrm{5}} \\ $$
