Question Number 161410 by saly last updated on 17/Dec/21
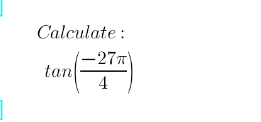
Commented by saly last updated on 17/Dec/21

$$\:\:{Thank}\:{you} \\ $$
Commented by saly last updated on 17/Dec/21

$$\:\:{Do}\:{you}\:{help}\:{me} \\ $$
Commented by geron last updated on 17/Dec/21
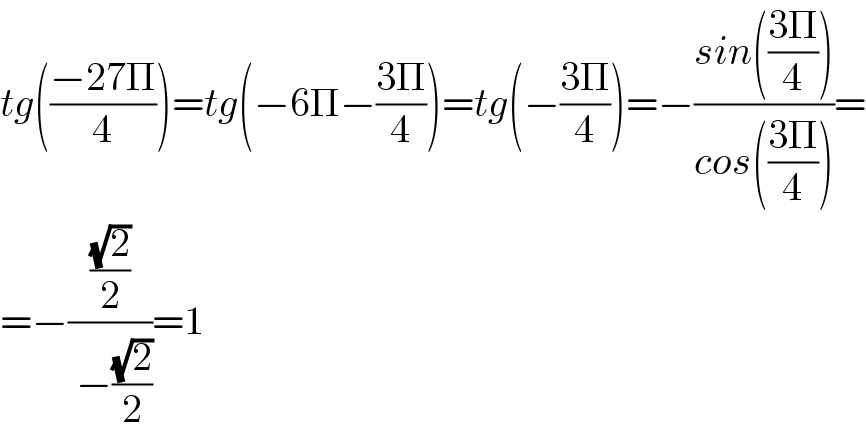
$${tg}\left(\frac{−\mathrm{27}\Pi}{\mathrm{4}}\right)={tg}\left(−\mathrm{6}\Pi−\frac{\mathrm{3}\Pi}{\mathrm{4}}\right)={tg}\left(−\frac{\mathrm{3}\Pi}{\mathrm{4}}\right)=−\frac{{sin}\left(\frac{\mathrm{3}\Pi}{\mathrm{4}}\right)}{{cos}\left(\frac{\mathrm{3}\Pi}{\mathrm{4}}\right)}= \\ $$$$=−\frac{\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}}{\:−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}}=\mathrm{1} \\ $$
