Question Number 161424 by cherokeesay last updated on 17/Dec/21
Answered by aleks041103 last updated on 17/Dec/21
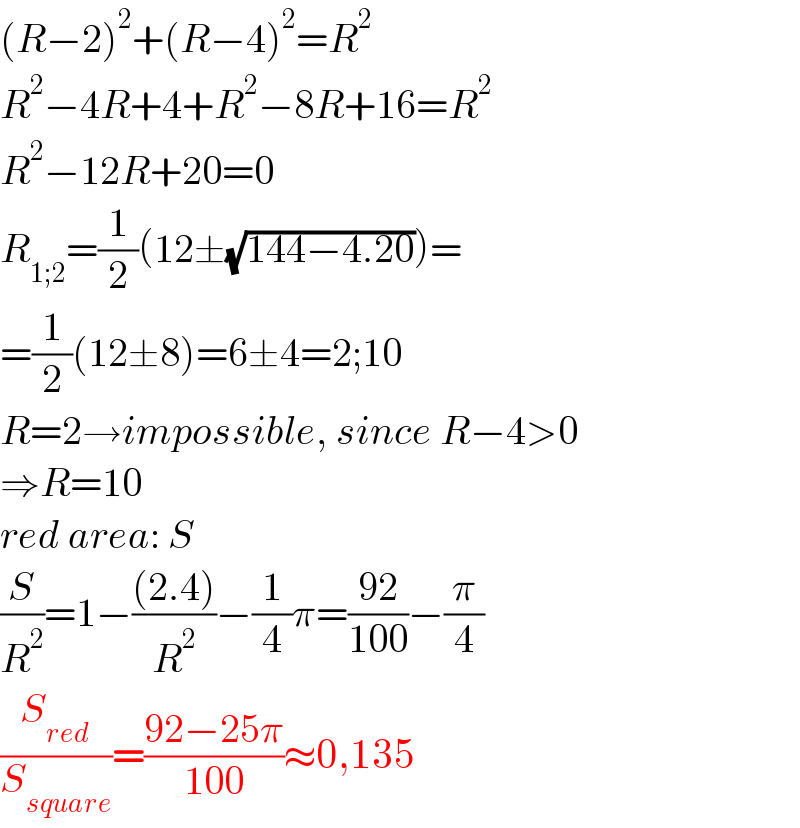
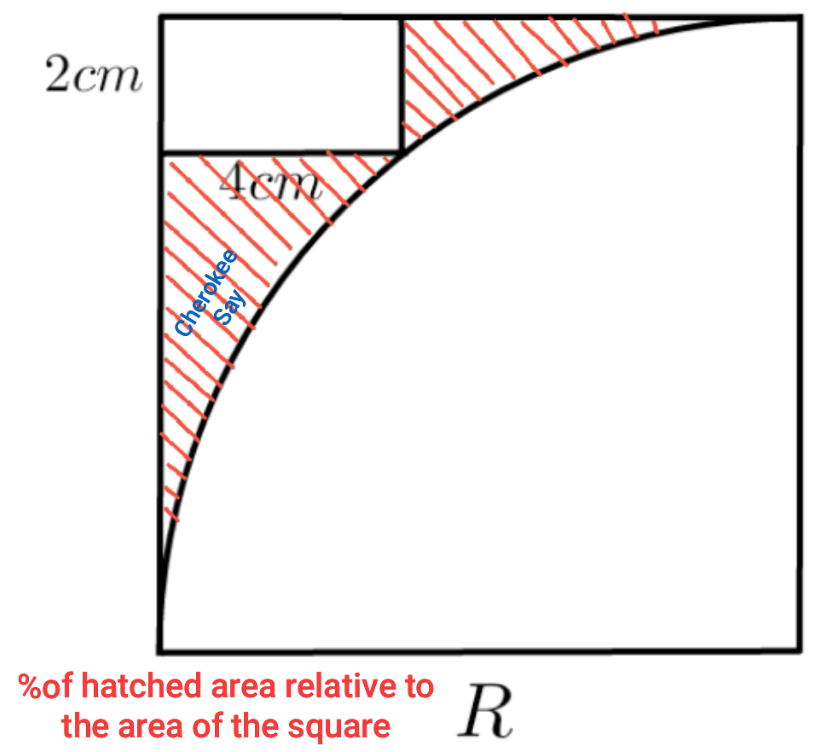
$$\left({R}−\mathrm{2}\right)^{\mathrm{2}} +\left({R}−\mathrm{4}\right)^{\mathrm{2}} ={R}^{\mathrm{2}} \\ $$$${R}^{\mathrm{2}} −\mathrm{4}{R}+\mathrm{4}+{R}^{\mathrm{2}} −\mathrm{8}{R}+\mathrm{16}={R}^{\mathrm{2}} \\ $$$${R}^{\mathrm{2}} −\mathrm{12}{R}+\mathrm{20}=\mathrm{0} \\ $$$${R}_{\mathrm{1};\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{12}\pm\sqrt{\mathrm{144}−\mathrm{4}.\mathrm{20}}\right)= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{12}\pm\mathrm{8}\right)=\mathrm{6}\pm\mathrm{4}=\mathrm{2};\mathrm{10} \\ $$$${R}=\mathrm{2}\rightarrow{impossible},\:{since}\:{R}−\mathrm{4}>\mathrm{0} \\ $$$$\Rightarrow{R}=\mathrm{10} \\ $$$${red}\:{area}:\:{S} \\ $$$$\frac{{S}}{{R}^{\mathrm{2}} }=\mathrm{1}−\frac{\left(\mathrm{2}.\mathrm{4}\right)}{{R}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{4}}\pi=\frac{\mathrm{92}}{\mathrm{100}}−\frac{\pi}{\mathrm{4}} \\ $$$$\frac{{S}_{{red}} }{{S}_{{square}} }=\frac{\mathrm{92}−\mathrm{25}\pi}{\mathrm{100}}\approx\mathrm{0},\mathrm{135} \\ $$
Commented by cherokeesay last updated on 17/Dec/21

$${very}\:{nice}\:!\: \\ $$$${thank}\:{you}\:! \\ $$
Commented by Tawa11 last updated on 18/Dec/21

$$\mathrm{Great}\:\mathrm{sir}. \\ $$
