Question-161578

Question Number 161578 by Ari last updated on 19/Dec/21

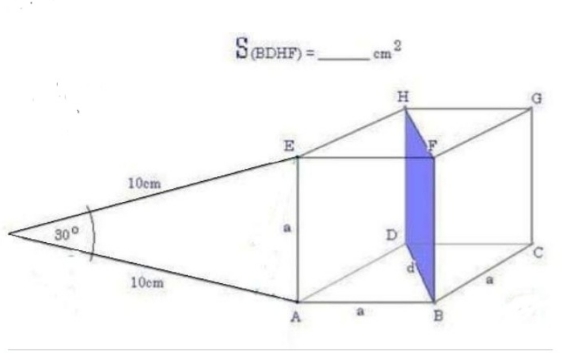
Commented by blackmamba last updated on 20/Dec/21

$$\:\mathrm{cos}\:\mathrm{75}°=\:\frac{\frac{\mathrm{1}}{\mathrm{2}}{a}}{\mathrm{10}}\:=\:\frac{{a}}{\mathrm{20}} \\ $$$$\:\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{2}}\:.\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{3}}\:−\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{2}}\:.\frac{\mathrm{1}}{\mathrm{2}}\:=\:\frac{{a}}{\mathrm{20}} \\ $$$$\:\Rightarrow\sqrt{\mathrm{6}}−\sqrt{\mathrm{2}}\:=\:\frac{{a}}{\mathrm{5}} \\ $$$$\Rightarrow{a}=\mathrm{5}\sqrt{\mathrm{2}}\:\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)\:{cm} \\ $$$$\therefore\:{S}\left[{BDHF}\right]\:=\:{a}^{\mathrm{2}} \sqrt{\mathrm{2}}\:{cm}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{50}\sqrt{\mathrm{2}}\:\left(\mathrm{4}−\mathrm{2}\sqrt{\mathrm{3}}\:\right){cm}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{100}\sqrt{\mathrm{2}}\:\left(\mathrm{2}−\sqrt{\mathrm{3}}\:\right)\:{cm}^{\mathrm{2}} \\ $$

Answered by Rasheed.Sindhi last updated on 20/Dec/21

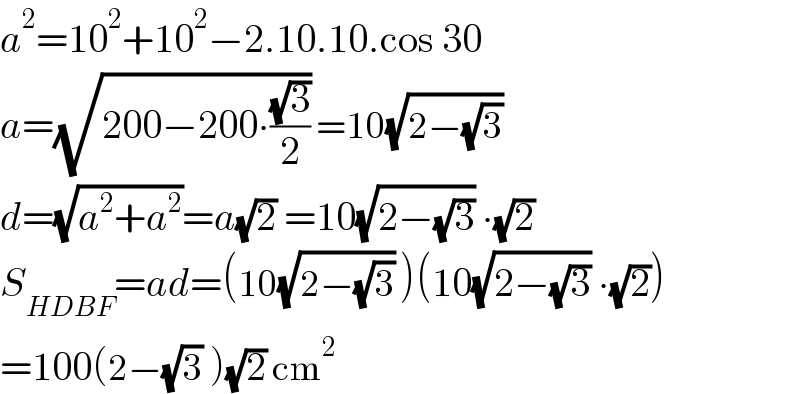
$${a}^{\mathrm{2}} =\mathrm{10}^{\mathrm{2}} +\mathrm{10}^{\mathrm{2}} −\mathrm{2}.\mathrm{10}.\mathrm{10}.\mathrm{cos}\:\mathrm{30} \\ $$$${a}=\sqrt{\mathrm{200}−\mathrm{200}\centerdot\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}\:=\mathrm{10}\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}}\: \\ $$$${d}=\sqrt{{a}^{\mathrm{2}} +{a}^{\mathrm{2}} }={a}\sqrt{\mathrm{2}}\:=\mathrm{10}\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}}\:\centerdot\sqrt{\mathrm{2}}\: \\ $$$${S}_{{HDBF}} ={ad}=\left(\mathrm{10}\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}}\:\right)\left(\mathrm{10}\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}}\:\centerdot\sqrt{\mathrm{2}}\right) \\ $$$$=\mathrm{100}\left(\mathrm{2}−\sqrt{\mathrm{3}}\:\right)\sqrt{\mathrm{2}}\:\mathrm{cm}^{\mathrm{2}} \\ $$

Terms of Service
Privacy Policy
Contact: info@tinkutara.com