Menu Close

Question-161617

Tinku Tara 0 Comments
Pin




Question Number 161617 by gbanda95 last updated on 20/Dec/21
Answered by mathmax by abdo last updated on 20/Dec/21
I_(n+2) =∫_0 ^(π/2) sin^(n+2) dx =∫_0 ^(π/2) (1−cos^2 x)sin^n x dx =I_n −∫_0 ^(π/2) cosx(cosx sin^n x)dx (u=cosx and v^′ =cosx sin^n x) so∫_0 ^(π/2) cosx(cosx sin^n x)dx =[cosx(1/(n+1))sin^(n+1) x]_0 ^(π/2) −∫_0 ^(π/2) (−sinx)((sin^(n+1) x)/(n+1))dx =(1/(n+1))∫_0 ^(π/2) sin^(n+2) xdx =(1/(n+1))I_(n+2) ⇒I_(n+2) =I_n −(1/(n+1))I_(n+2) ⇒ (1+(1/(n+1)))I_(n+2) =I_n ⇒((n+2)/(n+1))I_(n+2) =I_n ⇒I_(n+2) =((n+1)/(n+2))I_n I_0 =∫_0 ^(π/2) dx =(π/2) I_1 =∫_0 ^(π/2) sinxdx=[−cosx]_0 ^(π/2) =1
$$\mathrm{I}_{\mathrm{n}+\mathrm{2}} =\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{sin}^{\mathrm{n}+\mathrm{2}} \mathrm{dx}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \mathrm{x}\right)\mathrm{sin}^{\mathrm{n}} \mathrm{x}\:\mathrm{dx} \\ $$$$=\mathrm{I}_{\mathrm{n}} −\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{cosx}\left(\mathrm{cosx}\:\mathrm{sin}^{\mathrm{n}} \mathrm{x}\right)\mathrm{dx}\:\:\:\:\:\left(\mathrm{u}=\mathrm{cosx}\:\mathrm{and}\:\mathrm{v}^{'} =\mathrm{cosx}\:\mathrm{sin}^{\mathrm{n}} \mathrm{x}\right) \\ $$$$\mathrm{so}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{cosx}\left(\mathrm{cosx}\:\mathrm{sin}^{\mathrm{n}} \mathrm{x}\right)\mathrm{dx}\:=\left[\mathrm{cosx}\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}\mathrm{sin}^{\mathrm{n}+\mathrm{1}} \mathrm{x}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(−\mathrm{sinx}\right)\frac{\mathrm{sin}^{\mathrm{n}+\mathrm{1}} \mathrm{x}}{\mathrm{n}+\mathrm{1}}\mathrm{dx}\:=\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{sin}^{\mathrm{n}+\mathrm{2}} \mathrm{xdx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}\mathrm{I}_{\mathrm{n}+\mathrm{2}} \:\Rightarrow\mathrm{I}_{\mathrm{n}+\mathrm{2}} =\mathrm{I}_{\mathrm{n}} −\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}\mathrm{I}_{\mathrm{n}+\mathrm{2}} \Rightarrow \\ $$$$\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}\right)\mathrm{I}_{\mathrm{n}+\mathrm{2}} =\mathrm{I}_{\mathrm{n}} \:\Rightarrow\frac{\mathrm{n}+\mathrm{2}}{\mathrm{n}+\mathrm{1}}\mathrm{I}_{\mathrm{n}+\mathrm{2}} =\mathrm{I}_{\mathrm{n}} \:\Rightarrow\mathrm{I}_{\mathrm{n}+\mathrm{2}} =\frac{\mathrm{n}+\mathrm{1}}{\mathrm{n}+\mathrm{2}}\mathrm{I}_{\mathrm{n}} \\ $$$$\mathrm{I}_{\mathrm{0}} =\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{dx}\:=\frac{\pi}{\mathrm{2}} \\ $$$$\mathrm{I}_{\mathrm{1}} =\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{sinxdx}=\left[−\mathrm{cosx}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} =\mathrm{1} \\ $$
Answered by mathmax by abdo last updated on 20/Dec/21
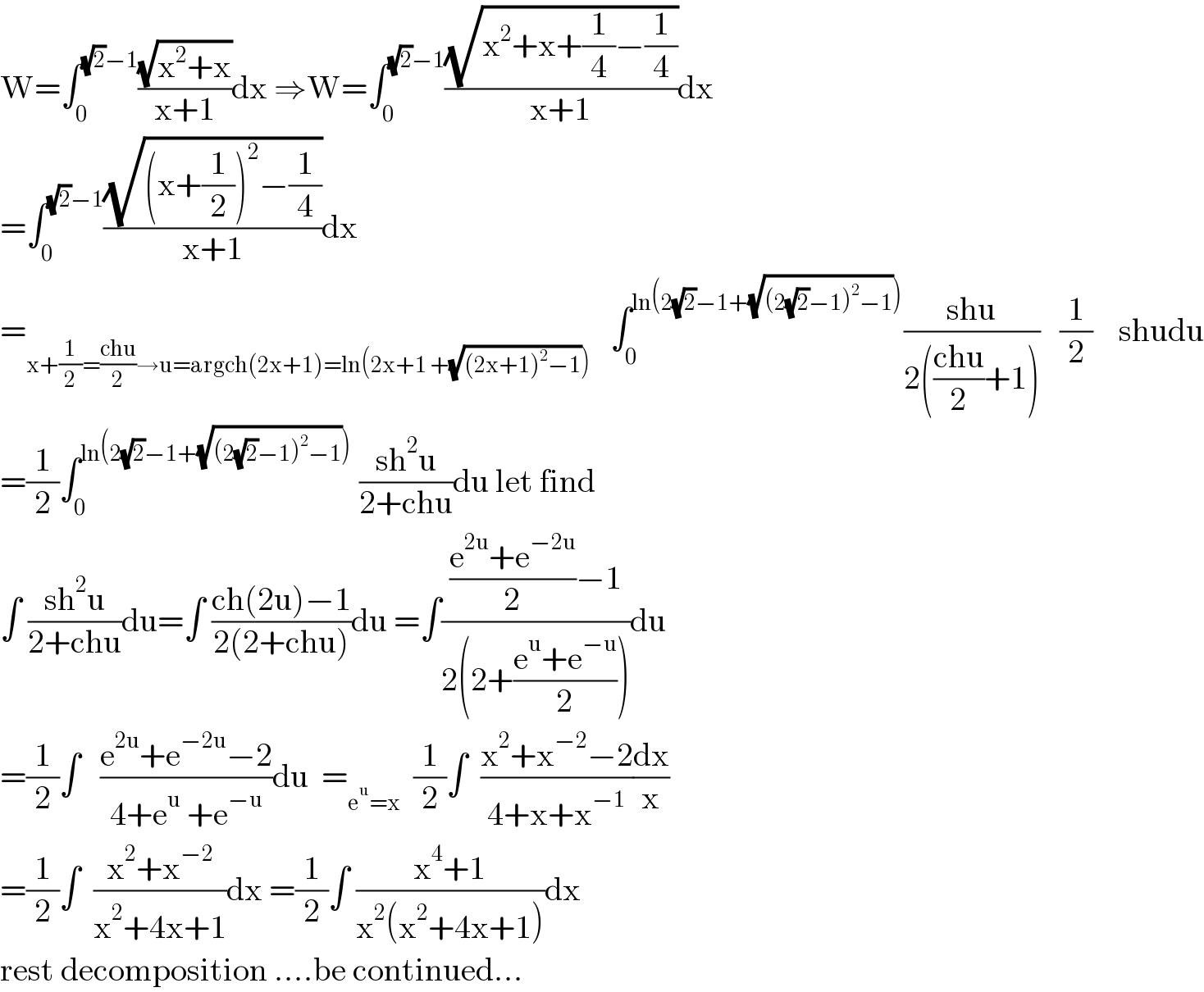
W=∫_0 ^((√2)−1) ((√(x^2 +x))/(x+1))dx ⇒W=∫_0 ^((√2)−1) ((√(x^2 +x+(1/4)−(1/4)))/(x+1))dx =∫_0 ^((√2)−1) ((√((x+(1/2))^2 −(1/4)))/(x+1))dx =_(x+(1/2)=((chu)/2)→u=argch(2x+1)=ln(2x+1 +(√((2x+1)^2 −1)))) ∫_0 ^(ln(2(√2)−1+(√((2(√2)−1)^2 −1)))) ((shu)/(2(((chu)/2)+1))) (1/2) shudu =(1/2)∫_0 ^(ln(2(√2)−1+(√((2(√2)−1)^2 −1)))) ((sh^2 u)/(2+chu))du let find ∫ ((sh^2 u)/(2+chu))du=∫ ((ch(2u)−1)/(2(2+chu)))du =∫((((e^(2u) +e^(−2u) )/2)−1)/(2(2+((e^u +e^(−u) )/2))))du =(1/2)∫ ((e^(2u) +e^(−2u) −2)/(4+e^u +e^(−u) ))du =_(e^u =x) (1/2)∫ ((x^2 +x^(−2) −2)/(4+x+x^(−1) ))(dx/x) =(1/2)∫ ((x^2 +x^(−2) )/(x^2 +4x+1))dx =(1/2)∫ ((x^4 +1)/(x^2 (x^2 +4x+1)))dx rest decomposition ....be continued...
$$\mathrm{W}=\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \frac{\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}}}{\mathrm{x}+\mathrm{1}}\mathrm{dx}\:\Rightarrow\mathrm{W}=\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \frac{\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{4}}}}{\mathrm{x}+\mathrm{1}}\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \frac{\sqrt{\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}}}{\mathrm{x}+\mathrm{1}}\mathrm{dx} \\ $$$$=_{\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{chu}}{\mathrm{2}}\rightarrow\mathrm{u}=\mathrm{argch}\left(\mathrm{2x}+\mathrm{1}\right)=\mathrm{ln}\left(\mathrm{2x}+\mathrm{1}\:+\sqrt{\left(\mathrm{2x}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{1}}\right)} \:\:\:\int_{\mathrm{0}} ^{\mathrm{ln}\left(\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{1}+\sqrt{\left(\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{1}}\right)} \frac{\mathrm{shu}}{\mathrm{2}\left(\frac{\mathrm{chu}}{\mathrm{2}}+\mathrm{1}\right)}\:\:\:\frac{\mathrm{1}}{\mathrm{2}}\:\:\:\:\mathrm{shudu} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{ln}\left(\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{1}+\sqrt{\left(\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{1}}\right)} \:\frac{\mathrm{sh}^{\mathrm{2}} \mathrm{u}}{\mathrm{2}+\mathrm{chu}}\mathrm{du}\:\mathrm{let}\:\mathrm{find} \\ $$$$\int\:\frac{\mathrm{sh}^{\mathrm{2}} \mathrm{u}}{\mathrm{2}+\mathrm{chu}}\mathrm{du}=\int\:\frac{\mathrm{ch}\left(\mathrm{2u}\right)−\mathrm{1}}{\mathrm{2}\left(\mathrm{2}+\mathrm{chu}\right)}\mathrm{du}\:=\int\frac{\frac{\mathrm{e}^{\mathrm{2u}} +\mathrm{e}^{−\mathrm{2u}} }{\mathrm{2}}−\mathrm{1}}{\mathrm{2}\left(\mathrm{2}+\frac{\mathrm{e}^{\mathrm{u}} +\mathrm{e}^{−\mathrm{u}} }{\mathrm{2}}\right)}\mathrm{du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\:\:\:\frac{\mathrm{e}^{\mathrm{2u}} +\mathrm{e}^{−\mathrm{2u}} −\mathrm{2}}{\mathrm{4}+\mathrm{e}^{\mathrm{u}} \:+\mathrm{e}^{−\mathrm{u}} }\mathrm{du}\:\:=_{\mathrm{e}^{\mathrm{u}} =\mathrm{x}} \:\:\frac{\mathrm{1}}{\mathrm{2}}\int\:\:\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{x}^{−\mathrm{2}} −\mathrm{2}}{\mathrm{4}+\mathrm{x}+\mathrm{x}^{−\mathrm{1}} }\frac{\mathrm{dx}}{\mathrm{x}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\:\:\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{x}^{−\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} +\mathrm{4x}+\mathrm{1}}\mathrm{dx}\:=\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{\mathrm{x}^{\mathrm{4}} +\mathrm{1}}{\mathrm{x}^{\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} +\mathrm{4x}+\mathrm{1}\right)}\mathrm{dx} \\ $$$$\mathrm{rest}\:\mathrm{decomposition}\:….\mathrm{be}\:\mathrm{continued}… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *