Question Number 161626 by ZiYangLee last updated on 20/Dec/21

Commented by TheSupreme last updated on 20/Dec/21
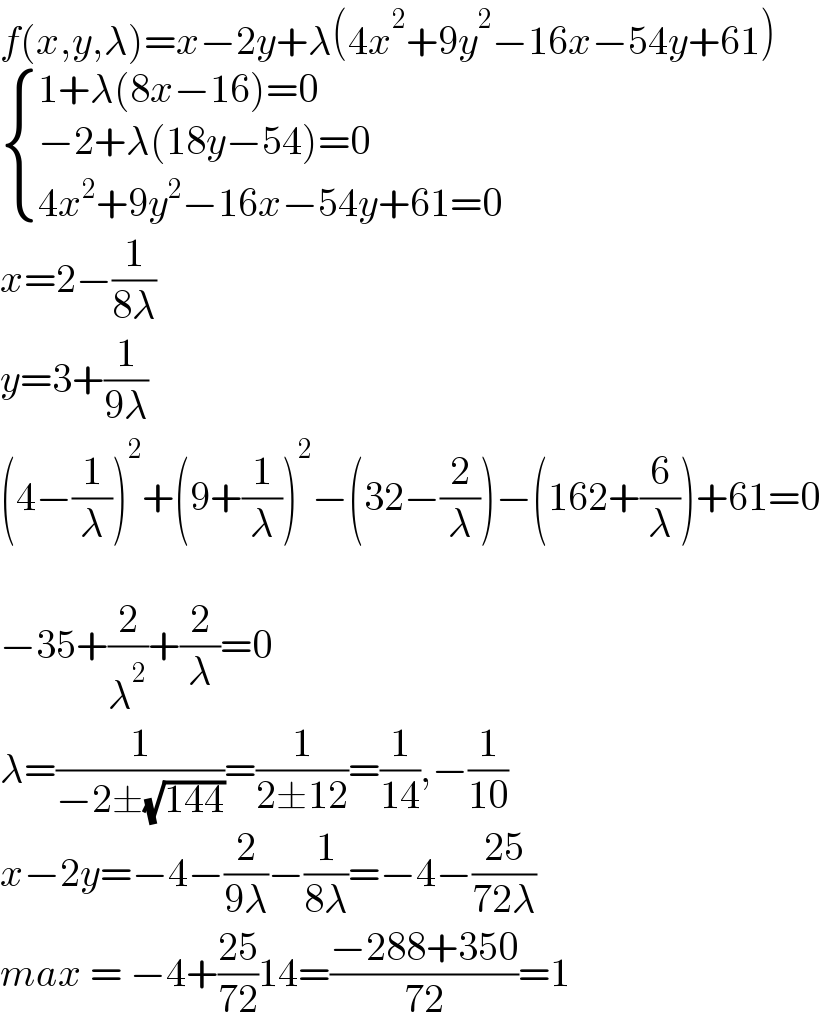
$${f}\left({x},{y},\lambda\right)={x}−\mathrm{2}{y}+\lambda\left(\mathrm{4}{x}^{\mathrm{2}} +\mathrm{9}{y}^{\mathrm{2}} −\mathrm{16}{x}−\mathrm{54}{y}+\mathrm{61}\right) \\ $$$$\begin{cases}{\mathrm{1}+\lambda\left(\mathrm{8}{x}−\mathrm{16}\right)=\mathrm{0}}\\{−\mathrm{2}+\lambda\left(\mathrm{18}{y}−\mathrm{54}\right)=\mathrm{0}}\\{\mathrm{4}{x}^{\mathrm{2}} +\mathrm{9}{y}^{\mathrm{2}} −\mathrm{16}{x}−\mathrm{54}{y}+\mathrm{61}=\mathrm{0}}\end{cases} \\ $$$${x}=\mathrm{2}−\frac{\mathrm{1}}{\mathrm{8}\lambda} \\ $$$${y}=\mathrm{3}+\frac{\mathrm{1}}{\mathrm{9}\lambda} \\ $$$$\left(\mathrm{4}−\frac{\mathrm{1}}{\lambda}\right)^{\mathrm{2}} +\left(\mathrm{9}+\frac{\mathrm{1}}{\lambda}\right)^{\mathrm{2}} −\left(\mathrm{32}−\frac{\mathrm{2}}{\lambda}\right)−\left(\mathrm{162}+\frac{\mathrm{6}}{\lambda}\right)+\mathrm{61}=\mathrm{0} \\ $$$$ \\ $$$$−\mathrm{35}+\frac{\mathrm{2}}{\lambda^{\mathrm{2}} }+\frac{\mathrm{2}}{\lambda}=\mathrm{0} \\ $$$$\lambda=\frac{\mathrm{1}}{−\mathrm{2}\pm\sqrt{\mathrm{144}}}=\frac{\mathrm{1}}{\mathrm{2}\pm\mathrm{12}}=\frac{\mathrm{1}}{\mathrm{14}},−\frac{\mathrm{1}}{\mathrm{10}} \\ $$$${x}−\mathrm{2}{y}=−\mathrm{4}−\frac{\mathrm{2}}{\mathrm{9}\lambda}−\frac{\mathrm{1}}{\mathrm{8}\lambda}=−\mathrm{4}−\frac{\mathrm{25}}{\mathrm{72}\lambda} \\ $$$${max}\:=\:−\mathrm{4}+\frac{\mathrm{25}}{\mathrm{72}}\mathrm{14}=\frac{−\mathrm{288}+\mathrm{350}}{\mathrm{72}}=\mathrm{1} \\ $$
Answered by mr W last updated on 20/Dec/21
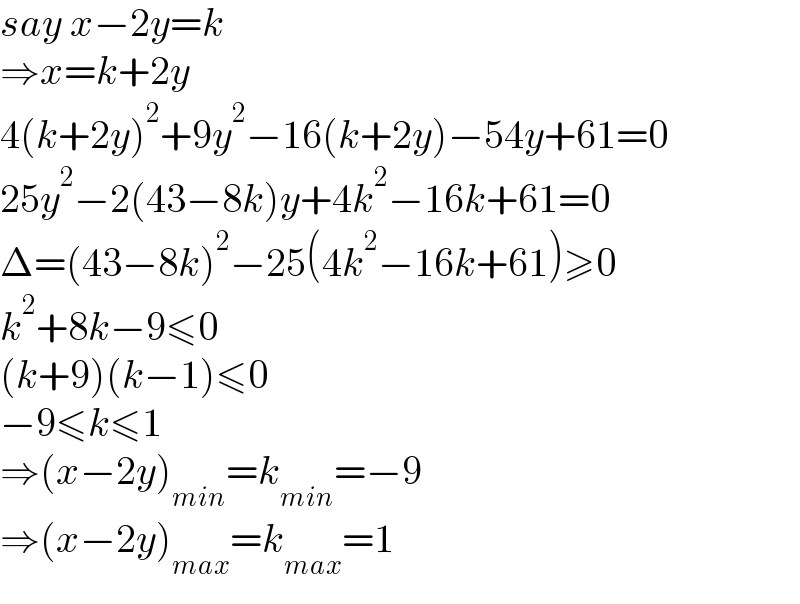
$${say}\:{x}−\mathrm{2}{y}={k} \\ $$$$\Rightarrow{x}={k}+\mathrm{2}{y} \\ $$$$\mathrm{4}\left({k}+\mathrm{2}{y}\right)^{\mathrm{2}} +\mathrm{9}{y}^{\mathrm{2}} −\mathrm{16}\left({k}+\mathrm{2}{y}\right)−\mathrm{54}{y}+\mathrm{61}=\mathrm{0} \\ $$$$\mathrm{25}{y}^{\mathrm{2}} −\mathrm{2}\left(\mathrm{43}−\mathrm{8}{k}\right){y}+\mathrm{4}{k}^{\mathrm{2}} −\mathrm{16}{k}+\mathrm{61}=\mathrm{0} \\ $$$$\Delta=\left(\mathrm{43}−\mathrm{8}{k}\right)^{\mathrm{2}} −\mathrm{25}\left(\mathrm{4}{k}^{\mathrm{2}} −\mathrm{16}{k}+\mathrm{61}\right)\geqslant\mathrm{0} \\ $$$${k}^{\mathrm{2}} +\mathrm{8}{k}−\mathrm{9}\leqslant\mathrm{0} \\ $$$$\left({k}+\mathrm{9}\right)\left({k}−\mathrm{1}\right)\leqslant\mathrm{0} \\ $$$$−\mathrm{9}\leqslant{k}\leqslant\mathrm{1} \\ $$$$\Rightarrow\left({x}−\mathrm{2}{y}\right)_{{min}} ={k}_{{min}} =−\mathrm{9} \\ $$$$\Rightarrow\left({x}−\mathrm{2}{y}\right)_{{max}} ={k}_{{max}} =\mathrm{1} \\ $$
Commented by mr W last updated on 20/Dec/21
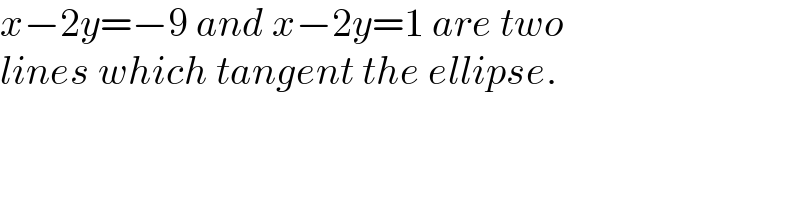
$${x}−\mathrm{2}{y}=−\mathrm{9}\:{and}\:{x}−\mathrm{2}{y}=\mathrm{1}\:{are}\:{two} \\ $$$${lines}\:{which}\:{tangent}\:{the}\:{ellipse}. \\ $$
Commented by mr W last updated on 20/Dec/21

Commented by ZiYangLee last updated on 20/Dec/21

$$\mathrm{Thank}\:\mathrm{you}\:! \\ $$
Answered by aleks041103 last updated on 20/Dec/21
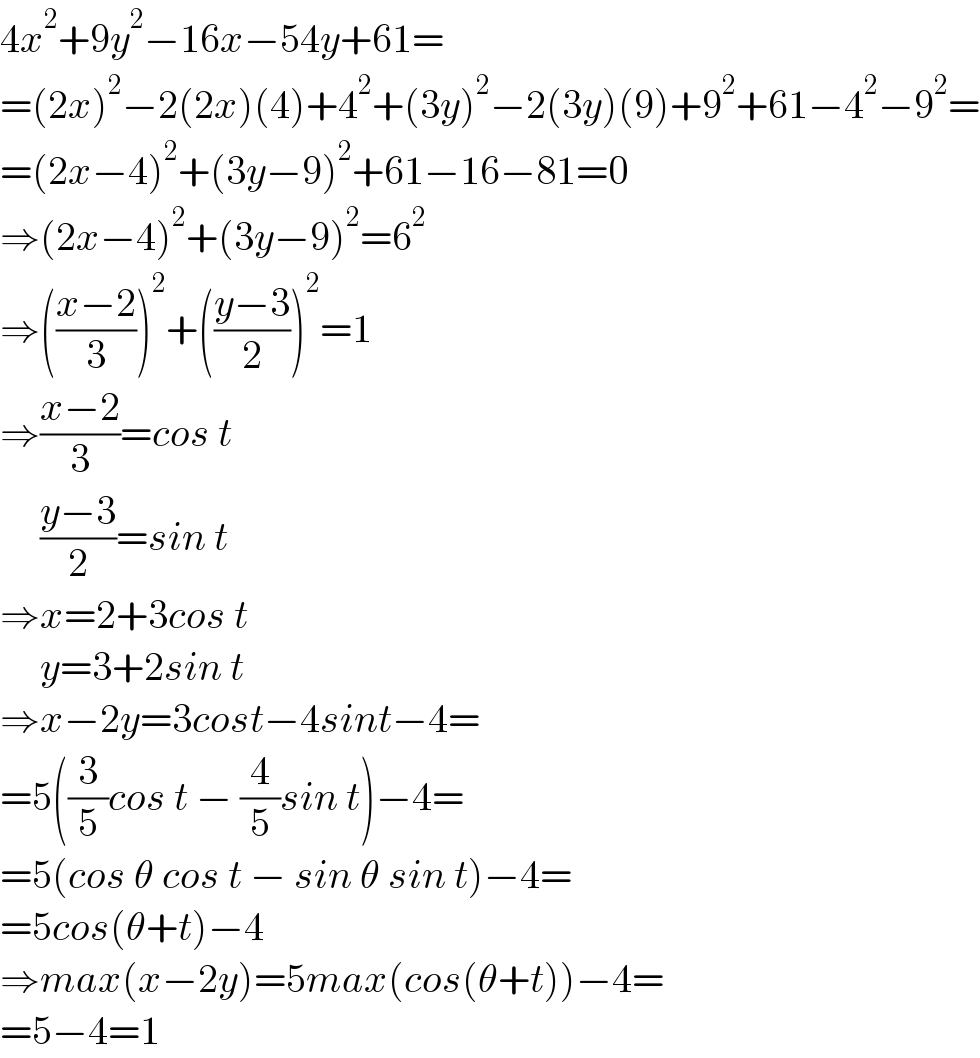
$$\mathrm{4}{x}^{\mathrm{2}} +\mathrm{9}{y}^{\mathrm{2}} −\mathrm{16}{x}−\mathrm{54}{y}+\mathrm{61}= \\ $$$$=\left(\mathrm{2}{x}\right)^{\mathrm{2}} −\mathrm{2}\left(\mathrm{2}{x}\right)\left(\mathrm{4}\right)+\mathrm{4}^{\mathrm{2}} +\left(\mathrm{3}{y}\right)^{\mathrm{2}} −\mathrm{2}\left(\mathrm{3}{y}\right)\left(\mathrm{9}\right)+\mathrm{9}^{\mathrm{2}} +\mathrm{61}−\mathrm{4}^{\mathrm{2}} −\mathrm{9}^{\mathrm{2}} = \\ $$$$=\left(\mathrm{2}{x}−\mathrm{4}\right)^{\mathrm{2}} +\left(\mathrm{3}{y}−\mathrm{9}\right)^{\mathrm{2}} +\mathrm{61}−\mathrm{16}−\mathrm{81}=\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{2}{x}−\mathrm{4}\right)^{\mathrm{2}} +\left(\mathrm{3}{y}−\mathrm{9}\right)^{\mathrm{2}} =\mathrm{6}^{\mathrm{2}} \\ $$$$\Rightarrow\left(\frac{{x}−\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{2}} +\left(\frac{{y}−\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} =\mathrm{1} \\ $$$$\Rightarrow\frac{{x}−\mathrm{2}}{\mathrm{3}}={cos}\:{t} \\ $$$$\:\:\:\:\:\frac{{y}−\mathrm{3}}{\mathrm{2}}={sin}\:{t} \\ $$$$\Rightarrow{x}=\mathrm{2}+\mathrm{3}{cos}\:{t} \\ $$$$\:\:\:\:\:{y}=\mathrm{3}+\mathrm{2}{sin}\:{t} \\ $$$$\Rightarrow{x}−\mathrm{2}{y}=\mathrm{3}{cost}−\mathrm{4}{sint}−\mathrm{4}= \\ $$$$=\mathrm{5}\left(\frac{\mathrm{3}}{\mathrm{5}}{cos}\:{t}\:−\:\frac{\mathrm{4}}{\mathrm{5}}{sin}\:{t}\right)−\mathrm{4}= \\ $$$$=\mathrm{5}\left({cos}\:\theta\:{cos}\:{t}\:−\:{sin}\:\theta\:{sin}\:{t}\right)−\mathrm{4}= \\ $$$$=\mathrm{5}{cos}\left(\theta+{t}\right)−\mathrm{4} \\ $$$$\Rightarrow{max}\left({x}−\mathrm{2}{y}\right)=\mathrm{5}{max}\left({cos}\left(\theta+{t}\right)\right)−\mathrm{4}= \\ $$$$=\mathrm{5}−\mathrm{4}=\mathrm{1} \\ $$
Commented by peter frank last updated on 20/Dec/21

$$\mathrm{thank}\:\mathrm{you} \\ $$
Answered by mr W last updated on 20/Dec/21
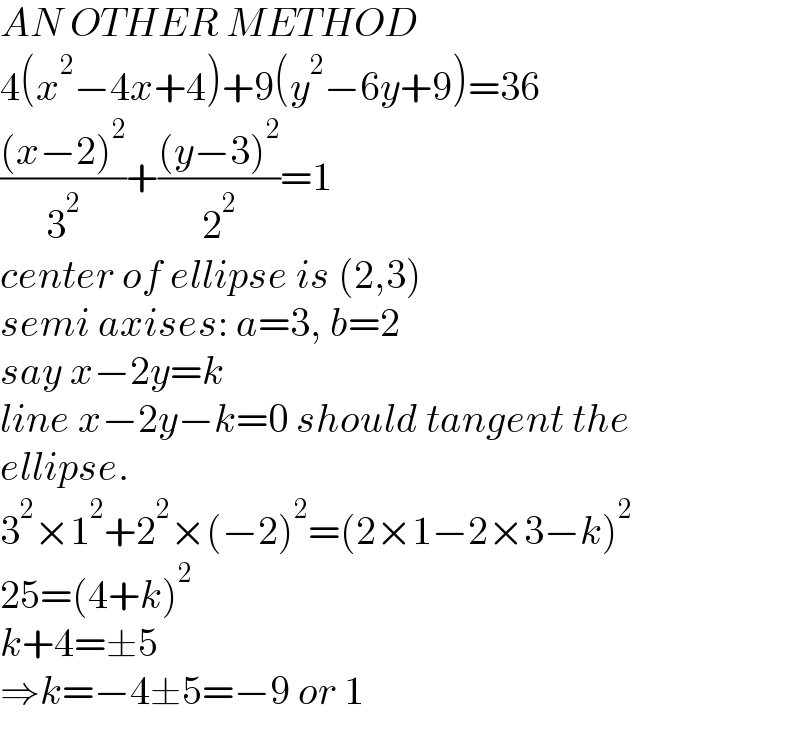
$${AN}\:{OTHER}\:{METHOD} \\ $$$$\mathrm{4}\left({x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{4}\right)+\mathrm{9}\left({y}^{\mathrm{2}} −\mathrm{6}{y}+\mathrm{9}\right)=\mathrm{36} \\ $$$$\frac{\left({x}−\mathrm{2}\right)^{\mathrm{2}} }{\mathrm{3}^{\mathrm{2}} }+\frac{\left({y}−\mathrm{3}\right)^{\mathrm{2}} }{\mathrm{2}^{\mathrm{2}} }=\mathrm{1} \\ $$$${center}\:{of}\:{ellipse}\:{is}\:\left(\mathrm{2},\mathrm{3}\right) \\ $$$${semi}\:{axises}:\:{a}=\mathrm{3},\:{b}=\mathrm{2} \\ $$$${say}\:{x}−\mathrm{2}{y}={k} \\ $$$${line}\:{x}−\mathrm{2}{y}−{k}=\mathrm{0}\:{should}\:{tangent}\:{the} \\ $$$${ellipse}. \\ $$$$\mathrm{3}^{\mathrm{2}} ×\mathrm{1}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} ×\left(−\mathrm{2}\right)^{\mathrm{2}} =\left(\mathrm{2}×\mathrm{1}−\mathrm{2}×\mathrm{3}−{k}\right)^{\mathrm{2}} \\ $$$$\mathrm{25}=\left(\mathrm{4}+{k}\right)^{\mathrm{2}} \\ $$$${k}+\mathrm{4}=\pm\mathrm{5} \\ $$$$\Rightarrow{k}=−\mathrm{4}\pm\mathrm{5}=−\mathrm{9}\:{or}\:\mathrm{1} \\ $$
Commented by peter frank last updated on 20/Dec/21

$$\mathrm{thank}\:\mathrm{you} \\ $$
