Question Number 161668 by mnjuly1970 last updated on 21/Dec/21
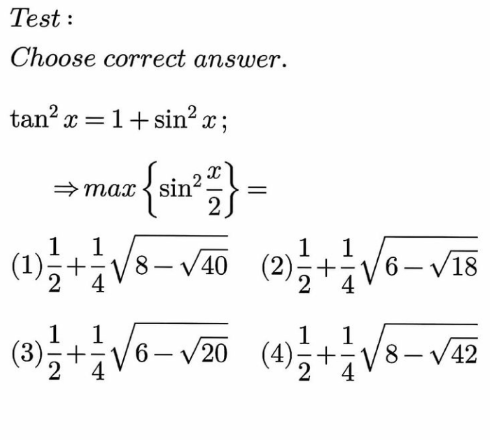
Answered by mr W last updated on 21/Dec/21

$$\frac{\mathrm{sin}^{\mathrm{2}} \:{x}}{\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \:{x}}=\mathrm{1}+\mathrm{sin}^{\mathrm{2}} \:{x} \\ $$$$\mathrm{sin}^{\mathrm{4}} \:{x}+\mathrm{sin}^{\mathrm{2}} \:{x}−\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{sin}^{\mathrm{2}} \:{x}=\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}=\phi \\ $$$$\mathrm{4}\:\mathrm{sin}^{\mathrm{2}} \:\frac{{x}}{\mathrm{2}}\left(\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \:\frac{{x}}{\mathrm{2}}\right)=\phi \\ $$$$\mathrm{sin}^{\mathrm{4}} \:\frac{{x}}{\mathrm{2}}−\mathrm{sin}^{\mathrm{2}} \:\frac{{x}}{\mathrm{2}}+\frac{\phi}{\mathrm{4}}=\mathrm{0} \\ $$$$\mathrm{sin}^{\mathrm{2}} \:\frac{{x}}{\mathrm{2}}=\frac{\mathrm{1}\pm\sqrt{\mathrm{1}−\phi}}{\mathrm{2}} \\ $$$$\left(\mathrm{sin}^{\mathrm{2}} \:\frac{{x}}{\mathrm{2}}\right)_{{max}} =\frac{\mathrm{1}+\sqrt{\mathrm{1}−\phi}}{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}+\sqrt{\frac{\mathrm{3}−\sqrt{\mathrm{5}}}{\mathrm{2}}}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{6}−\mathrm{2}\sqrt{\mathrm{5}}}}{\mathrm{4}}=\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{4}}=\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{2}} \\ $$$$ \\ $$$$\frac{\sqrt{\mathrm{6}−\mathrm{2}\sqrt{\mathrm{5}}}}{\mathrm{4}}=\frac{\sqrt{\mathrm{6}−\sqrt{\mathrm{20}}}}{\mathrm{4}} \\ $$$$\Rightarrow{answer}\:\left(\mathrm{3}\right)\:{is}\:{correct}: \\ $$
Commented by mnjuly1970 last updated on 21/Dec/21
$${geateful}\:{sir}\:{W}…{very}\:{excellent} \\ $$
