Question Number 161742 by mr W last updated on 21/Dec/21
Commented by mr W last updated on 21/Dec/21
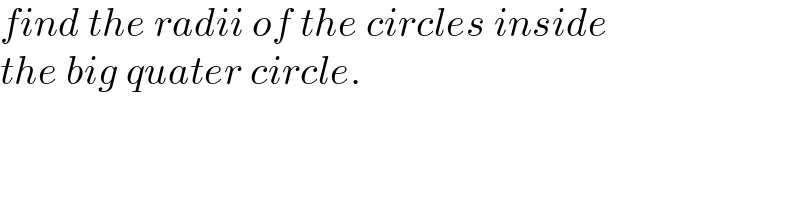
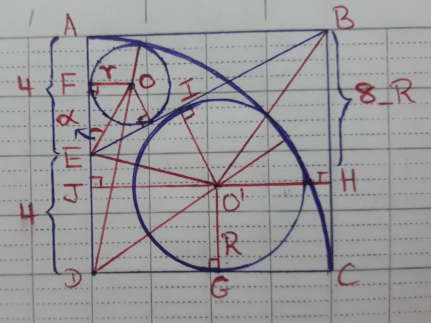
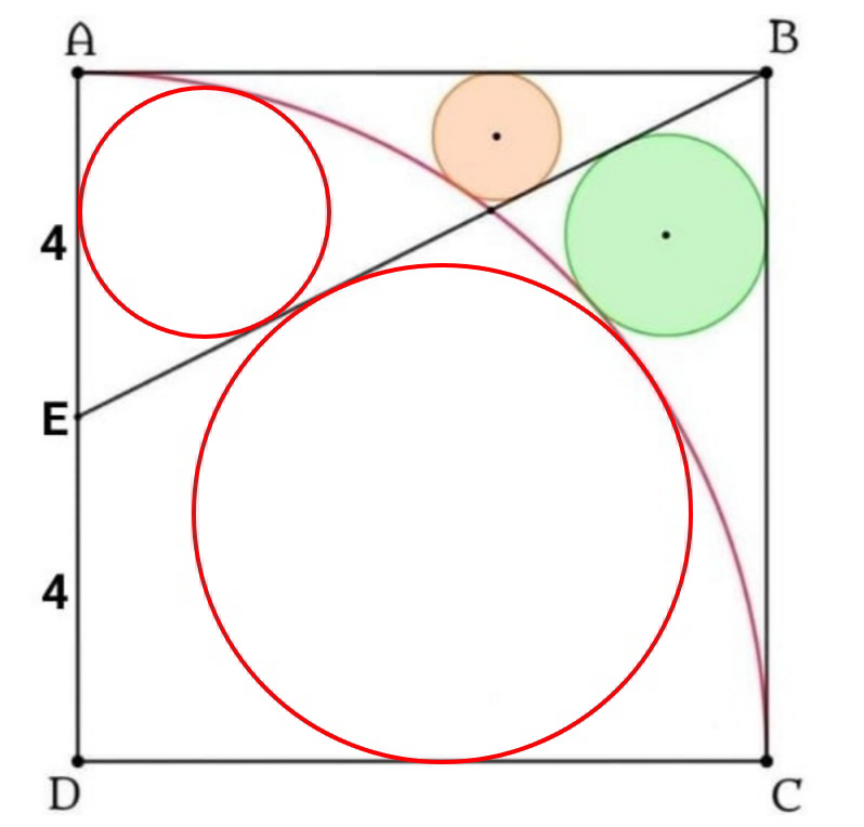
$${find}\:{the}\:{radii}\:{of}\:{the}\:{circles}\:{inside} \\ $$$${the}\:{big}\:{quater}\:{circle}. \\ $$
Answered by FongXD last updated on 22/Dec/21

$$\begin{array}{|c|}{\mathrm{Find}\:\mathrm{the}\:\mathrm{radius}\:\left(\mathrm{r}\right)\:\mathrm{of}\:\mathrm{the}\:\mathrm{small}\:\mathrm{circle}}\\\hline\end{array}: \\ $$$$\bullet\:\mathrm{tan2}\alpha=\frac{\mathrm{8}}{\mathrm{4}}=\mathrm{2}=\frac{\mathrm{2tan}\alpha}{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \alpha},\:\mathrm{but}\:\mathrm{tan}\alpha=\frac{\mathrm{r}}{\mathrm{FE}} \\ $$$$\Leftrightarrow\:\frac{\mathrm{2r}\left(\mathrm{FE}\right)}{\left(\mathrm{FE}\right)^{\mathrm{2}} −\mathrm{r}^{\mathrm{2}} }=\mathrm{2},\:\Leftrightarrow\:\left(\mathrm{FE}\right)^{\mathrm{2}} −\mathrm{r}\left(\mathrm{FE}\right)−\mathrm{r}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{FE}=\mathrm{r}\left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right) \\ $$$$\blacktriangle\:\mathrm{in}\:\mathrm{the}\:\mathrm{right}\:\mathrm{triangle}\:\mathrm{OFD}: \\ $$$$\bullet\:\mathrm{FD}^{\mathrm{2}} =\mathrm{OD}^{\mathrm{2}} −\mathrm{OF}^{\mathrm{2}} \\ $$$$\Leftrightarrow\:\mathrm{FD}=\sqrt{\left(\mathrm{8}−\mathrm{r}\right)^{\mathrm{2}} −\mathrm{r}^{\mathrm{2}} } \\ $$$$\Leftrightarrow\:\mathrm{4}+\mathrm{FE}=\mathrm{4}+\mathrm{r}\left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)=\sqrt{\mathrm{64}−\mathrm{16r}} \\ $$$$\Leftrightarrow\:\mathrm{64}+\mathrm{16r}\left(\mathrm{1}+\sqrt{\mathrm{5}}\right)+\mathrm{r}^{\mathrm{2}} \left(\mathrm{6}+\mathrm{2}\sqrt{\mathrm{5}}\right)=\mathrm{256}−\mathrm{64r} \\ $$$$\Leftrightarrow\:\left(\mathrm{3}+\sqrt{\mathrm{5}}\right)\mathrm{r}^{\mathrm{2}} +\mathrm{8r}\left(\mathrm{5}+\sqrt{\mathrm{5}}\right)−\mathrm{96}=\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{r}=\frac{−\mathrm{4}\left(\mathrm{5}+\sqrt{\mathrm{5}}\right)+\sqrt{\mathrm{16}\left(\mathrm{30}+\mathrm{10}\sqrt{\mathrm{5}}\right)+\mathrm{96}\left(\mathrm{3}+\sqrt{\mathrm{5}}\right)}}{\mathrm{3}+\sqrt{\mathrm{5}}} \\ $$$$\Rightarrow\:\mathrm{r}=\frac{−\mathrm{4}\left(\mathrm{5}+\sqrt{\mathrm{5}}\right)+\mathrm{4}\sqrt{\mathrm{48}+\mathrm{16}\sqrt{\mathrm{5}}}}{\mathrm{9}−\mathrm{5}}×\left(\mathrm{3}−\sqrt{\mathrm{5}}\right) \\ $$$$\Rightarrow\:\mathrm{r}=\left(\mathrm{5}+\sqrt{\mathrm{5}}\right)\left(\sqrt{\mathrm{5}}−\mathrm{3}\right)+\mathrm{4}\left(\mathrm{3}−\sqrt{\mathrm{5}}\right)\sqrt{\mathrm{3}+\sqrt{\mathrm{5}}} \\ $$$$\Rightarrow\:\mathrm{r}=\mathrm{2}\sqrt{\mathrm{5}}−\mathrm{10}+\left(\mathrm{12}−\mathrm{4}\sqrt{\mathrm{5}}\right)\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\:\sqrt{\mathrm{2}}} \\ $$$$\Rightarrow\:\mathrm{r}=\mathrm{2}\sqrt{\mathrm{5}}−\mathrm{10}+\frac{\mathrm{8}\sqrt{\mathrm{5}}−\mathrm{8}}{\:\sqrt{\mathrm{2}}} \\ $$$$\mathrm{therefore},\:\begin{array}{|c|}{\mathrm{r}=\mathrm{4}\sqrt{\mathrm{10}}+\mathrm{2}\sqrt{\mathrm{5}}−\mathrm{4}\sqrt{\mathrm{2}}−\mathrm{10}}\\\hline\end{array} \\ $$$$\begin{array}{|c|}{\mathrm{Find}\:\mathrm{the}\:\mathrm{radius}\:\left(\mathrm{R}\right)\:\mathrm{of}\:\mathrm{the}\:\mathrm{big}\:\mathrm{circle}}\\\hline\end{array}: \\ $$$$\blacktriangle\:\mathrm{in}\:\mathrm{the}\:\mathrm{right}\:\mathrm{triangle}\:\mathrm{O}'\mathrm{DG}: \\ $$$$\bullet\:\mathrm{DG}^{\mathrm{2}} =\mathrm{O}'\mathrm{D}^{\mathrm{2}} −\mathrm{O}'\mathrm{R}^{\mathrm{2}} \\ $$$$\Rightarrow\:\mathrm{DG}=\sqrt{\left(\mathrm{8}−\mathrm{R}\right)^{\mathrm{2}} −\mathrm{R}^{\mathrm{2}} }=\mathrm{4}\sqrt{\mathrm{4}−\mathrm{R}} \\ $$$$\bullet\:\mathrm{O}'\mathrm{H}=\mathrm{CG}=\mathrm{8}−\mathrm{DG}=\mathrm{8}−\mathrm{4}\sqrt{\mathrm{4}−\mathrm{R}} \\ $$$$\blacktriangle\:\mathrm{in}\:\mathrm{the}\:\mathrm{right}\:\mathrm{triangle}\:\mathrm{O}'\mathrm{JE}: \\ $$$$\bullet\:\mathrm{O}'\mathrm{E}^{\mathrm{2}} =\mathrm{O}'\mathrm{J}^{\mathrm{2}} +\mathrm{JE}^{\mathrm{2}} \\ $$$$\Leftrightarrow\:\mathrm{O}'\mathrm{E}^{\mathrm{2}} =\left(\mathrm{4}\sqrt{\mathrm{4}−\mathrm{R}}\right)^{\mathrm{2}} +\left(\mathrm{4}−\mathrm{R}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:\mathrm{O}'\mathrm{E}^{\mathrm{2}} =\mathrm{R}^{\mathrm{2}} −\mathrm{24R}+\mathrm{80} \\ $$$$\blacktriangle\:\mathrm{in}\:\mathrm{the}\:\mathrm{right}\:\mathrm{triangle}\:\mathrm{O}'\mathrm{IE}: \\ $$$$\bullet\:\mathrm{EI}^{\mathrm{2}} =\mathrm{O}'\mathrm{E}^{\mathrm{2}} −\mathrm{O}'\mathrm{I}^{\mathrm{2}} \\ $$$$\Rightarrow\:\mathrm{EI}=\sqrt{\left(\mathrm{R}^{\mathrm{2}} −\mathrm{24R}+\mathrm{80}\right)−\mathrm{R}^{\mathrm{2}} }=\sqrt{\mathrm{80}−\mathrm{24R}} \\ $$$$\blacktriangle\:\mathrm{in}\:\mathrm{the}\:\mathrm{right}\:\mathrm{triangle}\:\mathrm{ABE}: \\ $$$$\bullet\:\mathrm{BE}^{\mathrm{2}} =\mathrm{AB}^{\mathrm{2}} +\mathrm{AE}^{\mathrm{2}} \\ $$$$\Rightarrow\:\mathrm{BE}=\sqrt{\mathrm{8}^{\mathrm{2}} +\mathrm{4}^{\mathrm{2}} }=\mathrm{4}\sqrt{\mathrm{5}} \\ $$$$\bullet\:\mathrm{IB}=\mathrm{BE}−\mathrm{EI}=\mathrm{4}\sqrt{\mathrm{5}}−\sqrt{\mathrm{80}−\mathrm{24R}} \\ $$$$\blacktriangle\:\mathrm{in}\:\mathrm{the}\:\mathrm{right}\:\mathrm{triangle}\:\mathrm{O}'\mathrm{BI}\:\mathrm{and}\:\mathrm{O}'\mathrm{BH} \\ $$$$\bullet\:\mathrm{O}'\mathrm{I}^{\mathrm{2}} +\mathrm{IB}^{\mathrm{2}} =\mathrm{O}'\mathrm{H}^{\mathrm{2}} +\mathrm{HB}^{\mathrm{2}} \\ $$$$\Leftrightarrow\:\mathrm{R}^{\mathrm{2}} +\left(\mathrm{4}\sqrt{\mathrm{5}}−\sqrt{\mathrm{80}−\mathrm{24R}}\right)^{\mathrm{2}} =\left(\mathrm{8}−\mathrm{4}\sqrt{\mathrm{4}−\mathrm{R}}\right)^{\mathrm{2}} +\left(\mathrm{8}−\mathrm{R}\right)^{\mathrm{2}} \\ $$$$\Leftrightarrow\:\mathrm{R}^{\mathrm{2}} +\left(\mathrm{160}−\mathrm{24R}−\mathrm{16}\sqrt{\mathrm{100}−\mathrm{30R}}\right)=\left(\mathrm{128}−\mathrm{16R}−\mathrm{64}\sqrt{\mathrm{4}−\mathrm{R}}\right)+\left(\mathrm{R}^{\mathrm{2}} −\mathrm{16R}+\mathrm{64}\right) \\ $$$$\Leftrightarrow\:\mathrm{R}−\mathrm{4}=\mathrm{2}\sqrt{\mathrm{100}−\mathrm{30R}}−\mathrm{8}\sqrt{\mathrm{4}−\mathrm{R}} \\ $$$$\Leftrightarrow\:\mathrm{R}^{\mathrm{2}} −\mathrm{8R}+\mathrm{16}=\mathrm{656}−\mathrm{184R}−\mathrm{32}\sqrt{\mathrm{30R}^{\mathrm{2}} −\mathrm{220R}+\mathrm{400}} \\ $$$$\Leftrightarrow\:\mathrm{R}^{\mathrm{2}} +\mathrm{176R}−\mathrm{640}=−\mathrm{32}\sqrt{\mathrm{30R}^{\mathrm{2}} −\mathrm{220R}+\mathrm{400}} \\ $$$$\Leftrightarrow\:\mathrm{R}^{\mathrm{4}} +\mathrm{30976R}^{\mathrm{2}} +\mathrm{409600}+\mathrm{352R}^{\mathrm{3}} −\mathrm{225280R}−\mathrm{1280R}^{\mathrm{2}} =\mathrm{30720R}^{\mathrm{2}} −\mathrm{225280R}+\mathrm{409600} \\ $$$$\Leftrightarrow\:\mathrm{R}^{\mathrm{4}} +\mathrm{352R}^{\mathrm{3}} −\mathrm{1024R}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Leftrightarrow\:\mathrm{R}^{\mathrm{2}} +\mathrm{352R}−\mathrm{1024}=\mathrm{0} \\ $$$$\mathrm{therefore},\:\begin{array}{|c|}{\mathrm{R}=\mathrm{80}\sqrt{\mathrm{5}}−\mathrm{176}}\\\hline\end{array} \\ $$
Commented by Tawa11 last updated on 22/Dec/21

$$\mathrm{Great}\:\mathrm{sir} \\ $$
Commented by mr W last updated on 27/Dec/21
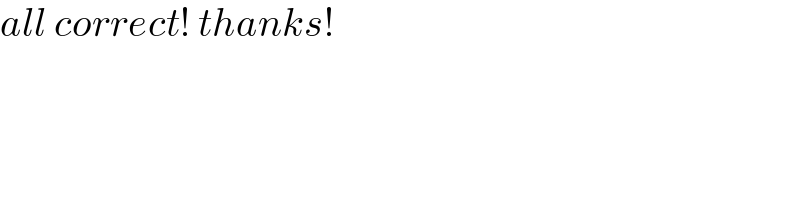
$${all}\:{correct}!\:{thanks}! \\ $$
Answered by FongXD last updated on 22/Dec/21