Question Number 161764 by Tawa11 last updated on 22/Dec/21

Commented by Tawa11 last updated on 22/Dec/21
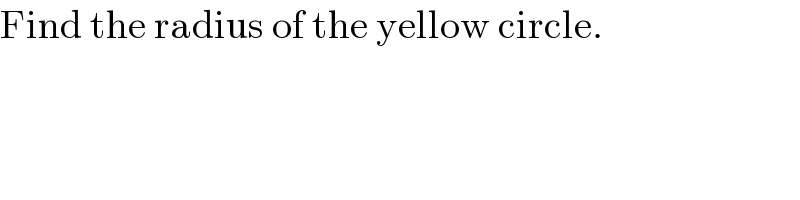
$$\mathrm{Find}\:\mathrm{the}\:\mathrm{radius}\:\mathrm{of}\:\mathrm{the}\:\mathrm{yellow}\:\mathrm{circle}. \\ $$
Commented by cortano last updated on 22/Dec/21
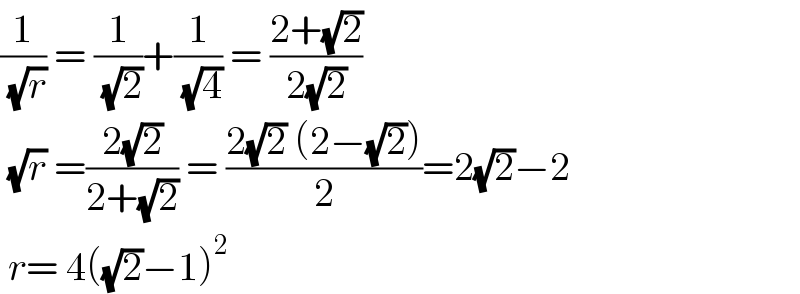
$$\frac{\mathrm{1}}{\:\sqrt{{r}}}\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{4}}}\:=\:\frac{\mathrm{2}+\sqrt{\mathrm{2}}}{\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$$\:\sqrt{{r}}\:=\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{2}+\sqrt{\mathrm{2}}}\:=\:\frac{\mathrm{2}\sqrt{\mathrm{2}}\:\left(\mathrm{2}−\sqrt{\mathrm{2}}\right)}{\mathrm{2}}=\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{2} \\ $$$$\:{r}=\:\mathrm{4}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)^{\mathrm{2}} \\ $$
Commented by Tawa11 last updated on 22/Dec/21

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by Tawa11 last updated on 22/Dec/21
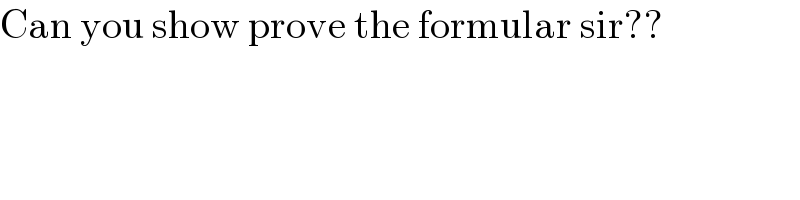
$$\mathrm{Can}\:\mathrm{you}\:\mathrm{show}\:\mathrm{prove}\:\mathrm{the}\:\mathrm{formular}\:\mathrm{sir}?? \\ $$
Commented by cortano last updated on 22/Dec/21
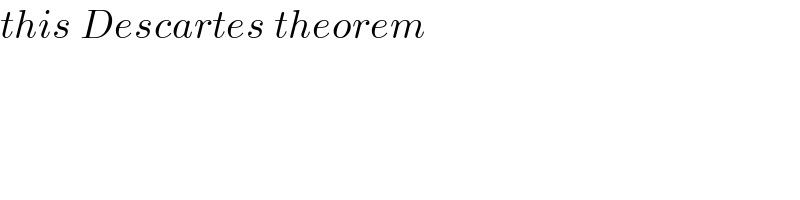
$${this}\:{Descartes}\:{theorem} \\ $$
Answered by FongXD last updated on 22/Dec/21
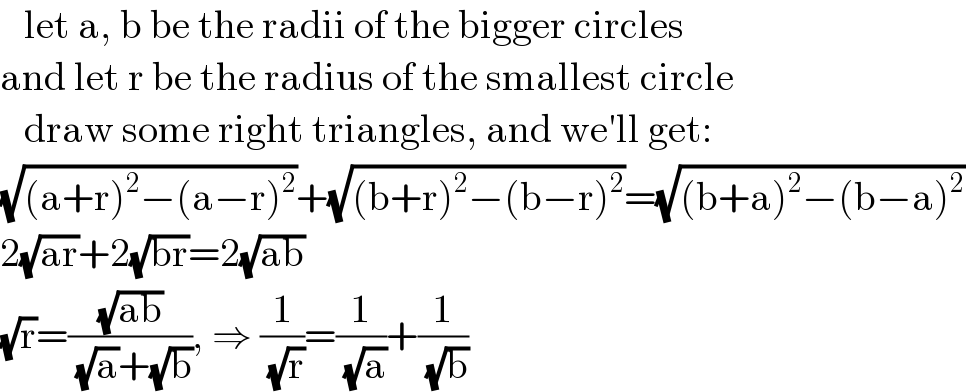
$$\:\:\:\mathrm{let}\:\mathrm{a},\:\mathrm{b}\:\mathrm{be}\:\mathrm{the}\:\mathrm{radii}\:\mathrm{of}\:\mathrm{the}\:\mathrm{bigger}\:\mathrm{circles} \\ $$$$\mathrm{and}\:\mathrm{let}\:\mathrm{r}\:\mathrm{be}\:\mathrm{the}\:\mathrm{radius}\:\mathrm{of}\:\mathrm{the}\:\mathrm{smallest}\:\mathrm{circle} \\ $$$$\:\:\:\mathrm{draw}\:\mathrm{some}\:\mathrm{right}\:\mathrm{triangles},\:\mathrm{and}\:\mathrm{we}'\mathrm{ll}\:\mathrm{get}: \\ $$$$\sqrt{\left(\mathrm{a}+\mathrm{r}\right)^{\mathrm{2}} −\left(\mathrm{a}−\mathrm{r}\right)^{\mathrm{2}} }+\sqrt{\left(\mathrm{b}+\mathrm{r}\right)^{\mathrm{2}} −\left(\mathrm{b}−\mathrm{r}\right)^{\mathrm{2}} }=\sqrt{\left(\mathrm{b}+\mathrm{a}\right)^{\mathrm{2}} −\left(\mathrm{b}−\mathrm{a}\right)^{\mathrm{2}} } \\ $$$$\mathrm{2}\sqrt{\mathrm{ar}}+\mathrm{2}\sqrt{\mathrm{br}}=\mathrm{2}\sqrt{\mathrm{ab}} \\ $$$$\sqrt{\mathrm{r}}=\frac{\sqrt{\mathrm{ab}}}{\:\sqrt{\mathrm{a}}+\sqrt{\mathrm{b}}},\:\Rightarrow\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{r}}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{a}}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{b}}} \\ $$
Commented by Tawa11 last updated on 22/Dec/21

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by mr W last updated on 22/Dec/21
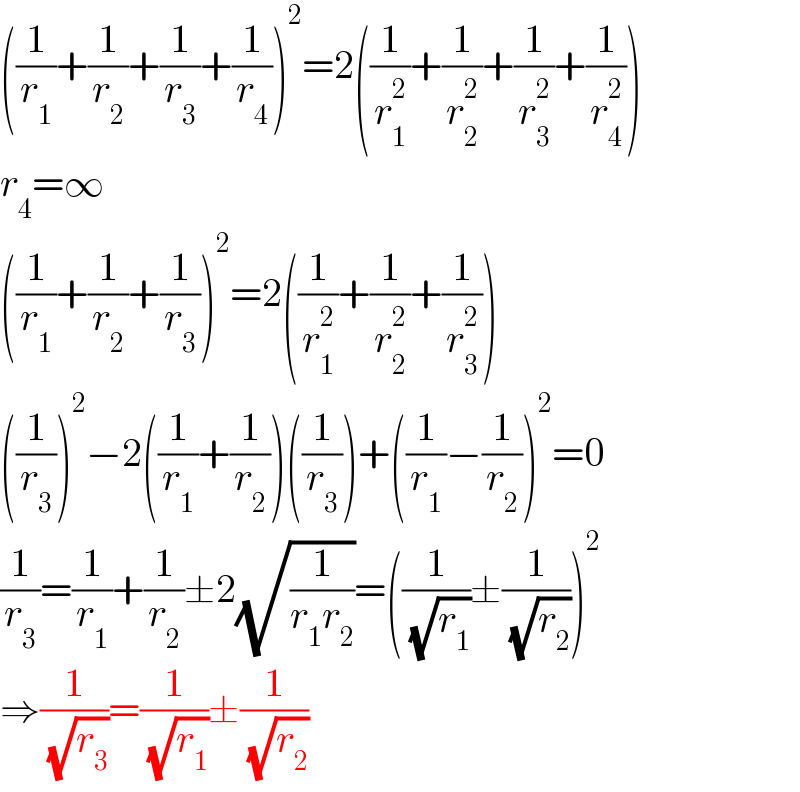
$$\left(\frac{\mathrm{1}}{{r}_{\mathrm{1}} }+\frac{\mathrm{1}}{{r}_{\mathrm{2}} }+\frac{\mathrm{1}}{{r}_{\mathrm{3}} }+\frac{\mathrm{1}}{{r}_{\mathrm{4}} }\right)^{\mathrm{2}} =\mathrm{2}\left(\frac{\mathrm{1}}{{r}_{\mathrm{1}} ^{\mathrm{2}} }+\frac{\mathrm{1}}{{r}_{\mathrm{2}} ^{\mathrm{2}} }+\frac{\mathrm{1}}{{r}_{\mathrm{3}} ^{\mathrm{2}} }+\frac{\mathrm{1}}{{r}_{\mathrm{4}} ^{\mathrm{2}} }\right) \\ $$$${r}_{\mathrm{4}} =\infty \\ $$$$\left(\frac{\mathrm{1}}{{r}_{\mathrm{1}} }+\frac{\mathrm{1}}{{r}_{\mathrm{2}} }+\frac{\mathrm{1}}{{r}_{\mathrm{3}} }\right)^{\mathrm{2}} =\mathrm{2}\left(\frac{\mathrm{1}}{{r}_{\mathrm{1}} ^{\mathrm{2}} }+\frac{\mathrm{1}}{{r}_{\mathrm{2}} ^{\mathrm{2}} }+\frac{\mathrm{1}}{{r}_{\mathrm{3}} ^{\mathrm{2}} }\right) \\ $$$$\left(\frac{\mathrm{1}}{{r}_{\mathrm{3}} }\right)^{\mathrm{2}} −\mathrm{2}\left(\frac{\mathrm{1}}{{r}_{\mathrm{1}} }+\frac{\mathrm{1}}{{r}_{\mathrm{2}} }\right)\left(\frac{\mathrm{1}}{{r}_{\mathrm{3}} }\right)+\left(\frac{\mathrm{1}}{{r}_{\mathrm{1}} }−\frac{\mathrm{1}}{{r}_{\mathrm{2}} }\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\frac{\mathrm{1}}{{r}_{\mathrm{3}} }=\frac{\mathrm{1}}{{r}_{\mathrm{1}} }+\frac{\mathrm{1}}{{r}_{\mathrm{2}} }\pm\mathrm{2}\sqrt{\frac{\mathrm{1}}{{r}_{\mathrm{1}} {r}_{\mathrm{2}} }}=\left(\frac{\mathrm{1}}{\:\sqrt{{r}_{\mathrm{1}} }}\pm\frac{\mathrm{1}}{\:\sqrt{{r}_{\mathrm{2}} }}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\:\sqrt{{r}_{\mathrm{3}} }}=\frac{\mathrm{1}}{\:\sqrt{{r}_{\mathrm{1}} }}\pm\frac{\mathrm{1}}{\:\sqrt{{r}_{\mathrm{2}} }} \\ $$
Commented by mr W last updated on 22/Dec/21

Commented by Tawa11 last updated on 22/Dec/21

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by mr W last updated on 22/Dec/21
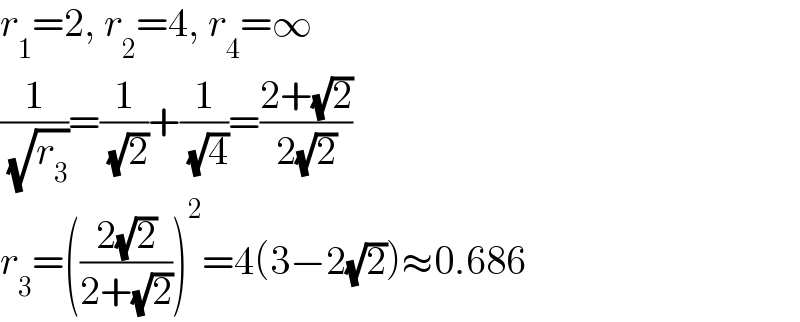
$${r}_{\mathrm{1}} =\mathrm{2},\:{r}_{\mathrm{2}} =\mathrm{4},\:{r}_{\mathrm{4}} =\infty \\ $$$$\frac{\mathrm{1}}{\:\sqrt{{r}_{\mathrm{3}} }}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{4}}}=\frac{\mathrm{2}+\sqrt{\mathrm{2}}}{\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$${r}_{\mathrm{3}} =\left(\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{2}+\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} =\mathrm{4}\left(\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}}\right)\approx\mathrm{0}.\mathrm{686} \\ $$
