Question-161811

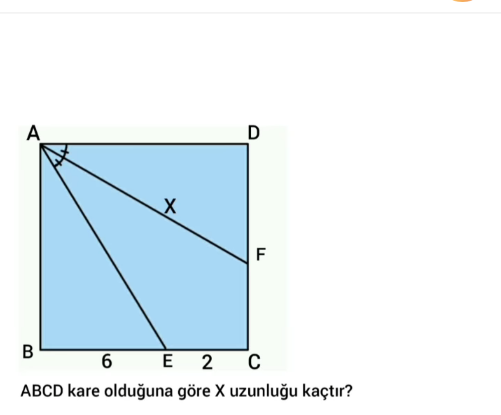
Question Number 161811 by mnjuly1970 last updated on 22/Dec/21

Answered by mnjuly1970 last updated on 22/Dec/21

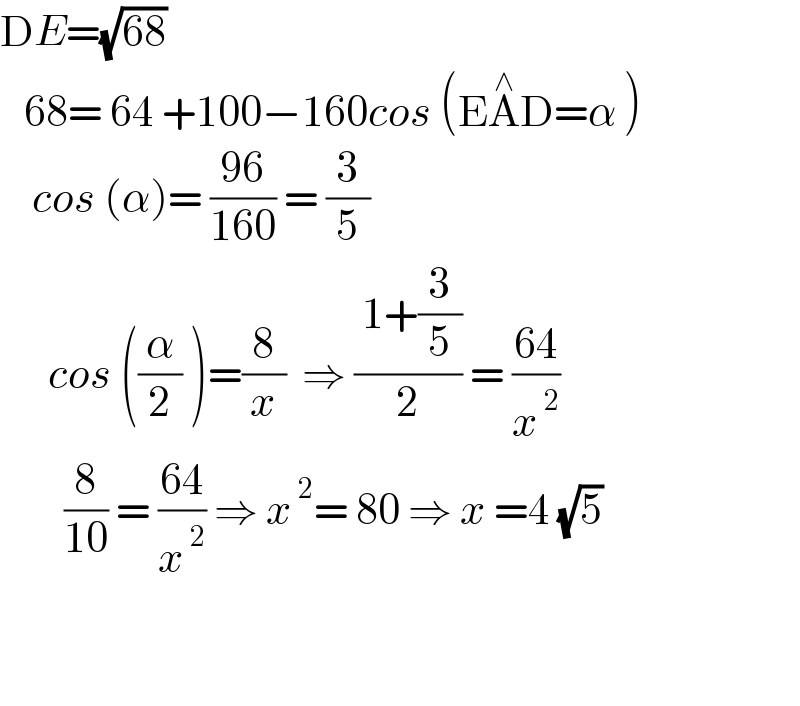
DE=(√(68)) 68= 64 +100−160cos (EA^∧ D=α ) cos (α)= ((96)/(160)) = (3/5) cos ((α/2) )=(8/x) ⇒ (( 1+(3/5))/2) = ((64)/x^( 2) ) (8/(10)) = ((64)/x^( 2) ) ⇒ x^( 2) = 80 ⇒ x =4 (√5)

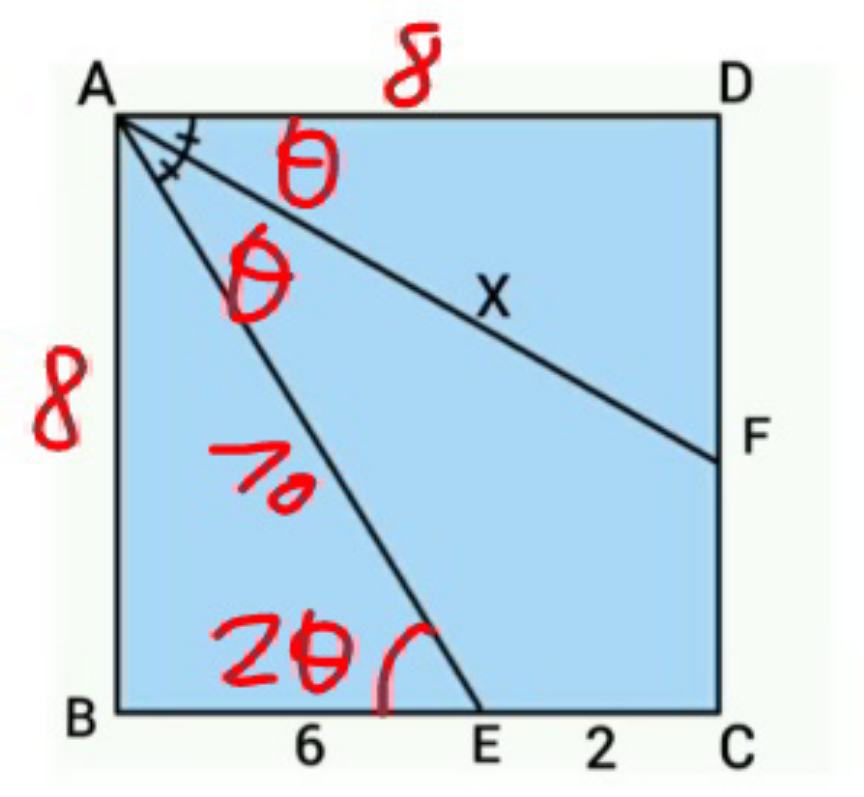
$$\mathrm{D}{E}=\sqrt{\mathrm{68}} \\ $$$$\:\:\:\mathrm{68}=\:\mathrm{64}\:+\mathrm{100}−\mathrm{160}{cos}\:\left(\mathrm{E}\overset{\wedge} {\mathrm{A}D}=\alpha\:\right) \\ $$$$\:\:\:\:{cos}\:\left(\alpha\right)=\:\frac{\mathrm{96}}{\mathrm{160}}\:=\:\frac{\mathrm{3}}{\mathrm{5}}\: \\ $$$$\:\:\:\:\:\:{cos}\:\left(\frac{\alpha}{\mathrm{2}}\:\right)=\frac{\mathrm{8}}{{x}}\:\:\Rightarrow\:\frac{\:\mathrm{1}+\frac{\mathrm{3}}{\mathrm{5}}}{\mathrm{2}}\:=\:\frac{\mathrm{64}}{{x}^{\:\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\frac{\mathrm{8}}{\mathrm{10}}\:=\:\frac{\mathrm{64}}{{x}^{\:\mathrm{2}} }\:\Rightarrow\:{x}^{\:\mathrm{2}} =\:\mathrm{80}\:\Rightarrow\:{x}\:=\mathrm{4}\:\sqrt{\mathrm{5}} \\ $$$$\:\:\: \\ $$$$\:\:\:\:\:\:\: \\ $$

Answered by Rasheed.Sindhi last updated on 22/Dec/21

AB=8 AE=(√(8^2 +6^2 )) =10 ∠BAE=θ cosθ=((AB)/(AE)) =(8/(10))=(4/5) θ=cos^(−1) ((4/5)) ∠FAD=((90−θ)/2) AD=8 cos∠FAD=cos((90−θ)/2)=((AD)/(AF))=(8/x) x=(8/(cos((90−θ)/2)))=(8/(cos(((90−cos^(−1) ((4/5)))/2)) )) x=(8/(cos(((90−36.870)/2)) ))≈8.94

$$\mathrm{AB}=\mathrm{8} \\ $$$$\mathrm{AE}=\sqrt{\mathrm{8}^{\mathrm{2}} +\mathrm{6}^{\mathrm{2}} }\:=\mathrm{10} \\ $$$$\angle\mathrm{BAE}=\theta \\ $$$$\mathrm{cos}\theta=\frac{\mathrm{AB}}{\mathrm{AE}}\:=\frac{\mathrm{8}}{\mathrm{10}}=\frac{\mathrm{4}}{\mathrm{5}} \\ $$$$\theta=\mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{4}}{\mathrm{5}}\right) \\ $$$$\angle\mathrm{FAD}=\frac{\mathrm{90}−\theta}{\mathrm{2}} \\ $$$$\mathrm{AD}=\mathrm{8} \\ $$$$\mathrm{cos}\angle\mathrm{FAD}=\mathrm{cos}\frac{\mathrm{90}−\theta}{\mathrm{2}}=\frac{\mathrm{AD}}{\mathrm{AF}}=\frac{\mathrm{8}}{\mathrm{x}}\:\: \\ $$$$\mathrm{x}=\frac{\mathrm{8}}{\mathrm{cos}\frac{\mathrm{90}−\theta}{\mathrm{2}}}=\frac{\mathrm{8}}{\mathrm{cos}\left(\frac{\mathrm{90}−\mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{4}}{\mathrm{5}}\right)}{\mathrm{2}}\right)\:} \\ $$$$\mathrm{x}=\frac{\mathrm{8}}{\mathrm{cos}\left(\frac{\mathrm{90}−\mathrm{36}.\mathrm{870}}{\mathrm{2}}\right)\:}\approx\mathrm{8}.\mathrm{94} \\ $$

Answered by mr W last updated on 22/Dec/21

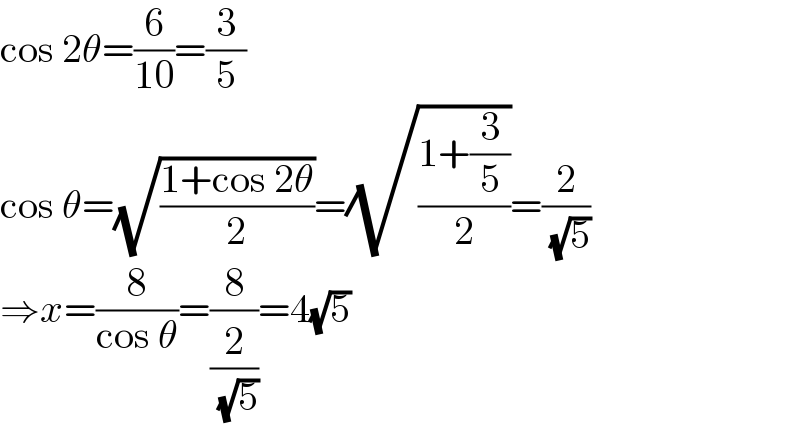
cos 2θ=(6/(10))=(3/5) cos θ=(√((1+cos 2θ)/2))=(√((1+(3/5))/2))=(2/( (√5))) ⇒x=(8/(cos θ))=(8/(2/( (√5))))=4(√5)

$$\mathrm{cos}\:\mathrm{2}\theta=\frac{\mathrm{6}}{\mathrm{10}}=\frac{\mathrm{3}}{\mathrm{5}} \\ $$$$\mathrm{cos}\:\theta=\sqrt{\frac{\mathrm{1}+\mathrm{cos}\:\mathrm{2}\theta}{\mathrm{2}}}=\sqrt{\frac{\mathrm{1}+\frac{\mathrm{3}}{\mathrm{5}}}{\mathrm{2}}}=\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}} \\ $$$$\Rightarrow{x}=\frac{\mathrm{8}}{\mathrm{cos}\:\theta}=\frac{\mathrm{8}}{\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}}=\mathrm{4}\sqrt{\mathrm{5}} \\ $$

Commented by mnjuly1970 last updated on 23/Dec/21