Question Number 161815 by HongKing last updated on 22/Dec/21
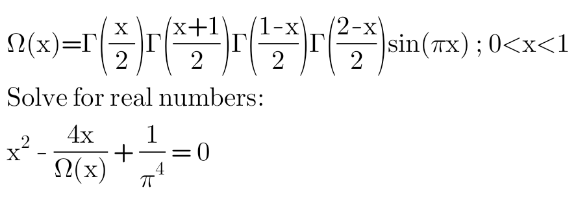
Answered by Lordose last updated on 23/Dec/21
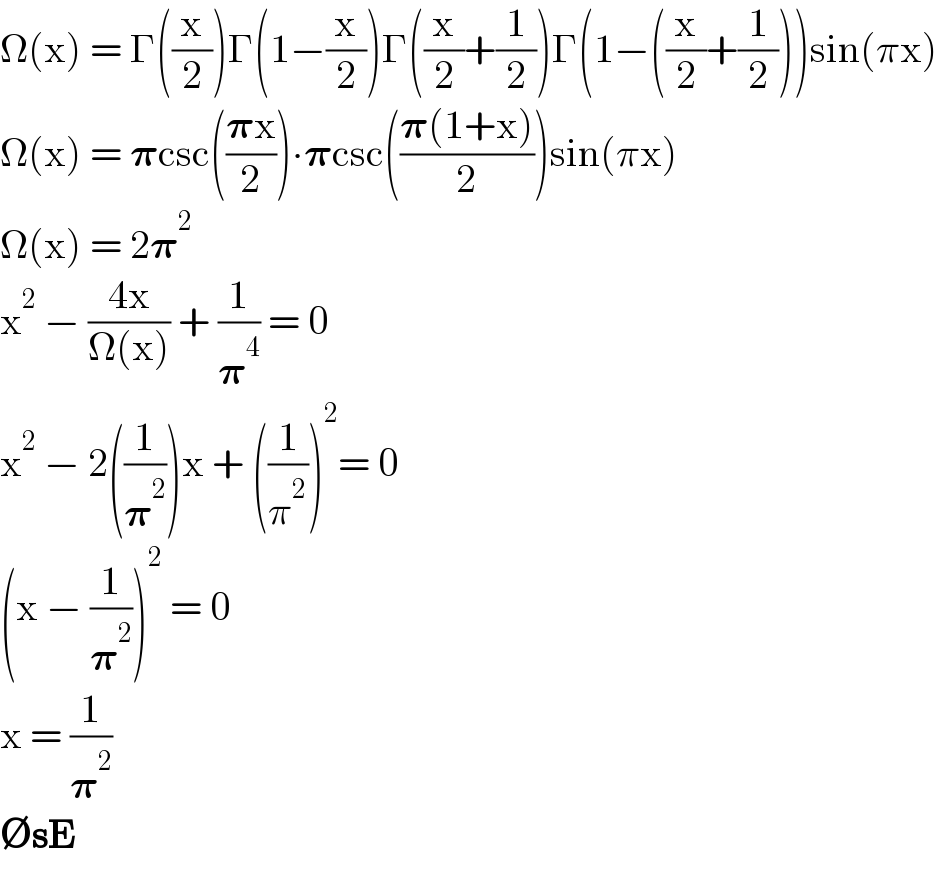
$$\Omega\left(\mathrm{x}\right)\:=\:\Gamma\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\Gamma\left(\mathrm{1}−\frac{\mathrm{x}}{\mathrm{2}}\right)\Gamma\left(\frac{\mathrm{x}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\right)\Gamma\left(\mathrm{1}−\left(\frac{\mathrm{x}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\right)\right)\mathrm{sin}\left(\pi\mathrm{x}\right) \\ $$$$\Omega\left(\mathrm{x}\right)\:=\:\boldsymbol{\pi}\mathrm{csc}\left(\frac{\boldsymbol{\pi}\mathrm{x}}{\mathrm{2}}\right)\centerdot\boldsymbol{\pi}\mathrm{csc}\left(\frac{\boldsymbol{\pi}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{2}}\right)\mathrm{sin}\left(\pi\mathrm{x}\right) \\ $$$$\Omega\left(\mathrm{x}\right)\:=\:\mathrm{2}\boldsymbol{\pi}^{\mathrm{2}} \\ $$$$\mathrm{x}^{\mathrm{2}} \:−\:\frac{\mathrm{4x}}{\Omega\left(\mathrm{x}\right)}\:+\:\frac{\mathrm{1}}{\boldsymbol{\pi}^{\mathrm{4}} }\:=\:\mathrm{0} \\ $$$$\mathrm{x}^{\mathrm{2}} \:−\:\mathrm{2}\left(\frac{\mathrm{1}}{\boldsymbol{\pi}^{\mathrm{2}} }\right)\mathrm{x}\:+\:\left(\frac{\mathrm{1}}{\pi^{\mathrm{2}} }\right)^{\mathrm{2}} =\:\mathrm{0} \\ $$$$\left(\mathrm{x}\:−\:\frac{\mathrm{1}}{\boldsymbol{\pi}^{\mathrm{2}} }\right)^{\mathrm{2}} \:=\:\mathrm{0} \\ $$$$\mathrm{x}\:=\:\frac{\mathrm{1}}{\boldsymbol{\pi}^{\mathrm{2}} } \\ $$$$\boldsymbol{\varnothing\mathrm{sE}} \\ $$
