Question Number 161991 by mkam last updated on 25/Dec/21
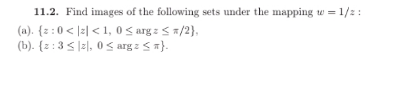
Commented by mkam last updated on 25/Dec/21

$$????? \\ $$
Answered by aleks041103 last updated on 25/Dec/21
![z=re^(it) w=(1/r)e^(−it) (a) 0<r<1 ⇒(1/r)∈(1,∞) t∈[0,π/2] ⇒−t∈[((3π)/2),2π] ⇒{z:0<∣z∣<1, 0≤arg z≤π/2}→^(w=(1/z)) {w:∣w∣>1, ((3π)/2)≤arg(w)≤2π}⊂C (b) 3≤r⇒(1/r)∈[(1/3),∞)∪{∞} t∈[0,π] ⇒−t∈[π,2π] ⇒{z:∣z∣≤3, 0≤arg z≤π}→ {w:∣w∣≥(1/3), π≤arg(w)≤2π}∪{∞}⊂(C∪{∞})](https://www.tinkutara.com/question/Q162011.png)
$${z}={re}^{{it}} \\ $$$${w}=\frac{\mathrm{1}}{{r}}{e}^{−{it}} \\ $$$$\left({a}\right) \\ $$$$\mathrm{0}<{r}<\mathrm{1} \\ $$$$\Rightarrow\frac{\mathrm{1}}{{r}}\in\left(\mathrm{1},\infty\right) \\ $$$${t}\in\left[\mathrm{0},\pi/\mathrm{2}\right] \\ $$$$\Rightarrow−{t}\in\left[\frac{\mathrm{3}\pi}{\mathrm{2}},\mathrm{2}\pi\right] \\ $$$$\Rightarrow\left\{{z}:\mathrm{0}<\mid{z}\mid<\mathrm{1},\:\mathrm{0}\leq{arg}\:{z}\leq\pi/\mathrm{2}\right\}\overset{{w}=\frac{\mathrm{1}}{{z}}} {\rightarrow}\:\:\left\{{w}:\mid{w}\mid>\mathrm{1},\:\frac{\mathrm{3}\pi}{\mathrm{2}}\leq{arg}\left({w}\right)\leq\mathrm{2}\pi\right\}\subset\mathbb{C} \\ $$$$\left({b}\right) \\ $$$$\mathrm{3}\leqslant{r}\Rightarrow\frac{\mathrm{1}}{{r}}\in\left[\frac{\mathrm{1}}{\mathrm{3}},\infty\right)\cup\left\{\infty\right\} \\ $$$${t}\in\left[\mathrm{0},\pi\right] \\ $$$$\Rightarrow−{t}\in\left[\pi,\mathrm{2}\pi\right] \\ $$$$\Rightarrow\left\{{z}:\mid{z}\mid\leqslant\mathrm{3},\:\mathrm{0}\leq{arg}\:{z}\leq\pi\right\}\rightarrow\:\:\left\{{w}:\mid{w}\mid\geqslant\frac{\mathrm{1}}{\mathrm{3}},\:\pi\leq{arg}\left({w}\right)\leq\mathrm{2}\pi\right\}\cup\left\{\infty\right\}\subset\left(\mathbb{C}\cup\left\{\infty\right\}\right) \\ $$
