Question Number 162054 by amin96 last updated on 25/Dec/21

Answered by aleks041103 last updated on 25/Dec/21
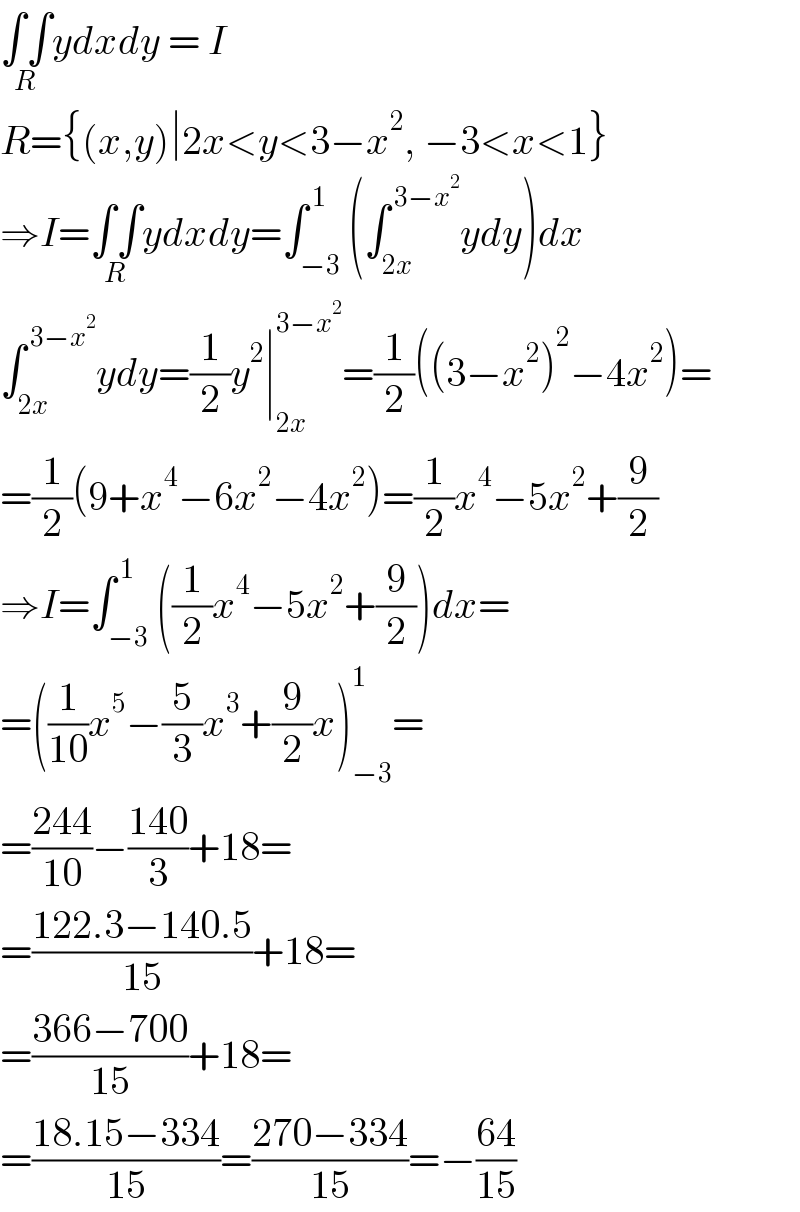
$$\underset{{R}} {\int\int}{ydxdy}\:=\:{I} \\ $$$${R}=\left\{\left({x},{y}\right)\mid\mathrm{2}{x}<{y}<\mathrm{3}−{x}^{\mathrm{2}} ,\:−\mathrm{3}<{x}<\mathrm{1}\right\} \\ $$$$\Rightarrow{I}=\underset{{R}} {\int\int}{ydxdy}=\int_{−\mathrm{3}} ^{\:\mathrm{1}} \left(\int_{\mathrm{2}{x}} ^{\:\mathrm{3}−{x}^{\mathrm{2}} } {ydy}\right){dx} \\ $$$$\int_{\mathrm{2}{x}} ^{\:\mathrm{3}−{x}^{\mathrm{2}} } {ydy}=\frac{\mathrm{1}}{\mathrm{2}}{y}^{\mathrm{2}} \mid_{\mathrm{2}{x}} ^{\mathrm{3}−{x}^{\mathrm{2}} } =\frac{\mathrm{1}}{\mathrm{2}}\left(\left(\mathrm{3}−{x}^{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{4}{x}^{\mathrm{2}} \right)= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{9}+{x}^{\mathrm{4}} −\mathrm{6}{x}^{\mathrm{2}} −\mathrm{4}{x}^{\mathrm{2}} \right)=\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{4}} −\mathrm{5}{x}^{\mathrm{2}} +\frac{\mathrm{9}}{\mathrm{2}} \\ $$$$\Rightarrow{I}=\int_{−\mathrm{3}} ^{\:\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{4}} −\mathrm{5}{x}^{\mathrm{2}} +\frac{\mathrm{9}}{\mathrm{2}}\right){dx}= \\ $$$$=\left(\frac{\mathrm{1}}{\mathrm{10}}{x}^{\mathrm{5}} −\frac{\mathrm{5}}{\mathrm{3}}{x}^{\mathrm{3}} +\frac{\mathrm{9}}{\mathrm{2}}{x}\right)_{−\mathrm{3}} ^{\mathrm{1}} = \\ $$$$=\frac{\mathrm{244}}{\mathrm{10}}−\frac{\mathrm{140}}{\mathrm{3}}+\mathrm{18}= \\ $$$$=\frac{\mathrm{122}.\mathrm{3}−\mathrm{140}.\mathrm{5}}{\mathrm{15}}+\mathrm{18}= \\ $$$$=\frac{\mathrm{366}−\mathrm{700}}{\mathrm{15}}+\mathrm{18}= \\ $$$$=\frac{\mathrm{18}.\mathrm{15}−\mathrm{334}}{\mathrm{15}}=\frac{\mathrm{270}−\mathrm{334}}{\mathrm{15}}=−\frac{\mathrm{64}}{\mathrm{15}} \\ $$
