Question-162068

Question Number 162068 by HongKing last updated on 25/Dec/21

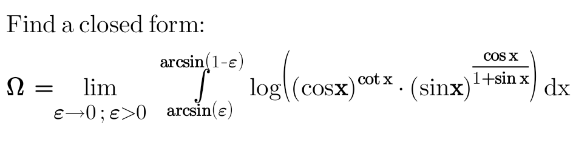
Answered by Lordose last updated on 26/Dec/21

Ω = lim_(ε→0) ∫_(sin^(−1) (ε)) ^( sin^(−1) (1−ε)) log((cos(x))^(cot(x)) ∙(sin(x))^((cos(x))/(1+sin(x))) )dx Ω = ∫_0 ^( (𝛑/2)) cot(x)log(cos(x))dx + ∫_0 ^(𝛑/2) ((cos(x))/(1+sin(x)))log(sin(x))dx Ω = A + B A =^(u=cos(x)) ∫_0 ^( 1) (u/( 1−u^2 ))log(u)du = Σ_(n=0) ^∞ ∫_0 ^( 1) u^(2n+1) log(u)du A =^(IBP) −(1/2)Σ_(n=0) ^∞ (1/(n+1))∫_0 ^( 1) u^(2n+1) du = −(1/4)Σ_(n=0) ^∞ (1/((n+1)^2 )) A = −(1/4)𝛇(2) = −(𝛑^2 /(24)) B =^(u=sin(x)) ∫_0 ^( 1) ((log(u))/(1+u))du = Li_2 (−1) = −(𝛑^2 /(12)) Ω = A + B 𝛀 = −(𝛑^2 /8) ∅sE

$$ \\ $$$$\Omega\:=\:\underset{\epsilon\rightarrow\mathrm{0}} {\mathrm{lim}}\int_{\mathrm{sin}^{−\mathrm{1}} \left(\epsilon\right)} ^{\:\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{1}−\epsilon\right)} \mathrm{log}\left(\left(\mathrm{cos}\left(\mathrm{x}\right)\right)^{\mathrm{cot}\left(\mathrm{x}\right)} \centerdot\left(\mathrm{sin}\left(\mathrm{x}\right)\right)^{\frac{\mathrm{cos}\left(\mathrm{x}\right)}{\mathrm{1}+\mathrm{sin}\left(\mathrm{x}\right)}} \right)\mathrm{dx}\:\: \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\:\frac{\boldsymbol{\pi}}{\mathrm{2}}} \mathrm{cot}\left(\mathrm{x}\right)\mathrm{log}\left(\mathrm{cos}\left(\mathrm{x}\right)\right)\mathrm{dx}\:+\:\int_{\mathrm{0}} ^{\frac{\boldsymbol{\pi}}{\mathrm{2}}} \frac{\mathrm{cos}\left(\mathrm{x}\right)}{\mathrm{1}+\mathrm{sin}\left(\mathrm{x}\right)}\mathrm{log}\left(\mathrm{sin}\left(\mathrm{x}\right)\right)\mathrm{dx}\:\:\: \\ $$$$\Omega\:=\:\mathrm{A}\:+\:\mathrm{B} \\ $$$$\mathrm{A}\:\overset{\mathrm{u}=\mathrm{cos}\left(\mathrm{x}\right)} {=}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{u}}{\:\mathrm{1}−\mathrm{u}^{\mathrm{2}} }\mathrm{log}\left(\mathrm{u}\right)\mathrm{du}\:=\:\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{\:\mathrm{1}} \mathrm{u}^{\mathrm{2n}+\mathrm{1}} \mathrm{log}\left(\mathrm{u}\right)\mathrm{du} \\ $$$$\mathrm{A}\:\overset{\boldsymbol{\mathrm{IBP}}} {=}\:−\frac{\mathrm{1}}{\mathrm{2}}\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}\int_{\mathrm{0}} ^{\:\mathrm{1}} \mathrm{u}^{\mathrm{2n}+\mathrm{1}} \mathrm{du}\:=\:−\frac{\mathrm{1}}{\mathrm{4}}\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\mathrm{A}\:=\:−\frac{\mathrm{1}}{\mathrm{4}}\boldsymbol{\zeta}\left(\mathrm{2}\right)\:=\:−\frac{\boldsymbol{\pi}^{\mathrm{2}} }{\mathrm{24}} \\ $$$$\mathrm{B}\:\overset{\mathrm{u}=\mathrm{sin}\left(\mathrm{x}\right)} {=}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{log}\left(\mathrm{u}\right)}{\mathrm{1}+\mathrm{u}}\mathrm{du}\:=\:\boldsymbol{\mathrm{Li}}_{\mathrm{2}} \left(−\mathrm{1}\right)\:=\:−\frac{\boldsymbol{\pi}^{\mathrm{2}} }{\mathrm{12}} \\ $$$$\Omega\:=\:\mathrm{A}\:+\:\mathrm{B} \\ $$$$\boldsymbol{\Omega}\:=\:−\frac{\boldsymbol{\pi}^{\mathrm{2}} }{\mathrm{8}} \\ $$$$\boldsymbol{\varnothing\mathrm{sE}} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply