Question Number 162138 by LEKOUMA last updated on 27/Dec/21
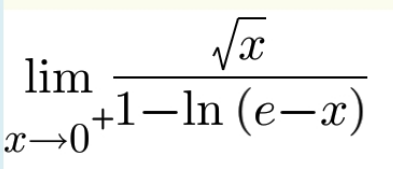
Answered by Ar Brandon last updated on 27/Dec/21
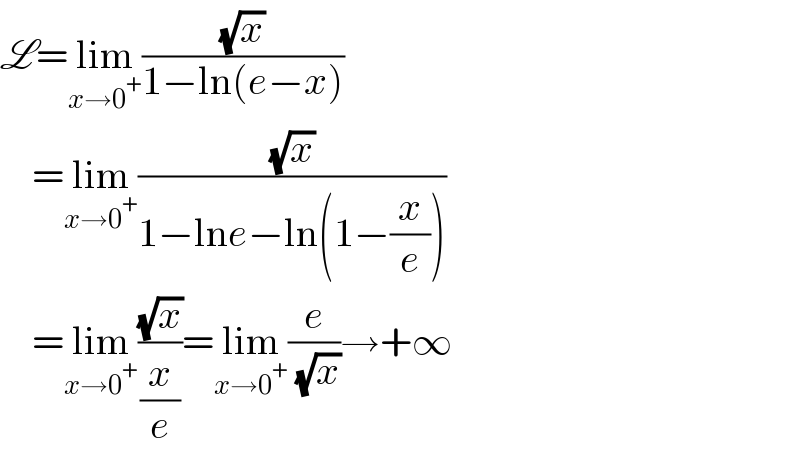
$$\mathscr{L}=\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\frac{\sqrt{{x}}}{\mathrm{1}−\mathrm{ln}\left({e}−{x}\right)} \\ $$$$\:\:\:\:=\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\frac{\sqrt{{x}}}{\mathrm{1}−\mathrm{ln}{e}−\mathrm{ln}\left(\mathrm{1}−\frac{{x}}{{e}}\right)} \\ $$$$\:\:\:\:=\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\frac{\sqrt{{x}}}{\frac{{x}}{{e}}}=\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\frac{{e}}{\:\sqrt{{x}}}\rightarrow+\infty \\ $$
