Menu Close

Question-162139

Tinku Tara 0 Comments
Pin




Question Number 162139 by LEKOUMA last updated on 27/Dec/21
Answered by alephzero last updated on 27/Dec/21
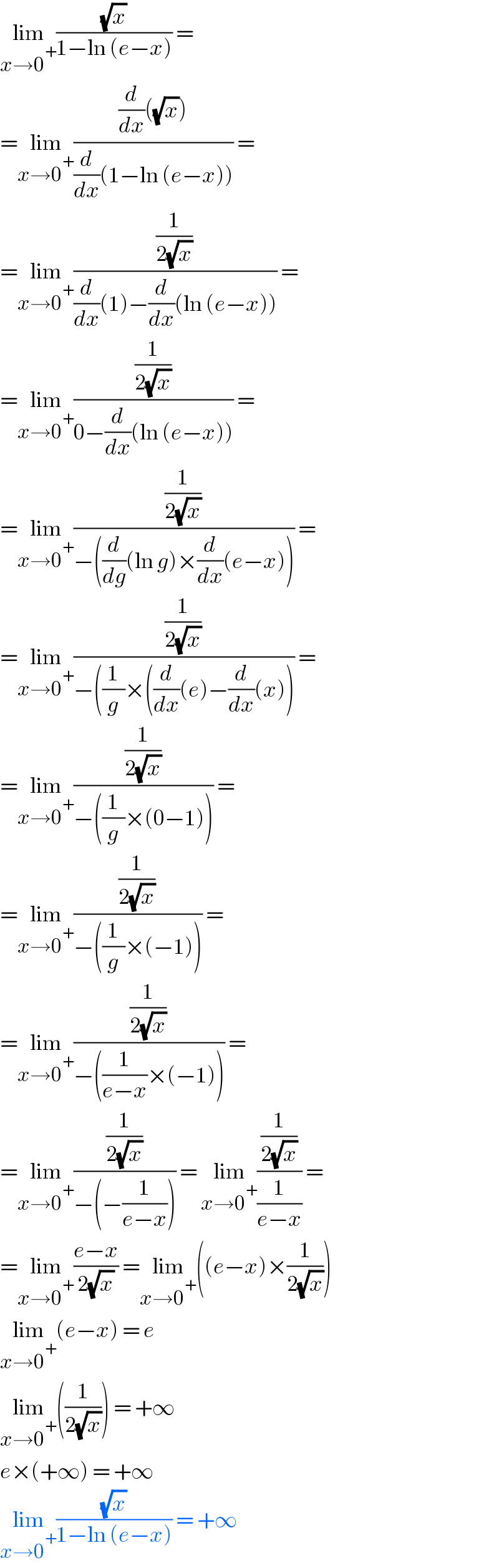
lim_(x→0^+ ) ((√x)/(1−ln (e−x))) = =lim_(x→0^+ ) (((d/dx)((√x)))/((d/dx)(1−ln (e−x)))) = =lim_(x→0^+ ) ((1/(2(√x)))/((d/dx)(1)−(d/dx)(ln (e−x)))) = =lim_(x→0^+ ) ((1/(2(√x)))/(0−(d/dx)(ln (e−x)))) = =lim_(x→0^+ ) ((1/(2(√x)))/(−((d/dg)(ln g)×(d/dx)(e−x)))) = =lim_(x→0^+ ) ((1/(2(√x)))/(−((1/g)×((d/dx)(e)−(d/dx)(x)))) = =lim_(x→0^+ ) ((1/(2(√x)))/(−((1/g)×(0−1)))) = =lim_(x→0^+ ) ((1/(2(√x)))/(−((1/g)×(−1)))) = =lim_(x→0^+ ) ((1/(2(√x)))/(−((1/(e−x))×(−1)))) = =lim_(x→0^+ ) ((1/(2(√x)))/(−(−(1/(e−x))))) = lim_(x→0^+ ) ((1/(2(√x)))/(1/(e−x))) = =lim_(x→0^+ ) ((e−x)/(2(√x))) =lim_(x→0^+ ) ((e−x)×(1/(2(√x)))) lim_(x→0^+ ) (e−x) = e lim_(x→0^+ ) ((1/(2(√x)))) = +∞ e×(+∞) = +∞ lim_(x→0^+ ) ((√x)/(1−ln (e−x))) = +∞
$$\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\frac{\sqrt{{x}}}{\mathrm{1}−\mathrm{ln}\:\left({e}−{x}\right)}\:=\: \\ $$$$=\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\frac{\frac{{d}}{{dx}}\left(\sqrt{{x}}\right)}{\frac{{d}}{{dx}}\left(\mathrm{1}−\mathrm{ln}\:\left({e}−{x}\right)\right)}\:=\: \\ $$$$=\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\frac{\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}}}}{\frac{{d}}{{dx}}\left(\mathrm{1}\right)−\frac{{d}}{{dx}}\left(\mathrm{ln}\:\left({e}−{x}\right)\right)}\:= \\ $$$$=\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\frac{\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}}}}{\mathrm{0}−\frac{{d}}{{dx}}\left(\mathrm{ln}\:\left({e}−{x}\right)\right)}\:=\: \\ $$$$=\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\frac{\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}}}}{−\left(\frac{{d}}{{dg}}\left(\mathrm{ln}\:{g}\right)×\frac{{d}}{{dx}}\left({e}−{x}\right)\right)}\:= \\ $$$$=\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\frac{\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}}}}{−\left(\frac{\mathrm{1}}{{g}}×\left(\frac{{d}}{{dx}}\left({e}\right)−\frac{{d}}{{dx}}\left({x}\right)\right)\right.}\:= \\ $$$$=\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\frac{\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}}}}{−\left(\frac{\mathrm{1}}{{g}}×\left(\mathrm{0}−\mathrm{1}\right)\right)}\:=\: \\ $$$$=\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\frac{\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}}}}{−\left(\frac{\mathrm{1}}{{g}}×\left(−\mathrm{1}\right)\right)}\:= \\ $$$$=\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\frac{\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}}}}{−\left(\frac{\mathrm{1}}{{e}−{x}}×\left(−\mathrm{1}\right)\right)}\:= \\ $$$$=\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\frac{\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}}}}{−\left(−\frac{\mathrm{1}}{{e}−{x}}\right)}\:=\:\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\frac{\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}}}}{\frac{\mathrm{1}}{{e}−{x}}}\:= \\ $$$$=\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\frac{{e}−{x}}{\mathrm{2}\sqrt{{x}}}\:=\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\left(\left({e}−{x}\right)×\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}}}\right) \\ $$$$\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\left({e}−{x}\right)\:=\:{e} \\ $$$$\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\left(\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}}}\right)\:=\:+\infty \\ $$$${e}×\left(+\infty\right)\:=\:+\infty \\ $$$$\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\frac{\sqrt{{x}}}{\mathrm{1}−\mathrm{ln}\:\left({e}−{x}\right)}\:=\:+\infty \\ $$
Answered by mathmax by abdo last updated on 27/Dec/21
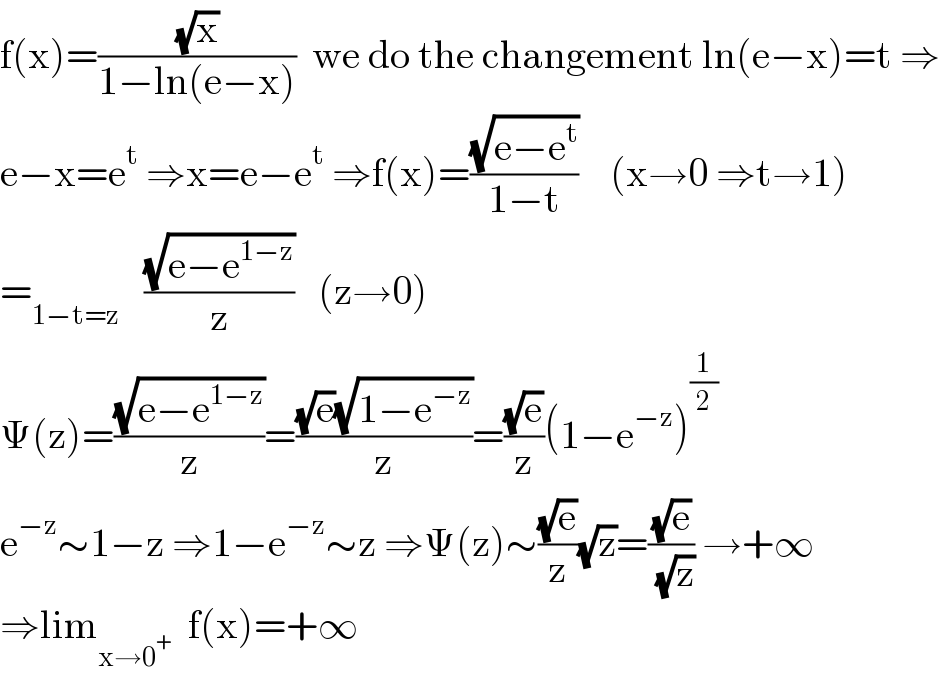
f(x)=((√x)/(1−ln(e−x))) we do the changement ln(e−x)=t ⇒ e−x=e^t ⇒x=e−e^t ⇒f(x)=((√(e−e^t ))/(1−t)) (x→0 ⇒t→1) =_(1−t=z) ((√(e−e^(1−z) ))/z) (z→0) Ψ(z)=((√(e−e^(1−z) ))/z)=(((√e)(√(1−e^(−z) )))/z)=((√e)/z)(1−e^(−z) )^(1/2) e^(−z) ∼1−z ⇒1−e^(−z) ∼z ⇒Ψ(z)∼((√e)/z)(√z)=((√e)/( (√z))) →+∞ ⇒lim_(x→0^+ ) f(x)=+∞
$$\mathrm{f}\left(\mathrm{x}\right)=\frac{\sqrt{\mathrm{x}}}{\mathrm{1}−\mathrm{ln}\left(\mathrm{e}−\mathrm{x}\right)}\:\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\mathrm{ln}\left(\mathrm{e}−\mathrm{x}\right)=\mathrm{t}\:\Rightarrow \\ $$$$\mathrm{e}−\mathrm{x}=\mathrm{e}^{\mathrm{t}} \:\Rightarrow\mathrm{x}=\mathrm{e}−\mathrm{e}^{\mathrm{t}} \:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\frac{\sqrt{\mathrm{e}−\mathrm{e}^{\mathrm{t}} }}{\mathrm{1}−\mathrm{t}}\:\:\:\:\left(\mathrm{x}\rightarrow\mathrm{0}\:\Rightarrow\mathrm{t}\rightarrow\mathrm{1}\right) \\ $$$$=_{\mathrm{1}−\mathrm{t}=\mathrm{z}} \:\:\:\frac{\sqrt{\mathrm{e}−\mathrm{e}^{\mathrm{1}−\mathrm{z}} }}{\mathrm{z}}\:\:\:\left(\mathrm{z}\rightarrow\mathrm{0}\right) \\ $$$$\Psi\left(\mathrm{z}\right)=\frac{\sqrt{\mathrm{e}−\mathrm{e}^{\mathrm{1}−\mathrm{z}} }}{\mathrm{z}}=\frac{\sqrt{\mathrm{e}}\sqrt{\mathrm{1}−\mathrm{e}^{−\mathrm{z}} }}{\mathrm{z}}=\frac{\sqrt{\mathrm{e}}}{\mathrm{z}}\left(\mathrm{1}−\mathrm{e}^{−\mathrm{z}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\mathrm{e}^{−\mathrm{z}} \sim\mathrm{1}−\mathrm{z}\:\Rightarrow\mathrm{1}−\mathrm{e}^{−\mathrm{z}} \sim\mathrm{z}\:\Rightarrow\Psi\left(\mathrm{z}\right)\sim\frac{\sqrt{\mathrm{e}}}{\mathrm{z}}\sqrt{\mathrm{z}}=\frac{\sqrt{\mathrm{e}}}{\:\sqrt{\mathrm{z}}}\:\rightarrow+\infty \\ $$$$\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}^{+} } \:\:\mathrm{f}\left(\mathrm{x}\right)=+\infty \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *