Question Number 162151 by Tawa11 last updated on 27/Dec/21
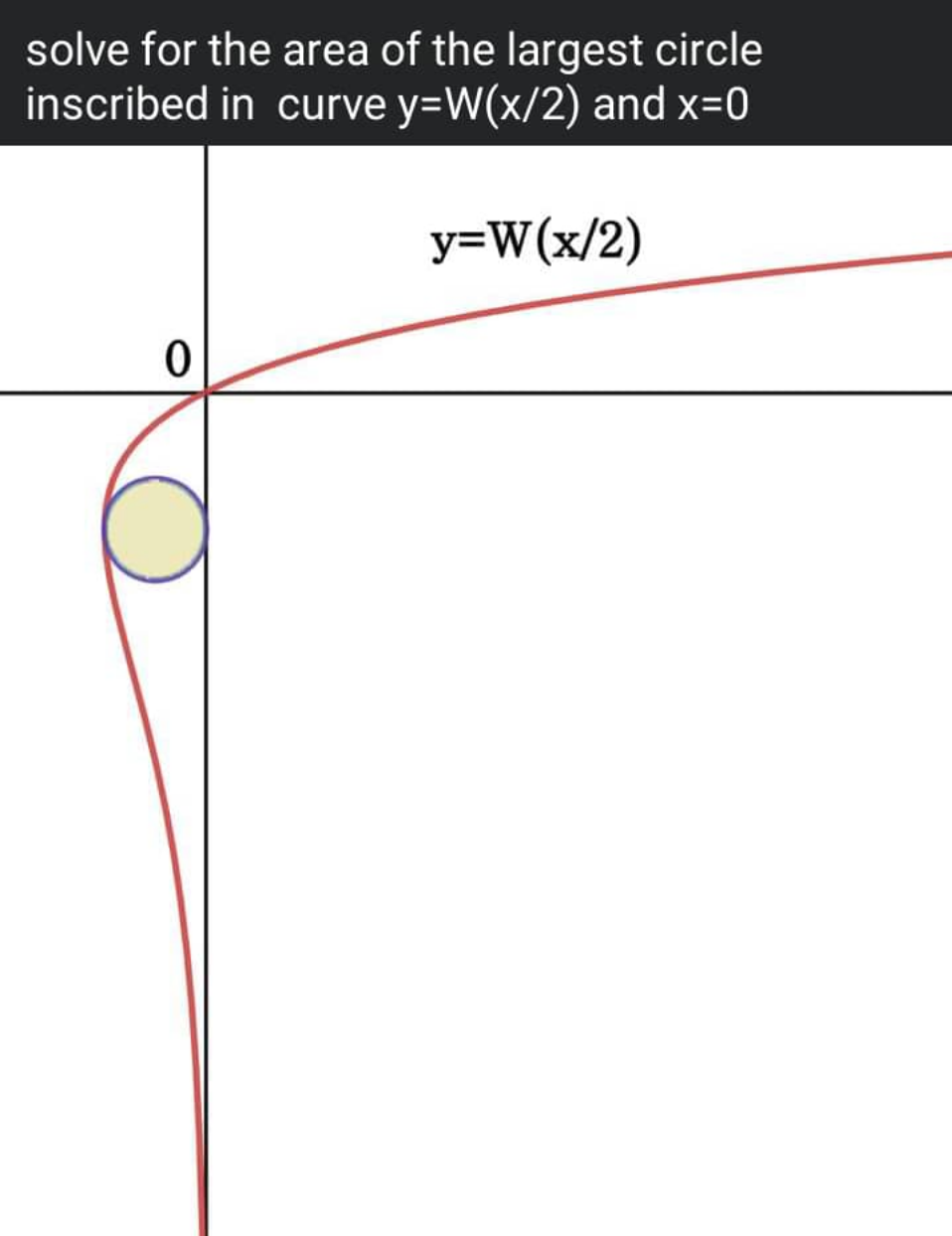
Answered by mr W last updated on 27/Dec/21
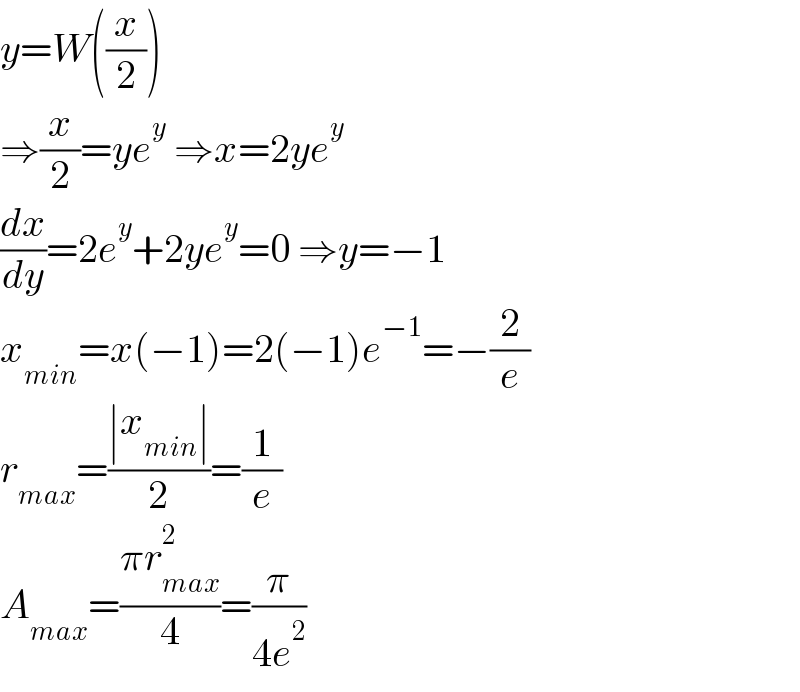
$${y}={W}\left(\frac{{x}}{\mathrm{2}}\right) \\ $$$$\Rightarrow\frac{{x}}{\mathrm{2}}={ye}^{{y}} \:\Rightarrow{x}=\mathrm{2}{ye}^{{y}} \\ $$$$\frac{{dx}}{{dy}}=\mathrm{2}{e}^{{y}} +\mathrm{2}{ye}^{{y}} =\mathrm{0}\:\Rightarrow{y}=−\mathrm{1} \\ $$$${x}_{{min}} ={x}\left(−\mathrm{1}\right)=\mathrm{2}\left(−\mathrm{1}\right){e}^{−\mathrm{1}} =−\frac{\mathrm{2}}{{e}} \\ $$$${r}_{{max}} =\frac{\mid{x}_{{min}} \mid}{\mathrm{2}}=\frac{\mathrm{1}}{{e}} \\ $$$${A}_{{max}} =\frac{\pi{r}_{{max}} ^{\mathrm{2}} }{\mathrm{4}}=\frac{\pi}{\mathrm{4}{e}^{\mathrm{2}} } \\ $$
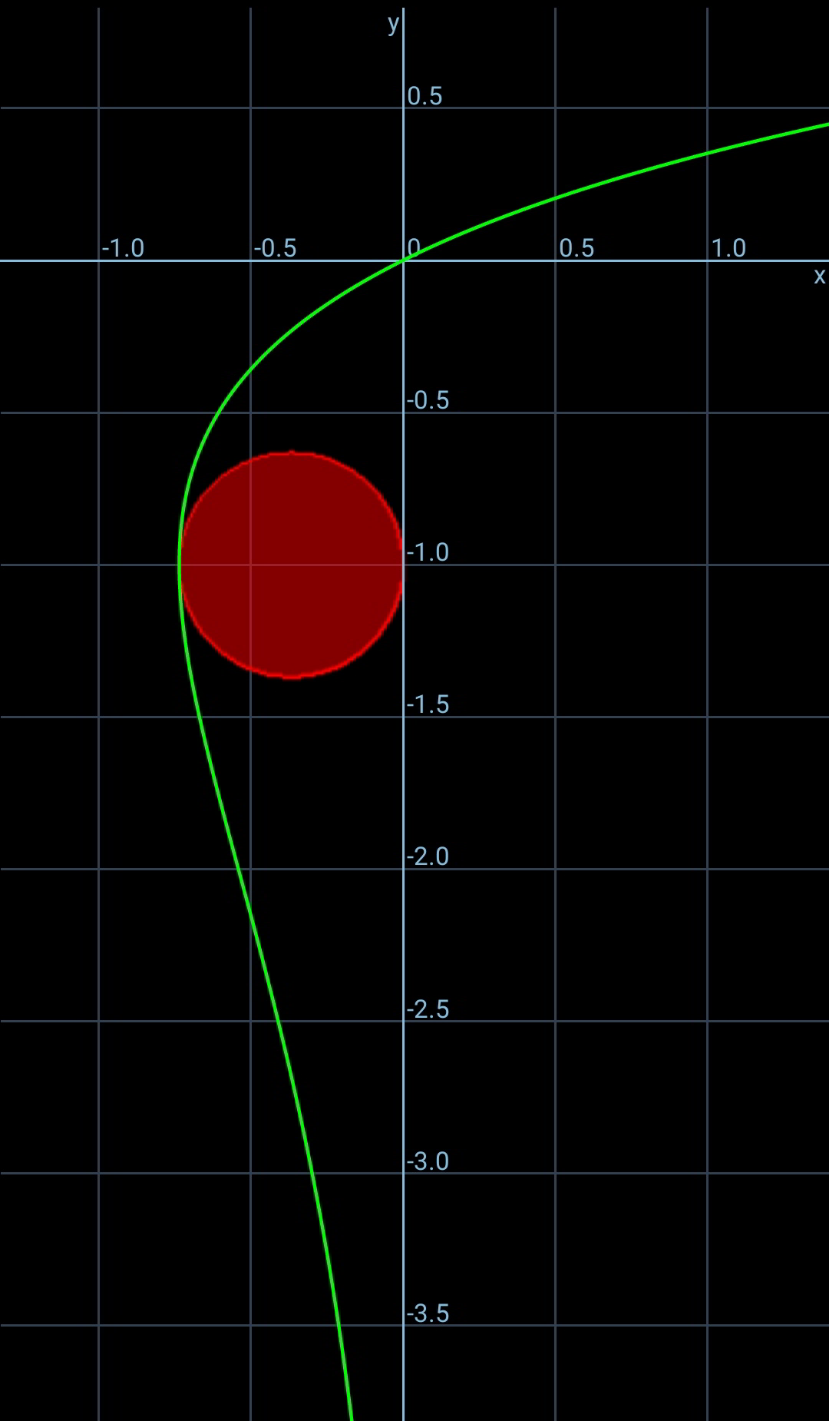
Commented by mr W last updated on 27/Dec/21
Commented by Tawa11 last updated on 27/Dec/21
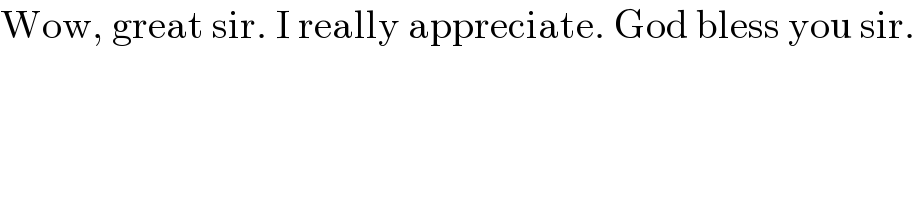
$$\mathrm{Wow},\:\mathrm{great}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{really}\:\mathrm{appreciate}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by Tawa11 last updated on 27/Dec/21
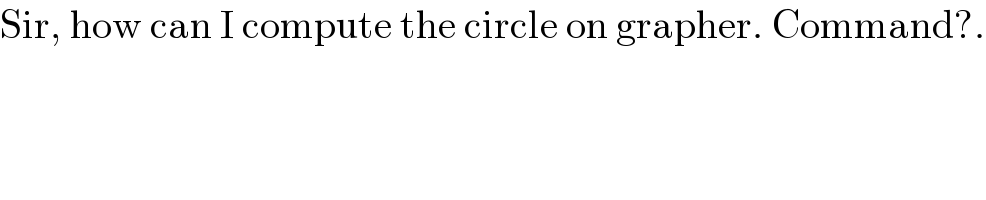
$$\mathrm{Sir},\:\mathrm{how}\:\mathrm{can}\:\mathrm{I}\:\mathrm{compute}\:\mathrm{the}\:\mathrm{circle}\:\mathrm{on}\:\mathrm{grapher}.\:\mathrm{Command}?. \\ $$
Commented by mr W last updated on 27/Dec/21
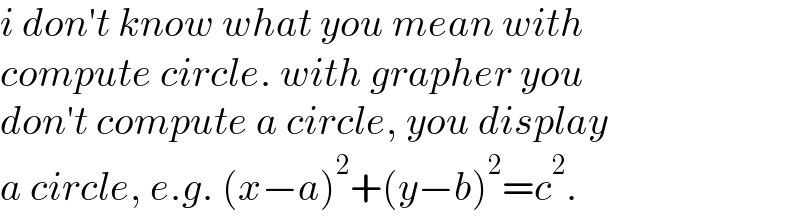
$${i}\:{don}'{t}\:{know}\:{what}\:{you}\:{mean}\:{with}\: \\ $$$${compute}\:{circle}.\:{with}\:{grapher}\:{you} \\ $$$${don}'{t}\:{compute}\:{a}\:{circle},\:{you}\:{display} \\ $$$${a}\:{circle},\:{e}.{g}.\:\left({x}−{a}\right)^{\mathrm{2}} +\left({y}−{b}\right)^{\mathrm{2}} ={c}^{\mathrm{2}} . \\ $$
Commented by aleks041103 last updated on 28/Dec/21
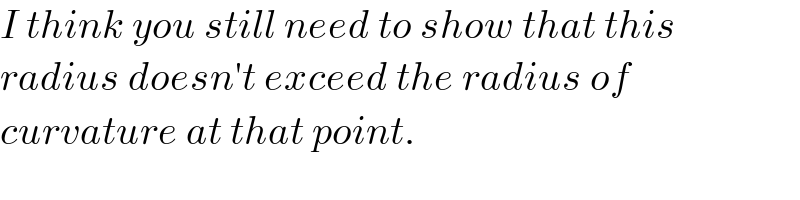
$${I}\:{think}\:{you}\:{still}\:{need}\:{to}\:{show}\:{that}\:{this} \\ $$$${radius}\:{doesn}'{t}\:{exceed}\:{the}\:{radius}\:{of}\: \\ $$$${curvature}\:{at}\:{that}\:{point}. \\ $$
Commented by mr W last updated on 28/Dec/21

$${yes}.\:{i}\:{knew}.\:{i}\:{checked}\:{that}\:{also}.\:{but} \\ $$$${since}\:{i}'{m}\:{not}\:{doing}\:{a}\:{school}\: \\ $$$${examination}\:{here},\:{so}\:{i}\:{don}'{t}\:{write} \\ $$$${everything}\:{down}\:{which}\:{i}\:{think}\:{is} \\ $$$${clear}\:{or}\:{obvious}.\:{anyway},\:{thanks}\:{for} \\ $$$${your}\:{hint}! \\ $$
Commented by aleks041103 last updated on 28/Dec/21

$${I}\:{undrstand}.\:{I}\:{didn}'{t}\:{want}\:{to}\:{offend} \\ $$$${you}!\:{I}'{ve}\:{allways}\:{tried}\:{to}\:{write}\:{down} \\ $$$${everything},\:{but}\:{you}\:{showed}\:{me}\:{that} \\ $$$${this}\:{isn}'{t}\:{neccessary}.\:{Thanks}! \\ $$
Commented by mr W last updated on 28/Dec/21

$${you}\:{decide}\:{what}\:{you}\:{want}\:{to}\:{do}, \\ $$$${nobody}\:{else}.\:{i}\:{don}'{t}\:{want}\:{to}\:{show}\: \\ $$$${anybody}\:{what}\:{is}\:{necessary}\:{to}\:{him}, \\ $$$${i}\:{just}\:{do}\:{what}\:{i}\:{think}\:{is}\:{necessary}\:{to} \\ $$$${myself}. \\ $$
