Question Number 162183 by Tawa11 last updated on 27/Dec/21

Answered by mr W last updated on 27/Dec/21
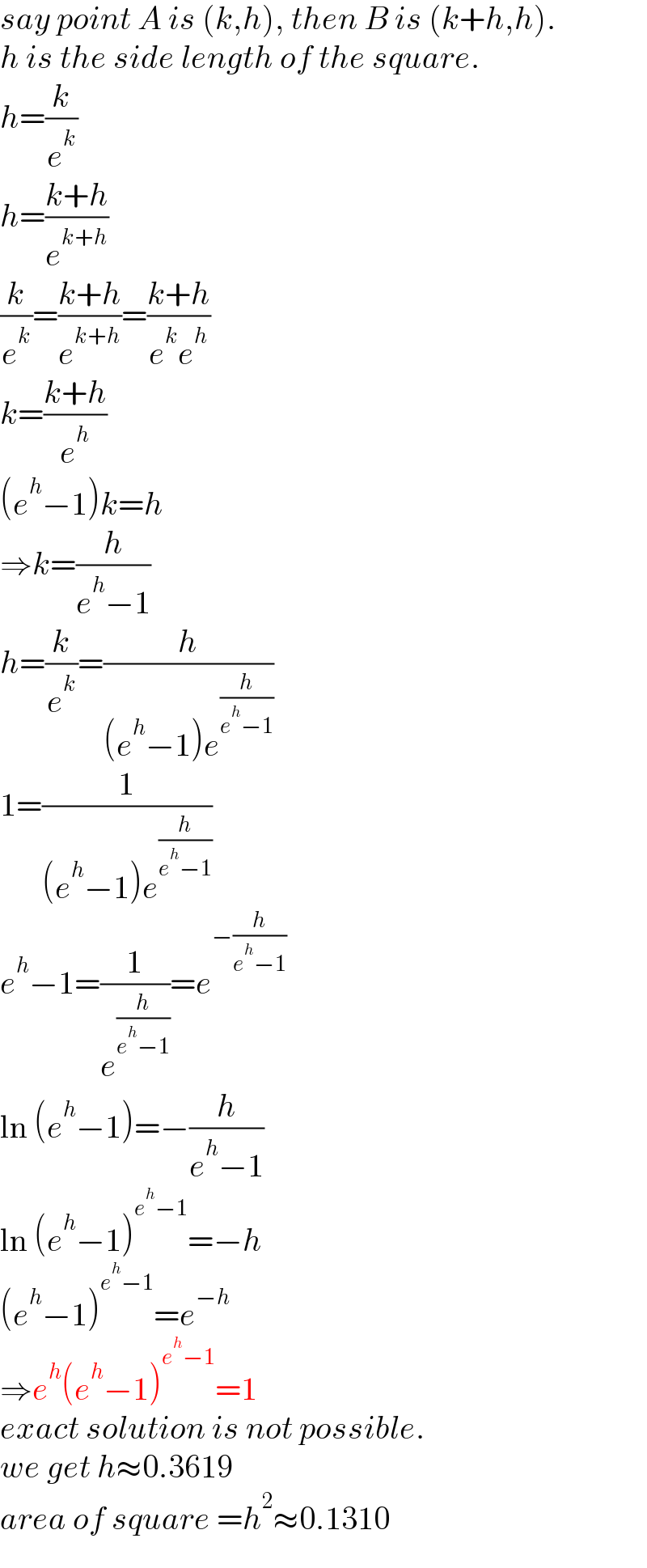
$${say}\:{point}\:{A}\:{is}\:\left({k},{h}\right),\:{then}\:{B}\:{is}\:\left({k}+{h},{h}\right). \\ $$$${h}\:{is}\:{the}\:{side}\:{length}\:{of}\:{the}\:{square}. \\ $$$${h}=\frac{{k}}{{e}^{{k}} } \\ $$$${h}=\frac{{k}+{h}}{{e}^{{k}+{h}} } \\ $$$$\frac{{k}}{{e}^{{k}} }=\frac{{k}+{h}}{{e}^{{k}+{h}} }=\frac{{k}+{h}}{{e}^{{k}} {e}^{{h}} } \\ $$$${k}=\frac{{k}+{h}}{{e}^{{h}} } \\ $$$$\left({e}^{{h}} −\mathrm{1}\right){k}={h} \\ $$$$\Rightarrow{k}=\frac{{h}}{{e}^{{h}} −\mathrm{1}} \\ $$$${h}=\frac{{k}}{{e}^{{k}} }=\frac{{h}}{\left({e}^{{h}} −\mathrm{1}\right){e}^{\frac{{h}}{{e}^{{h}} −\mathrm{1}}} } \\ $$$$\mathrm{1}=\frac{\mathrm{1}}{\left({e}^{{h}} −\mathrm{1}\right){e}^{\frac{{h}}{{e}^{{h}} −\mathrm{1}}} } \\ $$$${e}^{{h}} −\mathrm{1}=\frac{\mathrm{1}}{{e}^{\frac{{h}}{{e}^{{h}} −\mathrm{1}}} }={e}^{−\frac{{h}}{{e}^{{h}} −\mathrm{1}}} \\ $$$$\mathrm{ln}\:\left({e}^{{h}} −\mathrm{1}\right)=−\frac{{h}}{{e}^{{h}} −\mathrm{1}} \\ $$$$\mathrm{ln}\:\left({e}^{{h}} −\mathrm{1}\right)^{{e}^{{h}} −\mathrm{1}} =−{h} \\ $$$$\left({e}^{{h}} −\mathrm{1}\right)^{{e}^{{h}} −\mathrm{1}} ={e}^{−{h}} \\ $$$$\Rightarrow{e}^{{h}} \left({e}^{{h}} −\mathrm{1}\right)^{{e}^{{h}} −\mathrm{1}} =\mathrm{1} \\ $$$${exact}\:{solution}\:{is}\:{not}\:{possible}. \\ $$$${we}\:{get}\:{h}\approx\mathrm{0}.\mathrm{3619} \\ $$$${area}\:{of}\:{square}\:={h}^{\mathrm{2}} \approx\mathrm{0}.\mathrm{1310} \\ $$
Commented by Tawa11 last updated on 27/Dec/21

$$\mathrm{Thanks}\:\mathrm{for}\:\mathrm{your}\:\mathrm{time}\:\mathrm{sir},\:\mathrm{I}\:\mathrm{really}\:\mathrm{appreciate}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by mr W last updated on 27/Dec/21

Commented by mr W last updated on 27/Dec/21
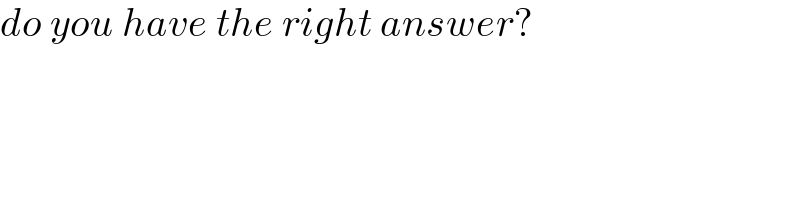
$${do}\:{you}\:{have}\:{the}\:{right}\:{answer}? \\ $$
Commented by Tawa11 last updated on 27/Dec/21

$$\mathrm{No}\:\mathrm{sir},\:\mathrm{I}\:\mathrm{am}\:\mathrm{studying}\:\mathrm{your}\:\mathrm{solution}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
