Question Number 16220 by Mr easymsn last updated on 19/Jun/17
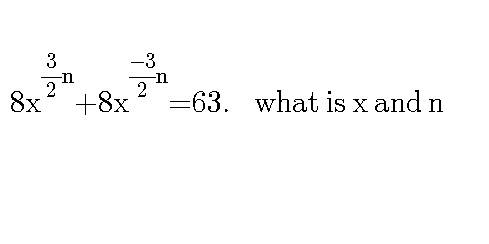
Answered by liday last updated on 19/Jun/17

$$\mathrm{let}\:\mathrm{x}^{\frac{\mathrm{3}}{\mathrm{2}}\mathrm{n}} =\mathrm{a}\:\mathrm{then}\:\mathrm{8a}+\frac{\mathrm{8}}{\mathrm{a}}=\mathrm{63}\:\Rightarrow\mathrm{8a}^{\mathrm{2}} −\mathrm{63a}+\mathrm{8}=\mathrm{0} \\ $$$$\mathrm{a}=\frac{\mathrm{63}\pm\sqrt{\mathrm{63}^{\mathrm{2}} −\mathrm{4}×\mathrm{8}×\mathrm{8}}}{\mathrm{16}}=\frac{\mathrm{63}\pm\sqrt{\mathrm{3713}}}{\mathrm{16}} \\ $$$$\Rightarrow\mathrm{x}^{\frac{\mathrm{3}}{\mathrm{2}}\mathrm{n}} =\frac{\mathrm{63}\pm\sqrt{\mathrm{3713}}}{\mathrm{16}}\Rightarrow\mathrm{x}=\left(\sqrt[{\mathrm{3}}]{\frac{\mathrm{63}\pm\sqrt{\mathrm{3713}}}{\mathrm{16}}}\right)^{\frac{\mathrm{2}}{\mathrm{n}}} \\ $$
