Question Number 162249 by SANOGO last updated on 28/Dec/21
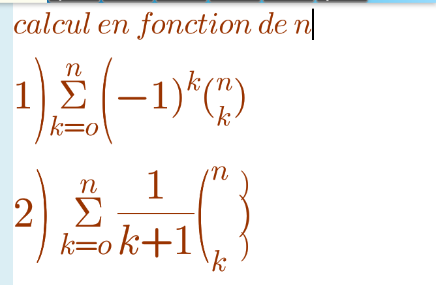
Answered by mr W last updated on 28/Dec/21
![(1) Σ_(k=0) ^n ((n),(k) ) x^k =(1+x)^n set x=−1 ⇒Σ_(k=0) ^n (−1)^k ((n),(k) ) =0 lim_(n→∞) Σ_(k=0) ^n (−1)^k ((n),(k) ) =lim_(n→∞) 0=0 (2) Σ_(k=0) ^n ((n),(k) ) x^k =(1+x)^n Σ_(k=0) ^n ((n),(k) ) ∫_0 ^x x^k dx=∫_0 ^x (1+x)^n dx Σ_(k=0) ^n ((n),(k) ) (x^(k+1) /(k+1))=[(((1+x)^(n+1) )/(n+1))]_0 ^x Σ_(k=0) ^n ((n),(k) ) (x^(k+1) /(k+1))=(((1+x)^(n+1) −1)/(n+1)) set x=1 ⇒Σ_(k=0) ^n (1/(k+1)) ((n),(k) ) =((2^(n+1) −1)/(n+1))](https://www.tinkutara.com/question/Q162252.png)
$$\left(\mathrm{1}\right) \\ $$$$\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}\:{x}^{{k}} =\left(\mathrm{1}+{x}\right)^{{n}} \\ $$$${set}\:{x}=−\mathrm{1} \\ $$$$\Rightarrow\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\left(−\mathrm{1}\right)^{{k}} \begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}\:=\mathrm{0} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\left(−\mathrm{1}\right)^{{k}} \begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}\:=\underset{{n}\rightarrow\infty} {\mathrm{lim}0}=\mathrm{0} \\ $$$$ \\ $$$$\left(\mathrm{2}\right) \\ $$$$\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}\:{x}^{{k}} =\left(\mathrm{1}+{x}\right)^{{n}} \\ $$$$\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}\:\int_{\mathrm{0}} ^{{x}} {x}^{{k}} {dx}=\int_{\mathrm{0}} ^{{x}} \left(\mathrm{1}+{x}\right)^{{n}} {dx} \\ $$$$\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}\:\frac{{x}^{{k}+\mathrm{1}} }{{k}+\mathrm{1}}=\left[\frac{\left(\mathrm{1}+{x}\right)^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}\right]_{\mathrm{0}} ^{{x}} \\ $$$$\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}\:\frac{{x}^{{k}+\mathrm{1}} }{{k}+\mathrm{1}}=\frac{\left(\mathrm{1}+{x}\right)^{{n}+\mathrm{1}} −\mathrm{1}}{{n}+\mathrm{1}} \\ $$$${set}\:{x}=\mathrm{1} \\ $$$$\Rightarrow\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\:\frac{\mathrm{1}}{{k}+\mathrm{1}}\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}\:=\frac{\mathrm{2}^{{n}+\mathrm{1}} −\mathrm{1}}{{n}+\mathrm{1}} \\ $$
Commented by SANOGO last updated on 28/Dec/21
$${merci}\:{bien} \\ $$
