Question Number 162344 by stelor last updated on 28/Dec/21

Commented by mr W last updated on 29/Dec/21
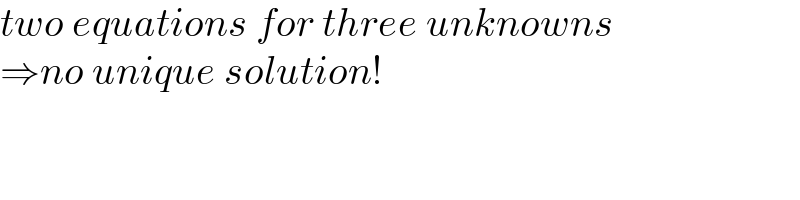
$${two}\:{equations}\:{for}\:{three}\:{unknowns} \\ $$$$\Rightarrow{no}\:{unique}\:{solution}! \\ $$
Answered by aleks041103 last updated on 29/Dec/21
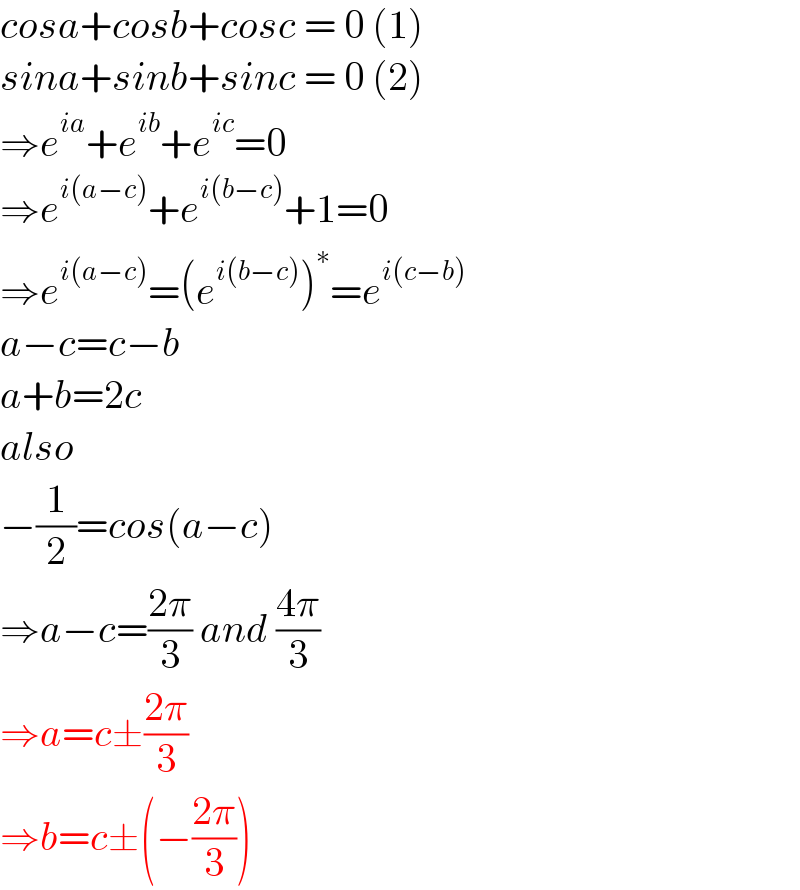
$${cosa}+{cosb}+{cosc}\:=\:\mathrm{0}\:\left(\mathrm{1}\right) \\ $$$${sina}+{sinb}+{sinc}\:=\:\mathrm{0}\:\left(\mathrm{2}\right) \\ $$$$\Rightarrow{e}^{{ia}} +{e}^{{ib}} +{e}^{{ic}} =\mathrm{0} \\ $$$$\Rightarrow{e}^{{i}\left({a}−{c}\right)} +{e}^{{i}\left({b}−{c}\right)} +\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow{e}^{{i}\left({a}−{c}\right)} =\left({e}^{{i}\left({b}−{c}\right)} \right)^{\ast} ={e}^{{i}\left({c}−{b}\right)} \\ $$$${a}−{c}={c}−{b} \\ $$$${a}+{b}=\mathrm{2}{c} \\ $$$${also} \\ $$$$−\frac{\mathrm{1}}{\mathrm{2}}={cos}\left({a}−{c}\right) \\ $$$$\Rightarrow{a}−{c}=\frac{\mathrm{2}\pi}{\mathrm{3}}\:{and}\:\frac{\mathrm{4}\pi}{\mathrm{3}} \\ $$$$\Rightarrow{a}={c}\pm\frac{\mathrm{2}\pi}{\mathrm{3}} \\ $$$$\Rightarrow{b}={c}\pm\left(−\frac{\mathrm{2}\pi}{\mathrm{3}}\right) \\ $$
Commented by aleks041103 last updated on 29/Dec/21

$${this}\:{has}\:{a}\:{cute}\:{geometric}\:{proof}\:{too}. \\ $$$${the}\:{complex}\:{vectors}\:{e}^{{ia}} ,\:{e}^{{ib}} ,\:{e}^{{ic}} \:{must} \\ $$$${sum}\:{up}\:{to}\:\mathrm{0}\:{and}\:{have}\:{the}\:{same}\:{length}. \\ $$$${Therefore}\:{the}\:{tree}\:{vectors}\:{must}\:{be}\:{symmetric} \\ $$$$\Rightarrow\:{the}\:{angle}\:{between}\:{any}\:{two}\:{of}\:{them} \\ $$$${must}\:{be}\:\frac{\mathrm{360}°}{\mathrm{3}}=\mathrm{120}°. \\ $$
