Question Number 162348 by smallEinstein last updated on 29/Dec/21

Commented by mr W last updated on 29/Dec/21

$${Einstein}\:{sir}:\:{can}\:{you}\:{please}\:{crop}\:{the} \\ $$$${image}\:{properly}\:{when}\:{uploading}\:{it}? \\ $$
Commented by Rasheed.Sindhi last updated on 29/Dec/21

$$\mathrm{Too}\:\mathrm{much}\:\mathrm{waste}\:\mathrm{of}\:\mathrm{black}\:\mathrm{colour}!!! \\ $$$$\mathrm{Too}\:\mathrm{much}\:\mathrm{waste}\:\mathrm{of}\:\mathrm{space}!!! \\ $$⬛⬛⬛⬛⬛⬛⬛⬛⬛⬛⬛⬛⬛⬛⬛
⬛😭😭😭⬛⬛⬛⬛⬛⬛⬛⬛⬛⬛⬛
⬛😭😭😭⬛⬛⬛⬛⬛⬛⬛⬛⬛⬛⬛
Commented by mr W last updated on 29/Dec/21

$${the}\:{main}\:{problem}\:{is}\:{that}\:{you}\:{can}'{t} \\ $$$${see}\:{the}\:{actual}\:{question}\:{when}\:{you}\:{are} \\ $$$${answering}\:{such}\:{a}\:{badly}\:{posted}\: \\ $$$${question}.\: \\ $$$${this}\:{is}\:{what}\:{i}\:{mean}: \\ $$
Commented by mr W last updated on 29/Dec/21

Answered by Ar Brandon last updated on 24/Mar/22
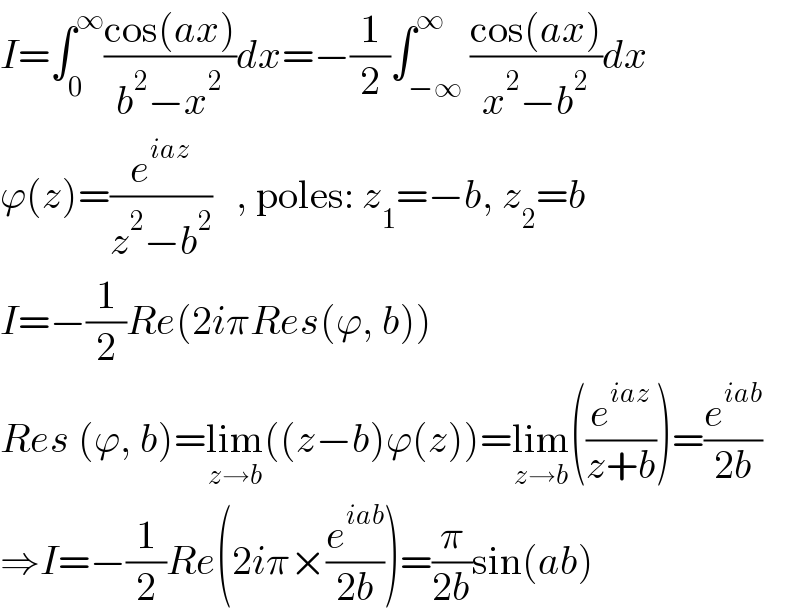
$${I}=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{cos}\left({ax}\right)}{{b}^{\mathrm{2}} −{x}^{\mathrm{2}} }{dx}=−\frac{\mathrm{1}}{\mathrm{2}}\int_{−\infty} ^{\infty} \frac{\mathrm{cos}\left({ax}\right)}{{x}^{\mathrm{2}} −{b}^{\mathrm{2}} }{dx} \\ $$$$\varphi\left({z}\right)=\frac{{e}^{{iaz}} }{{z}^{\mathrm{2}} −{b}^{\mathrm{2}} }\:\:\:,\:\mathrm{poles}:\:{z}_{\mathrm{1}} =−{b},\:{z}_{\mathrm{2}} ={b} \\ $$$${I}=−\frac{\mathrm{1}}{\mathrm{2}}{Re}\left(\mathrm{2}{i}\pi{Res}\left(\varphi,\:{b}\right)\right) \\ $$$${Res}\:\left(\varphi,\:{b}\right)=\underset{{z}\rightarrow{b}} {\mathrm{lim}}\left(\left({z}−{b}\right)\varphi\left({z}\right)\right)=\underset{{z}\rightarrow{b}} {\mathrm{lim}}\left(\frac{{e}^{{iaz}} }{{z}+{b}}\right)=\frac{{e}^{{iab}} }{\mathrm{2}{b}} \\ $$$$\Rightarrow{I}=−\frac{\mathrm{1}}{\mathrm{2}}{Re}\left(\mathrm{2}{i}\pi×\frac{{e}^{{iab}} }{\mathrm{2}{b}}\right)=\frac{\pi}{\mathrm{2}{b}}\mathrm{sin}\left({ab}\right) \\ $$
