Menu Close

Question-162368

Tinku Tara 0 Comments
Pin




Question Number 162368 by mr W last updated on 29/Dec/21
Commented by mr W last updated on 29/Dec/21
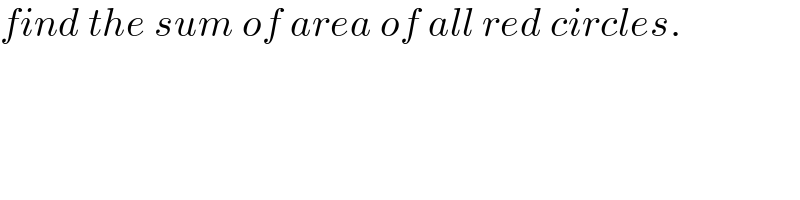
find the sum of area of all red circles.
$${find}\:{the}\:{sum}\:{of}\:{area}\:{of}\:{all}\:{red}\:{circles}. \\ $$
Commented by mr W last updated on 29/Dec/21
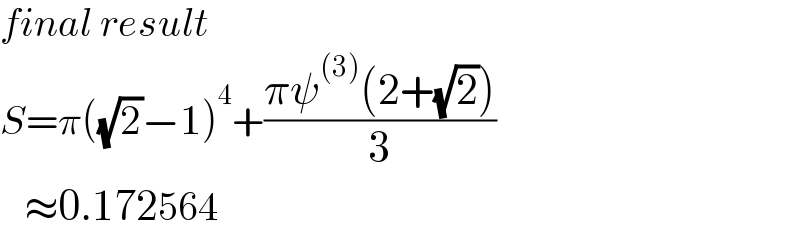
final result S=π((√2)−1)^4 +((πψ^((3)) (2+(√2)))/3) ≈0.172564
$${final}\:{result} \\ $$$${S}=\pi\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)^{\mathrm{4}} +\frac{\pi\psi^{\left(\mathrm{3}\right)} \left(\mathrm{2}+\sqrt{\mathrm{2}}\right)}{\mathrm{3}} \\ $$$$\:\:\:\approx\mathrm{0}.\mathrm{172564} \\ $$
Answered by aleks041103 last updated on 29/Dec/21
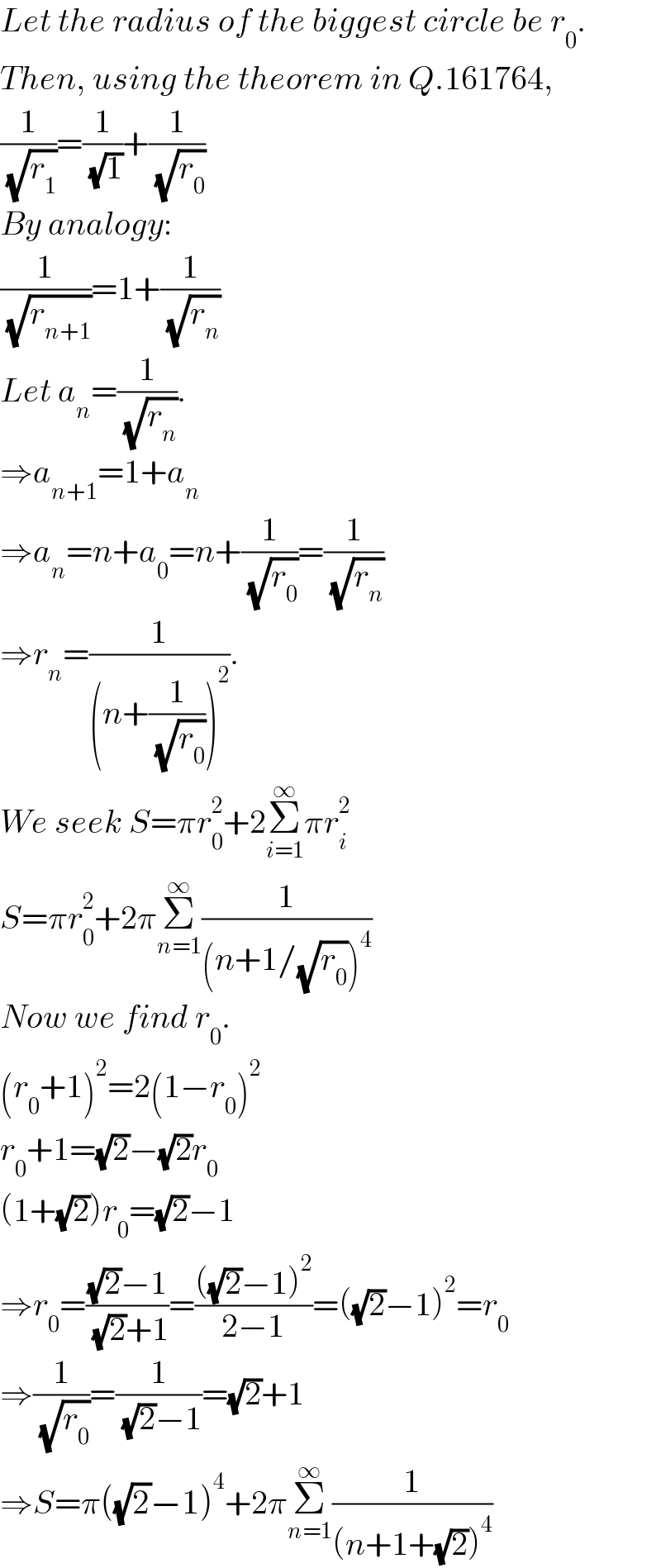
Let the radius of the biggest circle be r_0 . Then, using the theorem in Q.161764, (1/( (√r_1 )))=(1/( (√1)))+(1/( (√r_0 ))) By analogy: (1/( (√r_(n+1) )))=1+(1/( (√r_n ))) Let a_n =(1/( (√r_n ))). ⇒a_(n+1) =1+a_n ⇒a_n =n+a_0 =n+(1/( (√r_0 )))=(1/( (√r_n ))) ⇒r_n =(1/((n+(1/( (√r_0 ))))^2 )). We seek S=πr_0 ^2 +2Σ_(i=1) ^∞ πr_i ^2 S=πr_0 ^2 +2πΣ_(n=1) ^∞ (1/((n+1/(√r_0 ))^4 )) Now we find r_0 . (r_0 +1)^2 =2(1−r_0 )^2 r_0 +1=(√2)−(√2)r_0 (1+(√2))r_0 =(√2)−1 ⇒r_0 =(((√2)−1)/( (√2)+1))=((((√2)−1)^2 )/(2−1))=((√2)−1)^2 =r_0 ⇒(1/( (√r_0 )))=(1/( (√2)−1))=(√2)+1 ⇒S=π((√2)−1)^4 +2πΣ_(n=1) ^∞ (1/((n+1+(√2))^4 ))
$${Let}\:{the}\:{radius}\:{of}\:{the}\:{biggest}\:{circle}\:{be}\:{r}_{\mathrm{0}} . \\ $$$${Then},\:{using}\:{the}\:{theorem}\:{in}\:{Q}.\mathrm{161764}, \\ $$$$\frac{\mathrm{1}}{\:\sqrt{{r}_{\mathrm{1}} }}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}}}+\frac{\mathrm{1}}{\:\sqrt{{r}_{\mathrm{0}} }} \\ $$$${By}\:{analogy}: \\ $$$$\frac{\mathrm{1}}{\:\sqrt{{r}_{{n}+\mathrm{1}} }}=\mathrm{1}+\frac{\mathrm{1}}{\:\sqrt{{r}_{{n}} }} \\ $$$${Let}\:{a}_{{n}} =\frac{\mathrm{1}}{\:\sqrt{{r}_{{n}} }}. \\ $$$$\Rightarrow{a}_{{n}+\mathrm{1}} =\mathrm{1}+{a}_{{n}} \\ $$$$\Rightarrow{a}_{{n}} ={n}+{a}_{\mathrm{0}} ={n}+\frac{\mathrm{1}}{\:\sqrt{{r}_{\mathrm{0}} }}=\frac{\mathrm{1}}{\:\sqrt{{r}_{{n}} }} \\ $$$$\Rightarrow{r}_{{n}} =\frac{\mathrm{1}}{\left({n}+\frac{\mathrm{1}}{\:\sqrt{{r}_{\mathrm{0}} }}\right)^{\mathrm{2}} }. \\ $$$${We}\:{seek}\:{S}=\pi{r}_{\mathrm{0}} ^{\mathrm{2}} +\mathrm{2}\underset{{i}=\mathrm{1}} {\overset{\infty} {\sum}}\pi{r}_{{i}} ^{\mathrm{2}} \\ $$$${S}=\pi{r}_{\mathrm{0}} ^{\mathrm{2}} +\mathrm{2}\pi\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({n}+\mathrm{1}/\sqrt{{r}_{\mathrm{0}} }\right)^{\mathrm{4}} } \\ $$$${Now}\:{we}\:{find}\:{r}_{\mathrm{0}} . \\ $$$$\left({r}_{\mathrm{0}} +\mathrm{1}\right)^{\mathrm{2}} =\mathrm{2}\left(\mathrm{1}−{r}_{\mathrm{0}} \right)^{\mathrm{2}} \\ $$$${r}_{\mathrm{0}} +\mathrm{1}=\sqrt{\mathrm{2}}−\sqrt{\mathrm{2}}{r}_{\mathrm{0}} \\ $$$$\left(\mathrm{1}+\sqrt{\mathrm{2}}\right){r}_{\mathrm{0}} =\sqrt{\mathrm{2}}−\mathrm{1} \\ $$$$\Rightarrow{r}_{\mathrm{0}} =\frac{\sqrt{\mathrm{2}}−\mathrm{1}}{\:\sqrt{\mathrm{2}}+\mathrm{1}}=\frac{\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{2}−\mathrm{1}}=\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)^{\mathrm{2}} ={r}_{\mathrm{0}} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\:\sqrt{{r}_{\mathrm{0}} }}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}−\mathrm{1}}=\sqrt{\mathrm{2}}+\mathrm{1} \\ $$$$\Rightarrow{S}=\pi\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)^{\mathrm{4}} +\mathrm{2}\pi\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({n}+\mathrm{1}+\sqrt{\mathrm{2}}\right)^{\mathrm{4}} } \\ $$
Commented by mr W last updated on 29/Dec/21
also this is perfect! congratulations for the perfect solution sir!
$${also}\:{this}\:{is}\:{perfect}!\:{congratulations} \\ $$$${for}\:{the}\:{perfect}\:{solution}\:{sir}! \\ $$
Commented by mr W last updated on 29/Dec/21
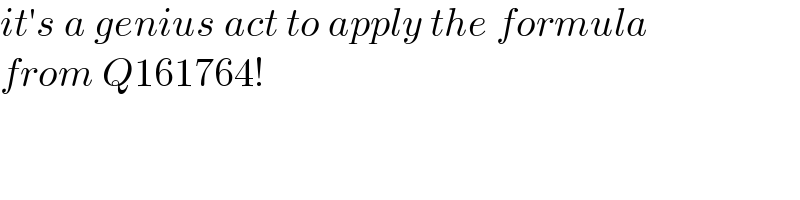
it′s a genius act to apply the formula from Q161764!
$${it}'{s}\:{a}\:{genius}\:{act}\:{to}\:{apply}\:{the}\:{formula} \\ $$$${from}\:{Q}\mathrm{161764}! \\ $$
Commented by aleks041103 last updated on 29/Dec/21
Lets find the sum Σ_(n=1) ^∞ (1/((n+k)^4 ))=s ψ_0 (z)=(1/(Γ(z))) ((dΓ(z))/dz) − digamma function define ψ_n (z)=((d^n ψ_0 (z))/dz^n ) It is kown that ψ_n (z)=(−1)^(n+1) n!Σ_(k=0) ^∞ (1/((z+k)^(n+1) )) ⇒ψ_3 (a)=6Σ_(n=0) ^∞ (1/((n+a)^4 )) ⇒Σ_(n=1) ^∞ (1/((n+a)^4 ))=((ψ_3 (a))/6)−(1/a^4 )
$${Lets}\:{find}\:{the}\:{sum} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({n}+{k}\right)^{\mathrm{4}} }={s} \\ $$$$\psi_{\mathrm{0}} \left({z}\right)=\frac{\mathrm{1}}{\Gamma\left({z}\right)}\:\frac{{d}\Gamma\left({z}\right)}{{dz}}\:−\:{digamma}\:{function} \\ $$$${define} \\ $$$$\psi_{{n}} \left({z}\right)=\frac{{d}^{{n}} \psi_{\mathrm{0}} \left({z}\right)}{{dz}^{{n}} } \\ $$$${It}\:{is}\:{kown}\:{that}\: \\ $$$$\psi_{{n}} \left({z}\right)=\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} {n}!\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({z}+{k}\right)^{{n}+\mathrm{1}} } \\ $$$$\Rightarrow\psi_{\mathrm{3}} \left({a}\right)=\mathrm{6}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({n}+{a}\right)^{\mathrm{4}} } \\ $$$$\Rightarrow\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({n}+{a}\right)^{\mathrm{4}} }=\frac{\psi_{\mathrm{3}} \left({a}\right)}{\mathrm{6}}−\frac{\mathrm{1}}{{a}^{\mathrm{4}} } \\ $$
Commented by aleks041103 last updated on 29/Dec/21
to be continued
$${to}\:{be}\:{continued} \\ $$
Commented by mr W last updated on 29/Dec/21
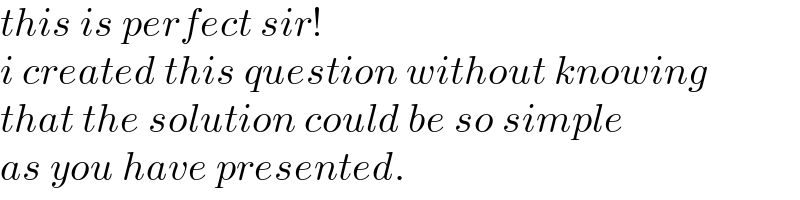
this is perfect sir! i created this question without knowing that the solution could be so simple as you have presented.
$${this}\:{is}\:{perfect}\:{sir}! \\ $$$${i}\:{created}\:{this}\:{question}\:{without}\:{knowing} \\ $$$${that}\:{the}\:{solution}\:{could}\:{be}\:{so}\:{simple} \\ $$$${as}\:{you}\:{have}\:{presented}. \\ $$
Commented by aleks041103 last updated on 29/Dec/21
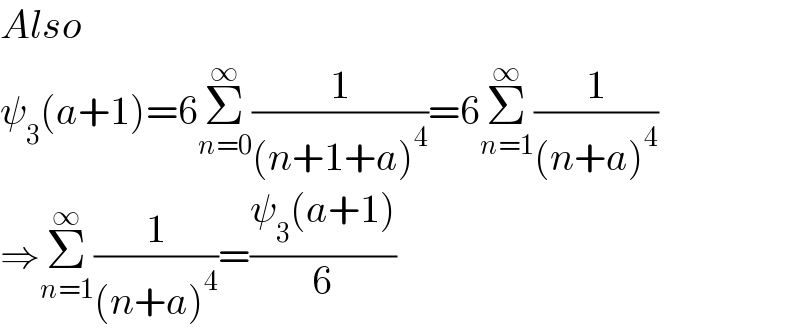
Also ψ_3 (a+1)=6Σ_(n=0) ^∞ (1/((n+1+a)^4 ))=6Σ_(n=1) ^∞ (1/((n+a)^4 )) ⇒Σ_(n=1) ^∞ (1/((n+a)^4 ))=((ψ_3 (a+1))/6)
$${Also} \\ $$$$\psi_{\mathrm{3}} \left({a}+\mathrm{1}\right)=\mathrm{6}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({n}+\mathrm{1}+{a}\right)^{\mathrm{4}} }=\mathrm{6}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({n}+{a}\right)^{\mathrm{4}} } \\ $$$$\Rightarrow\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({n}+{a}\right)^{\mathrm{4}} }=\frac{\psi_{\mathrm{3}} \left({a}+\mathrm{1}\right)}{\mathrm{6}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *