Question Number 162481 by mnjuly1970 last updated on 29/Dec/21
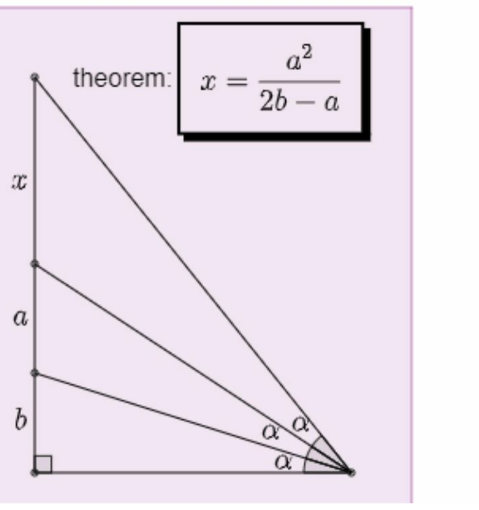
Answered by mr W last updated on 29/Dec/21

$${length}\:{of}\:{base}\:={h} \\ $$$$\mathrm{tan}\:\alpha=\frac{{b}}{{h}} \\ $$$$\mathrm{tan}\:\mathrm{2}\alpha=\frac{{b}+{a}}{{h}} \\ $$$$\mathrm{tan}\:\mathrm{3}\alpha=\frac{{b}+{a}+{x}}{{h}} \\ $$$$\mathrm{tan}\:\mathrm{2}\alpha=\frac{\mathrm{2}\:\mathrm{tan}\:\alpha}{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \:\alpha} \\ $$$$\frac{{b}+{a}}{{h}}=\frac{\mathrm{2}×\frac{{b}}{{h}}}{\mathrm{1}−\frac{{b}^{\mathrm{2}} }{{h}^{\mathrm{2}} }} \\ $$$${b}+{a}=\frac{\mathrm{2}{bh}^{\mathrm{2}} }{{h}^{\mathrm{2}} −{b}^{\mathrm{2}} } \\ $$$$\Rightarrow{h}^{\mathrm{2}} =\frac{\left({a}+{b}\right){b}^{\mathrm{2}} }{{a}−{b}} \\ $$$$\mathrm{tan}\:\mathrm{3}\alpha=\frac{\mathrm{tan}\:\mathrm{2}\alpha+\mathrm{tan}\:\alpha}{\mathrm{1}−\mathrm{tan}\:\mathrm{2}\alpha\:\mathrm{tan}\:\alpha} \\ $$$${x}=\frac{\left({a}+\mathrm{2}{b}\right){h}^{\mathrm{2}} }{{h}^{\mathrm{2}} −\left({a}+{b}\right){b}}−\left({a}+{b}\right) \\ $$$${x}=\frac{\left({a}+\mathrm{2}{b}\right)}{\mathrm{1}−\left({a}+{b}\right){b}×\frac{\left({a}−{b}\right)}{\left({a}+{b}\right){b}^{\mathrm{2}} }}−\left({a}+{b}\right) \\ $$$${x}=\frac{\left({a}+\mathrm{2}{b}\right){b}}{\mathrm{2}{b}−{a}}−\left({a}+{b}\right) \\ $$$${x}=\frac{{a}^{\mathrm{2}} }{\mathrm{2}{b}−{a}}\:\checkmark \\ $$
Commented by mnjuly1970 last updated on 29/Dec/21

$$\:\:{grateful} \\ $$
Commented by Tawa11 last updated on 30/Dec/21

$$\mathrm{Great}\:\mathrm{sir} \\ $$
