Question-162490

Question Number 162490 by amin96 last updated on 29/Dec/21

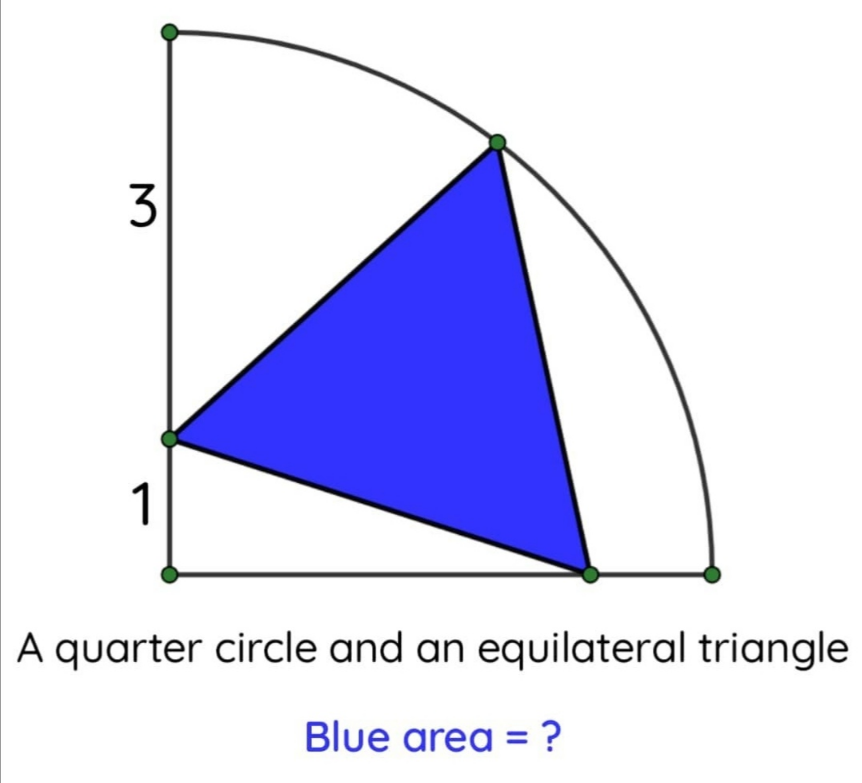
Answered by mr W last updated on 30/Dec/21

Commented by mr W last updated on 30/Dec/21

R=4=radius OA=a=1 s=side length of equilateral OC=(√(s^2 −a^2 )) DC=s cos ((π/3)+α)=(1/2)(s cos α−(√3) s sin α) =(1/2)((√(s^2 −a^2 ))−(√3) a) DB=s sin ((π/3)+α)=(1/2)((√3) s cos α+s sin α) =(1/2)((√(3(s^2 −a^2 )))+a) OD=(√(s^2 −a^2 ))− (1/2)((√(s^2 −a^2 ))−(√3) a) = (1/2)((√(s^2 −a^2 ))+(√3) a) OD^2 +DB^2 =OB^2 (1/4)((√(s^2 −a^2 ))+(√3) a)^2 +(1/4)((√(3(s^2 −a^2 )))+a)^2 =R^2 s^2 −a^2 +3a^2 +2a(√(3(s^2 −a^2 )))+3(s^2 −a^2 )+a^2 +2a(√(3(s^2 −a^2 )))=4R^2 a(√(3(s^2 −a^2 )))=R^2 −s^2 3a^2 (s^2 −a^2 )=s^4 +R^4 −2R^2 s^2 s^4 −(2R^2 +3a^2 )s^2 +R^4 +3a^4 =0 s^2 =((2R^2 +3a^2 −(√((2R^2 +3a^2 )^2 −4(R^4 +3a^4 ))))/2) =((2R^2 +3a^2 −a(√(3(4R^2 −a^2 ))))/2) with R=4, a=1: s^2 =((2×4^2 +3×1^2 −1(√(3(4×4^2 −1^2 ))))/2)=((35−3(√(21)))/2) area of blue equilateral A_(blue) =(((√3)s^2 )/4)=(((√3)(35−3(√(21))))/8)=((35(√3)−9(√7))/8)≈4.601 =================== let ξ=(a/R) ((s/R))^2 =((2+3ξ^2 −ξ(√(3(4−ξ^2 ))))/2) ((s/R))_(max) =1 at ξ=0 ((s/R))_(min) =(√3)−1 at ξ=(((√3)−1)/( (√2)))

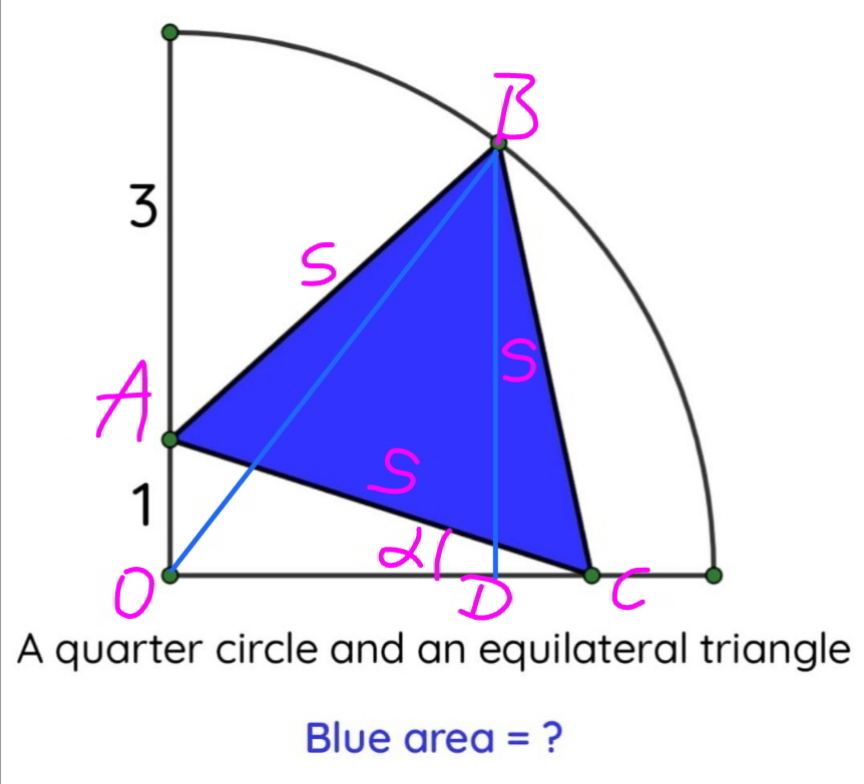
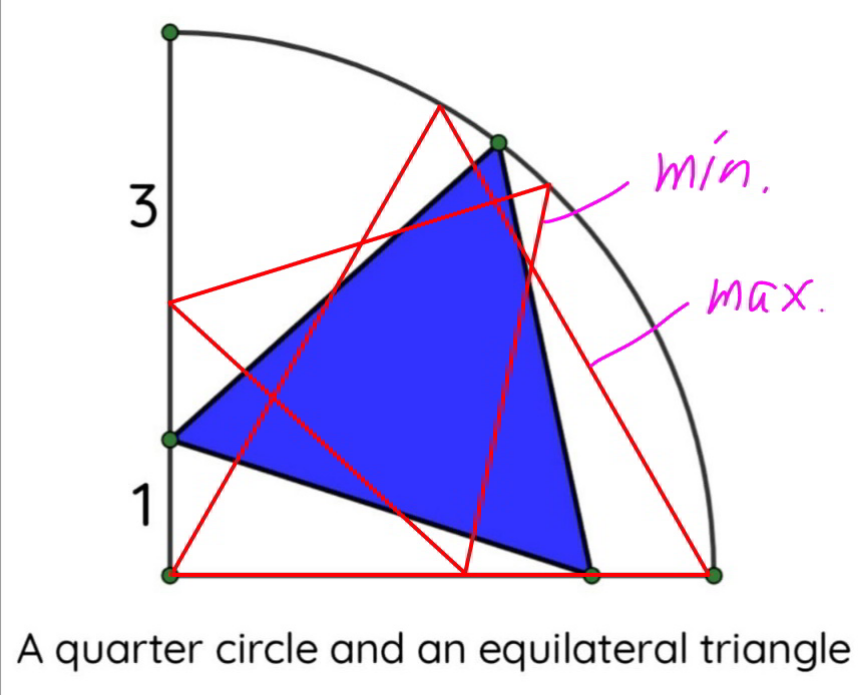
$${R}=\mathrm{4}={radius} \\ $$$${OA}={a}=\mathrm{1} \\ $$$${s}={side}\:{length}\:{of}\:{equilateral} \\ $$$${OC}=\sqrt{{s}^{\mathrm{2}} −{a}^{\mathrm{2}} } \\ $$$${DC}={s}\:\mathrm{cos}\:\left(\frac{\pi}{\mathrm{3}}+\alpha\right)=\frac{\mathrm{1}}{\mathrm{2}}\left({s}\:\mathrm{cos}\:\alpha−\sqrt{\mathrm{3}}\:{s}\:\mathrm{sin}\:\alpha\right) \\ $$$$\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\left(\sqrt{{s}^{\mathrm{2}} −{a}^{\mathrm{2}} }−\sqrt{\mathrm{3}}\:{a}\right) \\ $$$${DB}={s}\:\mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}+\alpha\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\sqrt{\mathrm{3}}\:{s}\:\mathrm{cos}\:\alpha+{s}\:\mathrm{sin}\:\alpha\right) \\ $$$$\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\left(\sqrt{\mathrm{3}\left({s}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)}+{a}\right) \\ $$$${OD}=\sqrt{{s}^{\mathrm{2}} −{a}^{\mathrm{2}} }−\:\frac{\mathrm{1}}{\mathrm{2}}\left(\sqrt{{s}^{\mathrm{2}} −{a}^{\mathrm{2}} }−\sqrt{\mathrm{3}}\:{a}\right) \\ $$$$\:\:\:\:\:\:\:=\:\frac{\mathrm{1}}{\mathrm{2}}\left(\sqrt{{s}^{\mathrm{2}} −{a}^{\mathrm{2}} }+\sqrt{\mathrm{3}}\:{a}\right) \\ $$$${OD}^{\mathrm{2}} +{DB}^{\mathrm{2}} ={OB}^{\mathrm{2}} \\ $$$$\:\frac{\mathrm{1}}{\mathrm{4}}\left(\sqrt{{s}^{\mathrm{2}} −{a}^{\mathrm{2}} }+\sqrt{\mathrm{3}}\:{a}\right)^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{4}}\left(\sqrt{\mathrm{3}\left({s}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)}+{a}\right)^{\mathrm{2}} ={R}^{\mathrm{2}} \\ $$$$\:{s}^{\mathrm{2}} −{a}^{\mathrm{2}} +\mathrm{3}{a}^{\mathrm{2}} +\mathrm{2}{a}\sqrt{\mathrm{3}\left({s}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)}+\mathrm{3}\left({s}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)+{a}^{\mathrm{2}} +\mathrm{2}{a}\sqrt{\mathrm{3}\left({s}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)}=\mathrm{4}{R}^{\mathrm{2}} \\ $$$$\:{a}\sqrt{\mathrm{3}\left({s}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)}={R}^{\mathrm{2}} −{s}^{\mathrm{2}} \\ $$$$\:\mathrm{3}{a}^{\mathrm{2}} \left({s}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)={s}^{\mathrm{4}} +{R}^{\mathrm{4}} −\mathrm{2}{R}^{\mathrm{2}} {s}^{\mathrm{2}} \\ $$$$\:{s}^{\mathrm{4}} −\left(\mathrm{2}{R}^{\mathrm{2}} +\mathrm{3}{a}^{\mathrm{2}} \right){s}^{\mathrm{2}} +{R}^{\mathrm{4}} +\mathrm{3}{a}^{\mathrm{4}} =\mathrm{0} \\ $$$${s}^{\mathrm{2}} =\frac{\mathrm{2}{R}^{\mathrm{2}} +\mathrm{3}{a}^{\mathrm{2}} −\sqrt{\left(\mathrm{2}{R}^{\mathrm{2}} +\mathrm{3}{a}^{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{4}\left({R}^{\mathrm{4}} +\mathrm{3}{a}^{\mathrm{4}} \right)}}{\mathrm{2}} \\ $$$$\:\:\:\:=\frac{\mathrm{2}{R}^{\mathrm{2}} +\mathrm{3}{a}^{\mathrm{2}} −{a}\sqrt{\mathrm{3}\left(\mathrm{4}{R}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)}}{\mathrm{2}} \\ $$$${with}\:{R}=\mathrm{4},\:{a}=\mathrm{1}: \\ $$$${s}^{\mathrm{2}} =\frac{\mathrm{2}×\mathrm{4}^{\mathrm{2}} +\mathrm{3}×\mathrm{1}^{\mathrm{2}} −\mathrm{1}\sqrt{\mathrm{3}\left(\mathrm{4}×\mathrm{4}^{\mathrm{2}} −\mathrm{1}^{\mathrm{2}} \right)}}{\mathrm{2}}=\frac{\mathrm{35}−\mathrm{3}\sqrt{\mathrm{21}}}{\mathrm{2}} \\ $$$${area}\:{of}\:{blue}\:{equilateral} \\ $$$${A}_{{blue}} =\frac{\sqrt{\mathrm{3}}{s}^{\mathrm{2}} }{\mathrm{4}}=\frac{\sqrt{\mathrm{3}}\left(\mathrm{35}−\mathrm{3}\sqrt{\mathrm{21}}\right)}{\mathrm{8}}=\frac{\mathrm{35}\sqrt{\mathrm{3}}−\mathrm{9}\sqrt{\mathrm{7}}}{\mathrm{8}}\approx\mathrm{4}.\mathrm{601} \\ $$$$ \\ $$$$=================== \\ $$$${let}\:\xi=\frac{{a}}{{R}} \\ $$$$\left(\frac{{s}}{{R}}\right)^{\mathrm{2}} =\frac{\mathrm{2}+\mathrm{3}\xi^{\mathrm{2}} −\xi\sqrt{\mathrm{3}\left(\mathrm{4}−\xi^{\mathrm{2}} \right)}}{\mathrm{2}} \\ $$$$\left(\frac{{s}}{{R}}\right)_{{max}} =\mathrm{1}\:{at}\:\xi=\mathrm{0} \\ $$$$\left(\frac{{s}}{{R}}\right)_{{min}} =\sqrt{\mathrm{3}}−\mathrm{1}\:{at}\:\xi=\frac{\sqrt{\mathrm{3}}−\mathrm{1}}{\:\sqrt{\mathrm{2}}} \\ $$

Commented by mr W last updated on 30/Dec/21