Question-162530

Question Number 162530 by mr W last updated on 30/Dec/21

Commented by mr W last updated on 30/Dec/21

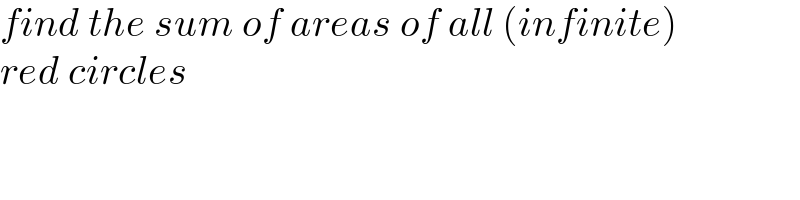
$${find}\:{the}\:{sum}\:{of}\:{areas}\:{of}\:{all}\:\left({infinite}\right) \\ $$$${red}\:{circles} \\ $$

Commented by aleks041103 last updated on 30/Dec/21

$${This}\:{is}\:{a}\:{very}\:{difficult}\:{question}. \\ $$$${Up}\:{untill}\:{now}\:{I}\:{could}\:{only}\:{prove}\:{that}\: \\ $$$${the}\:{centers}\:{lie}\:{on}\:{a}\:{parabola}. \\ $$

Commented by mr W last updated on 30/Dec/21

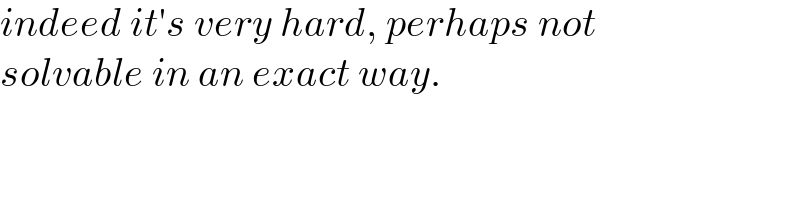
$${indeed}\:{it}'{s}\:{very}\:{hard},\:{perhaps}\:{not} \\ $$$${solvable}\:{in}\:{an}\:{exact}\:{way}. \\ $$

Commented by aleks041103 last updated on 30/Dec/21

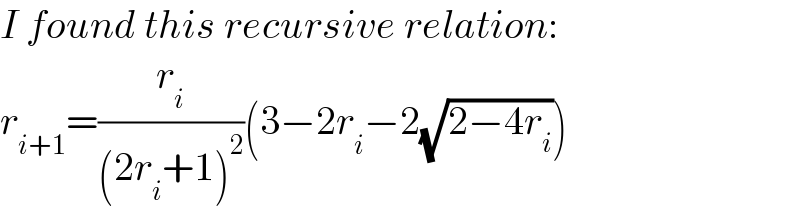
$${I}\:{found}\:{this}\:{recursive}\:{relation}: \\ $$$${r}_{{i}+\mathrm{1}} =\frac{{r}_{{i}} }{\left(\mathrm{2}{r}_{{i}} +\mathrm{1}\right)^{\mathrm{2}} }\left(\mathrm{3}−\mathrm{2}{r}_{{i}} −\mathrm{2}\sqrt{\mathrm{2}−\mathrm{4}{r}_{{i}} }\right) \\ $$

Commented by mr W last updated on 30/Dec/21

$${i}\:{got}\:{this}\:{too}. \\ $$$$\frac{\lambda_{{n}+\mathrm{1}} }{\lambda_{{n}} }=\frac{\mathrm{3}−\mathrm{2}\lambda_{{n}} −\mathrm{2}\sqrt{\mathrm{2}\left(\mathrm{1}−\mathrm{2}\lambda_{{n}} \right)}}{\left(\mathrm{2}\lambda_{{n}} +\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${with}\:\lambda_{{n}} =\frac{{r}_{{n}} }{{R}},\:{R}={radius}\:{of}\:{semicircle}=\mathrm{1} \\ $$$${r}_{\mathrm{0}} =\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${r}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{4}} \\ $$$${r}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{18}} \\ $$$${r}_{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{100}} \\ $$$${r}_{\mathrm{4}} =\frac{\mathrm{1}}{\mathrm{578}} \\ $$$${r}_{\mathrm{5}} =\frac{\mathrm{1}}{\mathrm{3}\:\mathrm{364}} \\ $$$${r}_{\mathrm{6}} =\frac{\mathrm{1}}{\mathrm{19}\:\mathrm{602}} \\ $$$${r}_{\mathrm{7}} =\frac{\mathrm{1}}{\mathrm{114}\:\mathrm{244}} \\ $$$${r}_{\mathrm{8}} =\frac{\mathrm{1}}{\mathrm{665}\:\mathrm{858}} \\ $$$${r}_{\mathrm{9}} =\frac{\mathrm{1}}{\mathrm{3}\:\mathrm{880}\:\mathrm{900}} \\ $$$${r}_{\mathrm{10}} =\frac{\mathrm{1}}{\mathrm{22}\:\mathrm{619}\:\mathrm{538}} \\ $$$${r}_{\mathrm{11}} =\frac{\mathrm{1}}{\mathrm{131}\:\mathrm{836}\:\mathrm{324}} \\ $$$${r}_{\mathrm{12}} =\frac{\mathrm{1}}{\mathrm{768}\:\mathrm{398}\:\mathrm{402}} \\ $$$${r}_{\mathrm{13}} =\frac{\mathrm{1}}{\mathrm{4}\:\mathrm{478}\:\mathrm{554}\:\mathrm{084}} \\ $$$${r}_{\mathrm{14}} =\frac{\mathrm{1}}{\mathrm{26}\:\mathrm{102}\:\mathrm{926}\:\mathrm{098}} \\ $$$${r}_{\mathrm{15}} =\frac{\mathrm{1}}{\mathrm{152}\:\mathrm{139}\:\mathrm{002}\:\mathrm{500}} \\ $$$${r}_{\mathrm{16}} =\frac{\mathrm{1}}{\mathrm{886}\:\mathrm{731}\:\mathrm{088}\:\mathrm{898}} \\ $$$$… \\ $$

Commented by Tawa11 last updated on 30/Dec/21

$$\mathrm{Great}\:\mathrm{sir}.\:\mathrm{Please}\:\mathrm{show}\:\mathrm{us}\:\mathrm{the}\:\mathrm{prove}\:\mathrm{sir}. \\ $$

Commented by mr W last updated on 30/Dec/21

$${it}\:{seems}\:{that}\:\frac{\mathrm{1}}{{r}_{{n}} }\:{is}\:{always}\:{an}\:{integer}. \\ $$

Commented by aleks041103 last updated on 30/Dec/21

$${I}\:{tried}\:{up}\:{to}\:{n}=\mathrm{100},\:{and}\:{indeed}\:\frac{\mathrm{1}}{{r}_{{n}} }\:{remains} \\ $$$${an}\:{integer}. \\ $$

Commented by peter frank last updated on 31/Dec/21

$$\mathrm{great}\:\mathrm{mind}\:\mathrm{think}\:\mathrm{a}\:\mathrm{like} \\ $$

Commented by mr W last updated on 01/Jan/22

$${as}\:{we}\:{can}\:{see}\:{later}, \\ $$$$\frac{\mathrm{1}}{{r}_{{n}} }=\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\mathrm{2}^{{k}} {C}_{\mathrm{2}{k}} ^{\mathrm{2}{n}} +\mathrm{1}\: \\ $$$${which}\:{is}\:{indeed}\:{always}\:{integer}. \\ $$

Answered by mr W last updated on 30/Dec/21

Commented by mr W last updated on 02/Jan/22

$${say}\:{the}\:{radius}\:{of}\:{the}\:{semicircle}\:{is}\:{R}. \\ $$$${say}\:{the}\:{biggest}\:{inscribed}\:{circle}\:{in}\:{the} \\ $$$${middle}\:{of}\:{semicircle}\:{has}\:{the}\:{radus}\:{r}_{\mathrm{0}} \\ $$$${which}\:{is}\:\frac{{R}}{\mathrm{2}}. \\ $$$${say}\:{the}\:{center}\:{of}\:{n}^{{th}} \:{inscribed}\:{circle} \\ $$$${is}\:{A}\:{and}\:{its}\:{radius}\:{is}\:{r}_{{n}} . \\ $$$${say}\:{the}\:{center}\:{of}\:\left({n}+\mathrm{1}\right)^{{th}} \:{inscribed}\: \\ $$$${circle}\:{is}\:{B}\:{and}\:{its}\:{radius}\:{is}\:{r}_{{n}+\mathrm{1}} . \\ $$$$ \\ $$$${OA}={R}−{r}_{{n}} \\ $$$${OB}={R}−{r}_{{n}+\mathrm{1}} \\ $$$${OC}=\sqrt{\left({R}−{r}_{{n}} \right)^{\mathrm{2}} −{r}_{{n}} ^{\mathrm{2}} }=\sqrt{{R}\left({R}−\mathrm{2}{r}_{{n}} \right)} \\ $$$${OD}=\sqrt{\left({R}−{r}_{{n}+\mathrm{1}} \right)^{\mathrm{2}} −{r}_{{n}+\mathrm{1}} ^{\mathrm{2}} }=\sqrt{{R}\left({R}−\mathrm{2}{r}_{{n}+\mathrm{1}} \right)} \\ $$$${AB}={r}_{{n}} +{r}_{{n}+\mathrm{1}} \\ $$$$\left({r}_{{n}} +{r}_{{n}+\mathrm{1}} \right)^{\mathrm{2}} −\left({r}_{{n}} −{r}_{{n}+\mathrm{1}} \right)^{\mathrm{2}} =\left(\sqrt{{R}\left({R}−\mathrm{2}{r}_{{n}} \right)}+\sqrt{{R}\left({R}−\mathrm{2}{r}_{{n}+\mathrm{1}} \right)}\right)^{\mathrm{2}} \\ $$$$\mathrm{2}{r}_{{n}} {r}_{{n}+\mathrm{1}} ={R}^{\mathrm{2}} −{R}\left({r}_{{n}} +{r}_{{n}+\mathrm{1}} \right)+{R}\sqrt{\left({R}−\mathrm{2}{r}_{{n}} \right)\left({R}−\mathrm{2}{r}_{{n}+\mathrm{1}} \right)} \\ $$$${let}\:\lambda_{{n}} =\frac{{r}_{{n}} }{{R}} \\ $$$$\mathrm{2}\lambda_{{n}} \lambda_{{n}+\mathrm{1}} +\lambda_{{n}} +\lambda_{{n}+\mathrm{1}} −\mathrm{1}=\sqrt{\left(\mathrm{1}−\mathrm{2}\lambda_{{n}} \right)\left(\mathrm{1}−\mathrm{2}\lambda_{{n}+\mathrm{1}} \right)} \\ $$$$\begin{array}{|c|}{\mathrm{4}\boldsymbol{\lambda}_{\boldsymbol{{n}}} ^{\mathrm{2}} \boldsymbol{\lambda}_{\boldsymbol{{n}}+\mathrm{1}} ^{\mathrm{2}} +\left(\boldsymbol{\lambda}_{\boldsymbol{{n}}} +\boldsymbol{\lambda}_{\boldsymbol{{n}}+\mathrm{1}} \right)^{\mathrm{2}} +\mathrm{4}\boldsymbol{\lambda}_{\boldsymbol{{n}}} \boldsymbol{\lambda}_{\boldsymbol{{n}}+\mathrm{1}} \left(\boldsymbol{\lambda}_{\boldsymbol{{n}}} +\boldsymbol{\lambda}_{\boldsymbol{{n}}+\mathrm{1}} −\mathrm{2}\right)=\mathrm{0}}\\\hline\end{array}\:\:…\left({I}\right) \\ $$$$\left(\mathrm{2}\lambda_{{n}} +\mathrm{1}\right)^{\mathrm{2}} \left(\frac{\lambda_{{n}+\mathrm{1}} }{\lambda_{{n}} }\right)^{\mathrm{2}} −\mathrm{2}\left(\mathrm{3}−\mathrm{2}\lambda_{{n}} \right)\left(\frac{\lambda_{{n}+\mathrm{1}} }{\lambda_{{n}} }\right)+\mathrm{1}=\mathrm{0}\: \\ $$$$\frac{\lambda_{{n}+\mathrm{1}} }{\lambda_{{n}} }=\frac{\mathrm{3}−\mathrm{2}\lambda_{{n}} −\sqrt{\left(\mathrm{3}−\mathrm{2}\lambda_{{n}} \right)^{\mathrm{2}} −\left(\mathrm{2}\lambda_{{n}} +\mathrm{1}\right)^{\mathrm{2}} }}{\left(\mathrm{2}\lambda_{{n}} +\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\frac{\lambda_{{n}+\mathrm{1}} }{\lambda_{{n}} }=\frac{\mathrm{3}−\mathrm{2}\lambda_{{n}} −\mathrm{2}\sqrt{\mathrm{2}\left(\mathrm{1}−\mathrm{2}\lambda_{{n}} \right)}}{\left(\mathrm{2}\lambda_{{n}} +\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\frac{\lambda_{{n}+\mathrm{1}} }{\lambda_{{n}} }=\frac{\mathrm{2}+\mathrm{1}−\mathrm{2}\lambda_{{n}} −\mathrm{2}\sqrt{\mathrm{2}\left(\mathrm{1}−\mathrm{2}\lambda_{{n}} \right)}}{\left(\mathrm{2}−\left(\mathrm{1}−\mathrm{2}\lambda_{{n}} \right)\right)^{\mathrm{2}} } \\ $$$$\frac{\lambda_{{n}+\mathrm{1}} }{\lambda_{{n}} }=\frac{\left(\sqrt{\mathrm{2}}−\sqrt{\mathrm{1}−\mathrm{2}\lambda_{{n}} }\right)^{\mathrm{2}} }{\left(\left(\sqrt{\mathrm{2}}\right)−\left(\sqrt{\mathrm{1}−\mathrm{2}\lambda_{{n}} }\right)^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$\frac{\lambda_{{n}+\mathrm{1}} }{\lambda_{{n}} }=\frac{\mathrm{1}}{\left(\sqrt{\mathrm{2}}+\sqrt{\mathrm{1}−\mathrm{2}\lambda_{{n}} }\right)^{\mathrm{2}} }\: \\ $$$$\frac{\mathrm{1}}{\lambda_{{n}+\mathrm{1}} }=\frac{\left(\sqrt{\mathrm{2}}+\sqrt{\mathrm{1}−\mathrm{2}\lambda_{{n}} }\right)^{\mathrm{2}} }{\lambda_{{n}} }=\frac{\mathrm{3}−\mathrm{2}\lambda_{{n}} +\mathrm{2}\sqrt{\mathrm{2}\left(\mathrm{1}−\mathrm{2}\lambda_{{n}} \right)}}{\lambda_{{n}} } \\ $$$$\Rightarrow\frac{\mathrm{1}}{\lambda_{{n}+\mathrm{1}} }=\frac{\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}\left(\mathrm{1}−\mathrm{2}\lambda_{{n}} \right)}}{\lambda_{{n}} }−\mathrm{2}\:\:\:…\left({i}\right) \\ $$$$ \\ $$$${we}\:{can}\:{transform}\:{eqn}.\:\left({I}\right)\:{also}\:{into} \\ $$$$\left(\mathrm{2}\lambda_{{n}+\mathrm{1}} +\mathrm{1}\right)^{\mathrm{2}} \left(\frac{\lambda_{{n}} }{\lambda_{{n}+\mathrm{1}} }\right)^{\mathrm{2}} −\mathrm{2}\left(\mathrm{3}−\mathrm{2}\lambda_{{n}+\mathrm{1}} \right)\left(\frac{\lambda_{{n}} }{\lambda_{{n}+\mathrm{1}} }\right)+\mathrm{1}=\mathrm{0} \\ $$$$\frac{\lambda_{{n}} }{\lambda_{{n}+\mathrm{1}} }=\frac{\mathrm{3}−\mathrm{2}\lambda_{{n}+\mathrm{1}} +\sqrt{\left(\mathrm{3}−\mathrm{2}\lambda_{{n}+\mathrm{1}} \right)^{\mathrm{2}} −\left(\mathrm{2}\lambda_{{n}+\mathrm{1}} +\mathrm{1}\right)^{\mathrm{2}} }}{\left(\mathrm{2}\lambda_{{n}+\mathrm{1}} +\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${similarly}\:{to}\:{above}, \\ $$$$\frac{\lambda_{{n}} }{\lambda_{{n}+\mathrm{1}} }=\frac{\mathrm{1}}{\left(\sqrt{\mathrm{2}}−\sqrt{\mathrm{1}−\mathrm{2}\lambda_{{n}+\mathrm{1}} }\right)^{\mathrm{2}} } \\ $$$$\frac{\mathrm{1}}{\lambda_{{n}} }=\frac{\left(\sqrt{\mathrm{2}}−\sqrt{\mathrm{1}−\mathrm{2}\lambda_{{n}+\mathrm{1}} }\right)^{\mathrm{2}} }{\lambda_{{n}+\mathrm{1}} }=\frac{\mathrm{3}−\mathrm{2}\lambda_{{n}+\mathrm{1}} −\mathrm{2}\sqrt{\mathrm{2}\left(\mathrm{1}−\mathrm{2}\lambda_{{n}+\mathrm{1}} \right)}}{\lambda_{{n}+\mathrm{1}} } \\ $$$$\frac{\mathrm{1}}{\lambda_{{n}} }=\frac{\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}\left(\mathrm{1}−\mathrm{2}\lambda_{{n}+\mathrm{1}} \right)}}{\lambda_{{n}+\mathrm{1}} }−\mathrm{2} \\ $$$${or} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\lambda_{{n}−\mathrm{1}} }=\frac{\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}\left(\mathrm{1}−\mathrm{2}\lambda_{{n}} \right)}}{\lambda_{{n}} }−\mathrm{2}\:\:\:…\left({ii}\right) \\ $$$$ \\ $$$$\left({i}\right)+\left({ii}\right): \\ $$$$\frac{\mathrm{1}}{\lambda_{{n}+\mathrm{1}} }+\frac{\mathrm{1}}{\lambda_{{n}−\mathrm{1}} }=\frac{\mathrm{6}}{\lambda_{{n}} }−\mathrm{4} \\ $$$$\begin{array}{|c|}{\frac{\mathrm{1}}{\lambda_{{n}+\mathrm{1}} }−\frac{\mathrm{6}}{\lambda_{{n}} }+\frac{\mathrm{1}}{\lambda_{{n}−\mathrm{1}} }+\mathrm{4}=\mathrm{0}}\\\hline\end{array} \\ $$$${let}\:\frac{\mathrm{1}}{\lambda_{{n}} }=\xi_{{n}} +{c} \\ $$$$\left(\xi_{{n}+\mathrm{1}} +{c}\right)−\mathrm{6}\left(\xi_{{n}} +{c}\right)+\left(\xi_{{n}−\mathrm{1}} +{c}\right)+\mathrm{4}=\mathrm{0} \\ $$$$\xi_{{n}+\mathrm{1}} −\mathrm{6}\xi_{{n}} +\xi_{{n}−\mathrm{1}} +\mathrm{4}−\mathrm{4}{c}=\mathrm{0} \\ $$$${set}\:\mathrm{4}−\mathrm{4}{c}=\mathrm{0},\:{i}.{e}.\:{c}=\mathrm{1} \\ $$$$\Rightarrow\xi_{{n}+\mathrm{1}} −\mathrm{6}\xi_{{n}} +\xi_{{n}−\mathrm{1}} =\mathrm{0} \\ $$$${x}^{\mathrm{2}} −\mathrm{6}{x}+\mathrm{1}=\mathrm{0}\:\:\left({characteristic}\:{eqn}.\right) \\ $$$$\Rightarrow{x}=\mathrm{3}\pm\mathrm{2}\sqrt{\mathrm{2}}=\left(\sqrt{\mathrm{2}}\pm\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\xi_{{n}} ={A}\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)^{\mathrm{2}{n}} +{B}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)^{\mathrm{2}{n}} \\ $$$$\frac{\mathrm{1}}{\lambda_{{n}} }={A}\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)^{\mathrm{2}{n}} +{B}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)^{\mathrm{2}{n}} +\mathrm{1} \\ $$$$\lambda_{\mathrm{0}} =\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{2}={A}+{B}+\mathrm{1}\:\Rightarrow{A}+{B}=\mathrm{1} \\ $$$$\lambda_{\mathrm{1}} =\lambda_{−\mathrm{1}} \:{due}\:{to}\:{symmetry} \\ $$$${A}\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)^{\mathrm{2}} +{B}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}={A}\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)^{−\mathrm{2}} +{B}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)^{−\mathrm{2}} +\mathrm{1} \\ $$$${A}\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)^{\mathrm{2}} +{B}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)^{\mathrm{2}} ={A}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)^{\mathrm{2}} +{B}\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\left({A}−{B}\right)\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)^{\mathrm{2}} =\left({A}−{B}\right)\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\Rightarrow{A}={B}\:\Rightarrow{A}={B}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\begin{array}{|c|}{\frac{\mathrm{1}}{\lambda_{{n}} }=\frac{\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)^{\mathrm{2}{n}} +\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)^{\mathrm{2}{n}} }{\mathrm{2}}+\mathrm{1}}\\\hline\end{array} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\lambda_{{n}} }=\frac{\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)^{\mathrm{2}{n}} +\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)^{−\mathrm{2}{n}} +\mathrm{2}}{\mathrm{2}} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\lambda_{{n}} }=\mathrm{2}×\left[\frac{\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)^{{n}} +\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)^{−{n}} }{\mathrm{2}}\right]^{\mathrm{2}} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\lambda_{{n}} }=\mathrm{2}×\left[\frac{{e}^{{n}\mathrm{ln}\:\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)} +{e}^{−{n}\mathrm{ln}\:\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)} }{\mathrm{2}}\right]^{\mathrm{2}} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\lambda_{{n}} }=\mathrm{2}\:\mathrm{cosh}^{\mathrm{2}} \:\left[{n}\mathrm{ln}\:\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)\right] \\ $$$$\begin{array}{|c|}{{r}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}\:\mathrm{cosh}^{\mathrm{2}} \:\left[{n}\mathrm{ln}\:\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)\right]}}\\\hline\end{array} \\ $$$$ \\ $$$${total}\:{area}\:{of}\:{all}\:{red}\:{circles}: \\ $$$${A}=\pi{r}_{\mathrm{0}} ^{\mathrm{2}} +\mathrm{2}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\pi{r}_{{n}} ^{\mathrm{2}} \\ $$$${A}=\frac{\pi}{\mathrm{4}}+\frac{\pi}{\mathrm{2}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{cosh}^{\mathrm{4}} \:\left[{n}\mathrm{ln}\:\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)\right]} \\ $$$$\:\:\:\:\approx\mathrm{1}.\mathrm{198}\:\mathrm{137}\:\mathrm{490}\:\left(\mathrm{76\%}\:{of}\:{semicircle}\right) \\ $$$$ \\ $$$$\underline{\boldsymbol{{additional}}\:\boldsymbol{{note}}:} \\ $$$${we}\:{can}\:{also}\:{proceed}\:{as}\:{following}: \\ $$$$\frac{\mathrm{1}}{{r}_{{n}} }=\frac{\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)^{\mathrm{2}{n}} +\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)^{\mathrm{2}{n}} }{\mathrm{2}}+\mathrm{1} \\ $$$$\frac{\mathrm{1}}{{r}_{{n}} }=\frac{\underset{{k}=\mathrm{0}} {\overset{\mathrm{2}{n}} {\sum}}{C}_{{k}} ^{\mathrm{2}{n}} \left(\sqrt{\mathrm{2}}\right)^{{k}} +\underset{{k}=\mathrm{0}} {\overset{\mathrm{2}{n}} {\sum}}{C}_{{k}} ^{\mathrm{2}{n}} \left(\sqrt{\mathrm{2}}\right)^{{k}} \left(−\mathrm{1}\right)^{\mathrm{2}{n}−{k}} }{\mathrm{2}}+\mathrm{1} \\ $$$$\frac{\mathrm{1}}{{r}_{{n}} }=\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\mathrm{2}^{{k}} {C}_{\mathrm{2}{k}} ^{\mathrm{2}{n}} +\mathrm{1} \\ $$$${this}\:{is}\:{clearly}\:{always}\:{an}\:{even}\:{integer}. \\ $$$$ \\ $$$$\left[{completed}\:{on}\:\mathrm{01}/\mathrm{01}/\mathrm{2022},\:\mathrm{2}:\mathrm{00}{h}\right] \\ $$

Commented by Tawa11 last updated on 30/Dec/21

$$\mathrm{Wow},\:\mathrm{thanks}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{more}. \\ $$

Commented by Tawa11 last updated on 30/Dec/21

$$\mathrm{Thanks}\:\mathrm{for}\:\mathrm{your}\:\mathrm{time}\:\mathrm{sir} \\ $$

Commented by ajfour last updated on 22/Jan/22

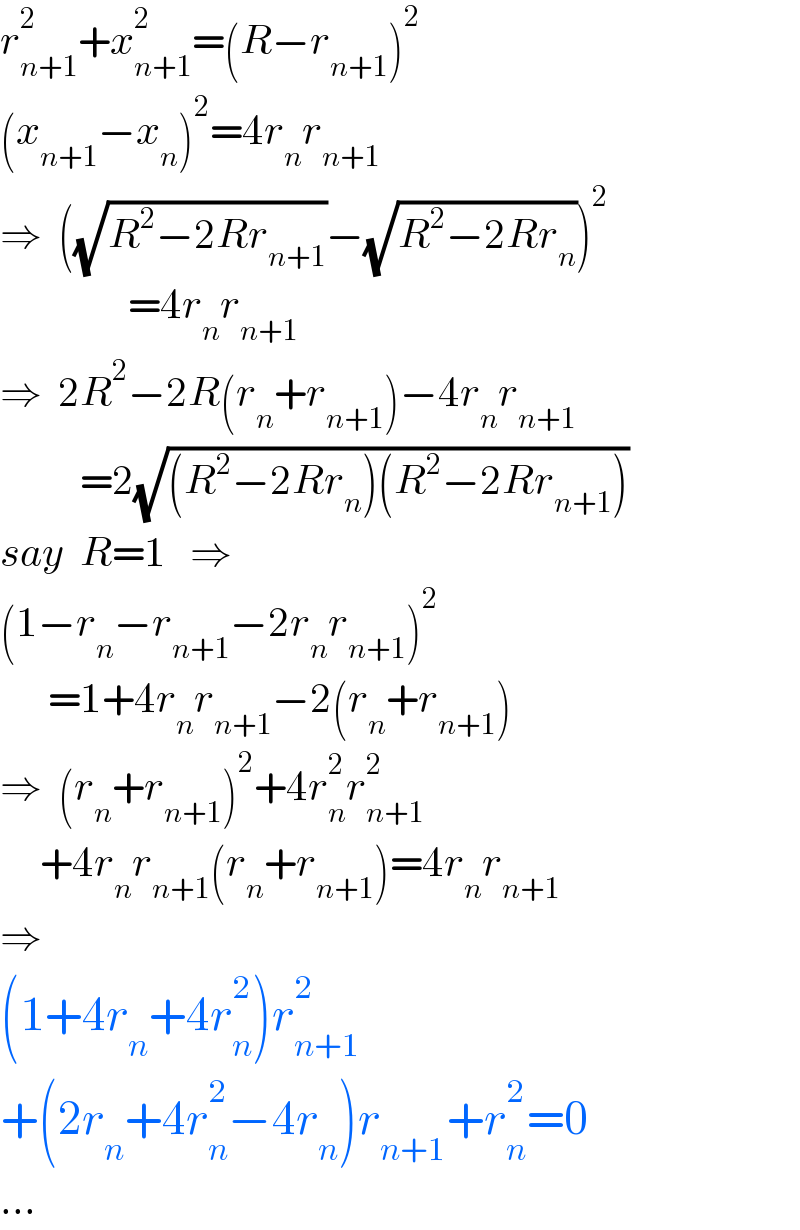
$${r}_{{n}+\mathrm{1}} ^{\mathrm{2}} +{x}_{{n}+\mathrm{1}} ^{\mathrm{2}} =\left({R}−{r}_{{n}+\mathrm{1}} \right)^{\mathrm{2}} \\ $$$$\left({x}_{{n}+\mathrm{1}} −{x}_{{n}} \right)^{\mathrm{2}} =\mathrm{4}{r}_{{n}} {r}_{{n}+\mathrm{1}} \\ $$$$\Rightarrow\:\:\left(\sqrt{{R}^{\mathrm{2}} −\mathrm{2}{Rr}_{{n}+\mathrm{1}} }−\sqrt{{R}^{\mathrm{2}} −\mathrm{2}{Rr}_{{n}} }\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{4}{r}_{{n}} {r}_{{n}+\mathrm{1}} \\ $$$$\Rightarrow\:\:\mathrm{2}{R}^{\mathrm{2}} −\mathrm{2}{R}\left({r}_{{n}} +{r}_{{n}+\mathrm{1}} \right)−\mathrm{4}{r}_{{n}} {r}_{{n}+\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\mathrm{2}\sqrt{\left({R}^{\mathrm{2}} −\mathrm{2}{Rr}_{{n}} \right)\left({R}^{\mathrm{2}} −\mathrm{2}{Rr}_{{n}+\mathrm{1}} \right)} \\ $$$${say}\:\:{R}=\mathrm{1}\:\:\:\Rightarrow \\ $$$$\left(\mathrm{1}−{r}_{{n}} −{r}_{{n}+\mathrm{1}} −\mathrm{2}{r}_{{n}} {r}_{{n}+\mathrm{1}} \right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:=\mathrm{1}+\mathrm{4}{r}_{{n}} {r}_{{n}+\mathrm{1}} −\mathrm{2}\left({r}_{{n}} +{r}_{{n}+\mathrm{1}} \right) \\ $$$$\Rightarrow\:\:\left({r}_{{n}} +{r}_{{n}+\mathrm{1}} \right)^{\mathrm{2}} +\mathrm{4}{r}_{{n}} ^{\mathrm{2}} {r}_{{n}+\mathrm{1}} ^{\mathrm{2}} \\ $$$$\:\:\:\:\:+\mathrm{4}{r}_{{n}} {r}_{{n}+\mathrm{1}} \left({r}_{{n}} +{r}_{{n}+\mathrm{1}} \right)=\mathrm{4}{r}_{{n}} {r}_{{n}+\mathrm{1}} \\ $$$$\Rightarrow \\ $$$$\left(\mathrm{1}+\mathrm{4}{r}_{{n}} +\mathrm{4}{r}_{{n}} ^{\mathrm{2}} \right){r}_{{n}+\mathrm{1}} ^{\mathrm{2}} \\ $$$$+\left(\mathrm{2}{r}_{{n}} +\mathrm{4}{r}_{{n}} ^{\mathrm{2}} −\mathrm{4}{r}_{{n}} \right){r}_{{n}+\mathrm{1}} +{r}_{{n}} ^{\mathrm{2}} =\mathrm{0} \\ $$$$… \\ $$

Answered by aleks041103 last updated on 30/Dec/21

Commented by aleks041103 last updated on 30/Dec/21

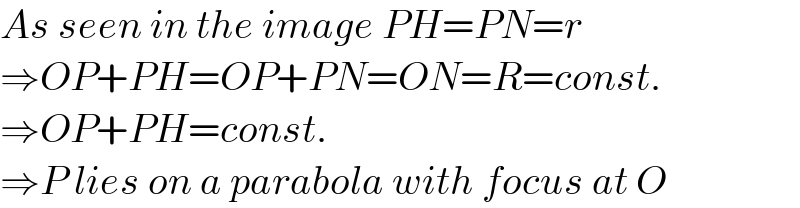
$${As}\:{seen}\:{in}\:{the}\:{image}\:{PH}={PN}={r} \\ $$$$\Rightarrow{OP}+{PH}={OP}+{PN}={ON}={R}={const}. \\ $$$$\Rightarrow{OP}+{PH}={const}. \\ $$$$\Rightarrow{P}\:{lies}\:{on}\:{a}\:{parabola}\:{with}\:{focus}\:{at}\:{O} \\ $$

Commented by aleks041103 last updated on 30/Dec/21

$${that}'{s}\:{just}\:{interesting}\:{to}\:{note}. \\ $$

Commented by aleks041103 last updated on 31/Dec/21

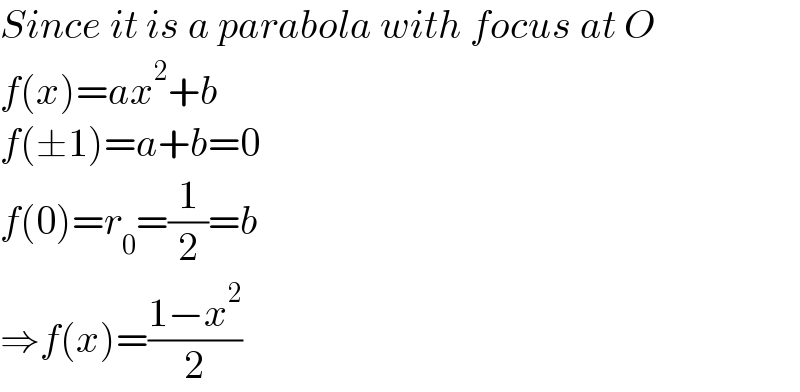
$${Since}\:{it}\:{is}\:{a}\:{parabola}\:{with}\:{focus}\:{at}\:{O} \\ $$$${f}\left({x}\right)={ax}^{\mathrm{2}} +{b} \\ $$$${f}\left(\pm\mathrm{1}\right)={a}+{b}=\mathrm{0} \\ $$$${f}\left(\mathrm{0}\right)={r}_{\mathrm{0}} =\frac{\mathrm{1}}{\mathrm{2}}={b} \\ $$$$\Rightarrow{f}\left({x}\right)=\frac{\mathrm{1}−{x}^{\mathrm{2}} }{\mathrm{2}} \\ $$

Commented by mr W last updated on 31/Dec/21

$${alex}\:{sir}: \\ $$$${yes},\:{the}\:{locus}\:{of}\:{the}\:{center}\:{of}\:{a}\:{circle} \\ $$$${inscribed}\:{in}\:{a}\:{circular}\:{segment}\:{is} \\ $$$${a}\:{parabola}. \\ $$

Commented by mr W last updated on 31/Dec/21

Commented by aleks041103 last updated on 31/Dec/21

$${mr}\:{W},\:{how}\:{are}\:{you}\:{making}\:{those}\:{drawings}? \\ $$

Commented by mr W last updated on 22/Jan/22

$${the}\:{diagram}\:{is}\:{made}\:{with} \\ $$$${the}\:{App}\:{LEHK}\:{DIAGRAM} \\ $$$$\left({recommended}\:{by}\:{Ajfour}\:{sir}\right) \\ $$

Answered by aleks041103 last updated on 31/Dec/21

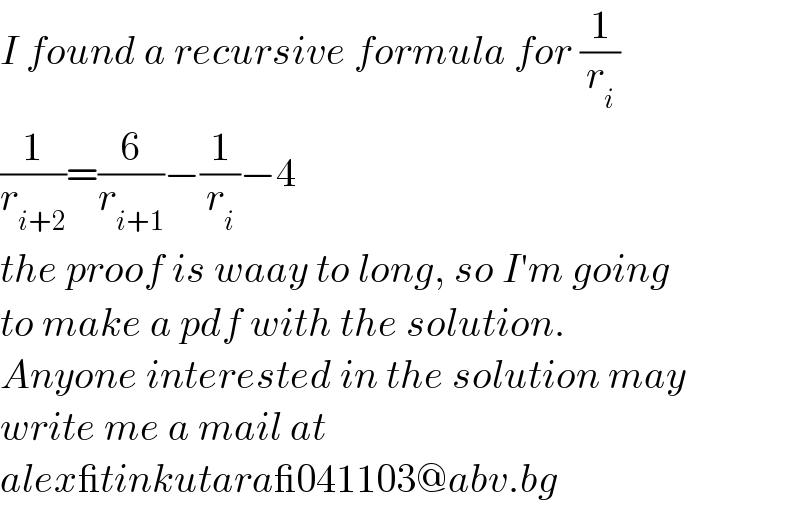
$${I}\:{found}\:{a}\:{recursive}\:{formula}\:{for}\:\frac{\mathrm{1}}{{r}_{{i}} } \\ $$$$\frac{\mathrm{1}}{{r}_{{i}+\mathrm{2}} }=\frac{\mathrm{6}}{{r}_{{i}+\mathrm{1}} }−\frac{\mathrm{1}}{{r}_{{i}} }−\mathrm{4} \\ $$$${the}\:{proof}\:{is}\:{waay}\:{to}\:{long},\:{so}\:{I}'{m}\:{going} \\ $$$${to}\:{make}\:{a}\:{pdf}\:{with}\:{the}\:{solution}. \\ $$$${Anyone}\:{interested}\:{in}\:{the}\:{solution}\:{may} \\ $$$${write}\:{me}\:{a}\:{mail}\:{at}\: \\ $$$${alex\_tinkutara\_}\mathrm{041103}@{abv}.{bg} \\ $$

Commented by aleks041103 last updated on 31/Dec/21

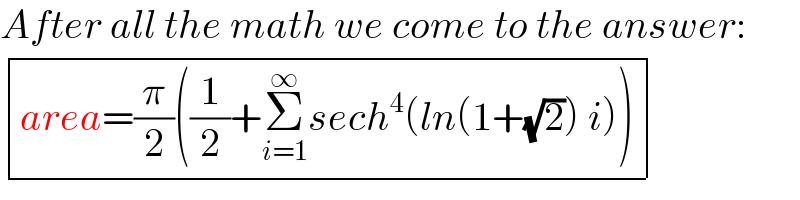
$${After}\:{all}\:{the}\:{math}\:{we}\:{come}\:{to}\:{the}\:{answer}: \\ $$$$\begin{array}{|c|}{{area}=\frac{\pi}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{2}}+\underset{{i}=\mathrm{1}} {\overset{\infty} {\sum}}{sech}^{\mathrm{4}} \left({ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)\:{i}\right)\right)}\\\hline\end{array} \\ $$

Commented by aleks041103 last updated on 31/Dec/21

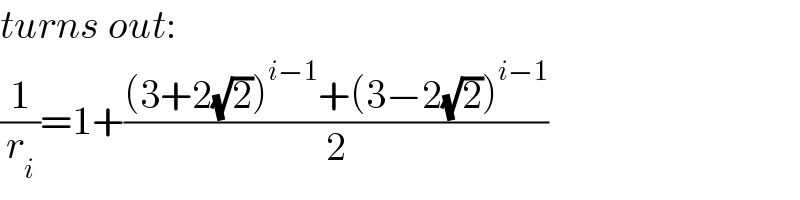
$${turns}\:{out}: \\ $$$$\frac{\mathrm{1}}{{r}_{{i}} }=\mathrm{1}+\frac{\left(\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}\right)^{{i}−\mathrm{1}} +\left(\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}}\right)^{{i}−\mathrm{1}} }{\mathrm{2}} \\ $$

Commented by mr W last updated on 31/Dec/21

$${i}\:{knew}\:{you}\:{will}\:{arrive}\:{at}\:{the}\:{final} \\ $$$${solution}.\:{it}'{s}\:{perfect}\:{again}\:{sir}.\:{you} \\ $$$${have}\:{solved}\:{a}\:{problem}\:{which}\:{seemed} \\ $$$${unsolvable}.\:{really}\:{great}\:{job}! \\ $$

Commented by aleks041103 last updated on 31/Dec/21

$${mr}\:{W},\:{I}\:{really}\:{want}\:{to}\:{share}\:{my}\:{solution} \\ $$$${with}\:{you}.\:{If}\:{you}\:{want}\:{you}\:{can}\:{type}\:{your}\:{email}\: \\ $$$${address}\:{here},\:{or}\:{just}\:{write}\:{me}\:{an}\:{email} \\ $$$${at}\:{alex\_tinkutara\_}\mathrm{041103}@{abv}.{bg} \\ $$

Commented by mr W last updated on 31/Dec/21

$${thanks}\:{alot}\:{sir}!\:{i}'{m}\:{very}\:{interested}. \\ $$$${i}'{ll}\:{also}\:{try}\:{if}\:{i}\:{could}\:{come}\:{to}\:{the} \\ $$$${same}\:{result}.\:{maybe}\:{you}\:{can}\:{publish} \\ $$$${your}\:{solution}\:{here}\:{so}\:{that}\:{more} \\ $$$${people}\:{can}\:{benifit}\:{from}\:{it}.\:{you}\:{don}'{t} \\ $$$${need}\:{to}\:{typewrite}\:{it},\:{you}\:{can}\:{also} \\ $$$${make}\:{a}\:{photo}\:{from}\:{your}\:{handwriting} \\ $$$${or}\:{from}\:{your}\:{pdf},\:{and}\:{then}\:{post}\:{the} \\ $$$${image}\:{here}. \\ $$

Commented by mr W last updated on 01/Jan/22

$${alex}\:{sir}: \\ $$$${i}\:{could}\:{come}\:{to}\:{the}\:{same}\:{result}.\:{please} \\ $$$${review}\:{my}\:{completed}\:{working}\:{above}. \\ $$$${thanks}\:{for}\:{your}\:{support}! \\ $$

Answered by aleks041103 last updated on 01/Jan/22

Commented by aleks041103 last updated on 01/Jan/22

Commented by aleks041103 last updated on 01/Jan/22

Commented by aleks041103 last updated on 01/Jan/22

Commented by aleks041103 last updated on 01/Jan/22

Commented by aleks041103 last updated on 01/Jan/22

Commented by aleks041103 last updated on 01/Jan/22

Commented by aleks041103 last updated on 01/Jan/22

Commented by aleks041103 last updated on 01/Jan/22

Commented by aleks041103 last updated on 01/Jan/22

Commented by aleks041103 last updated on 01/Jan/22

Commented by aleks041103 last updated on 01/Jan/22

Commented by aleks041103 last updated on 01/Jan/22

Commented by aleks041103 last updated on 01/Jan/22

Commented by mr W last updated on 01/Jan/22

$${i}\:{have}\:{followed}\:{your}\:{working}.\:{it}'{s}\: \\ $$$${amazing}\:{how}\:{you}\:{analysed}\:{the}\:{thing} \\ $$$${and}\:{got}\:{the}\:{recursive}\:{relation}.\: \\ $$$${i}\:{used}\:{a}\:{different}\:{way}\:{for}\:{my}\:{solution}, \\ $$$${which}\:{even}\:{looks}\:{a}\:{little}\:{bit}\:{easier}\: \\ $$$${than}\:{yours}.\:{but}\:{to}\:{be}\:{honest},\:{without}\: \\ $$$${your}\:{result},\:{i}\:{even}\:{have}\:{stoped}\:{to}\:{go}\: \\ $$$${further}\:{and}\:{have}\:{accepted}\:{that}\:{it}'{s}\: \\ $$$${impossible}\:{to}\:{solve}\:{for}\:{r}_{{n}} \:{in}\:{terms}\: \\ $$$${of}\:{n}. \\ $$

Commented by mr W last updated on 01/Jan/22

$${wow}!\:{what}\:{an}\:{effort}\:{you}\:{made}! \\ $$$${you}\:{have}\:{really}\:{done}\:{a}\:{great}\:{job}! \\ $$$${it}\:{looks}\:{like}\:{a}\:{scientific}\:{paper}\:{which} \\ $$$${you}\:{can}\:{publish}\:{in}\:{magazines}. \\ $$

Terms of Service
Privacy Policy
Contact: info@tinkutara.com