Question-162561

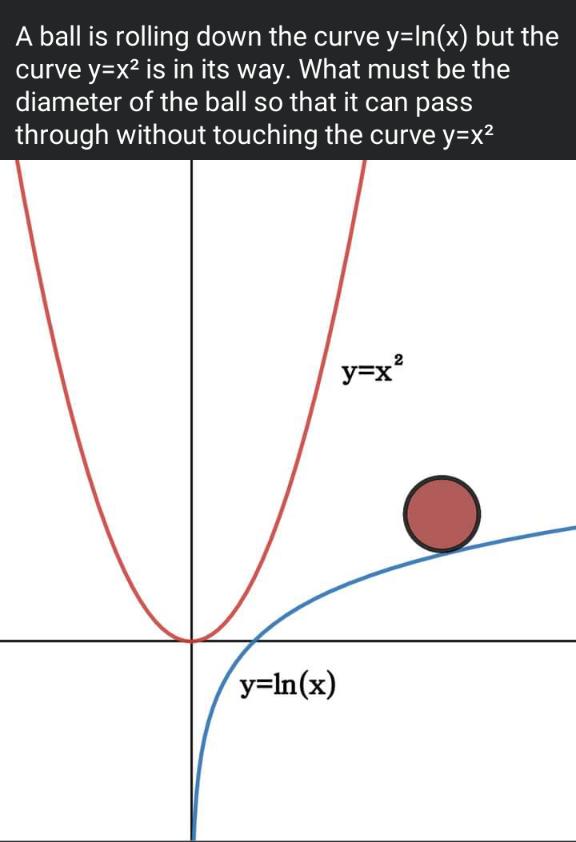
Question Number 162561 by Mathematification last updated on 30/Dec/21

Answered by MJS_new last updated on 30/Dec/21

we have to find the minimum value of ∣AB∣ with A= ((p),(p^2 ) ) and B= ((q),((ln q)) ) . this can only be approximated. I get p≈.538167 q≈.929078 ∣AB∣=d≈.533588 from the parallel tangents we get q=(1/(2p)) ⇒ now it′s easier to approximate p≈.538167720574 q≈.929078391150 d≈.533587574933

$$\mathrm{we}\:\mathrm{have}\:\mathrm{to}\:\mathrm{find}\:\mathrm{the}\:\mathrm{minimum}\:\mathrm{value}\:\mathrm{of}\:\mid{AB}\mid \\ $$$$\mathrm{with}\:{A}=\begin{pmatrix}{{p}}\\{{p}^{\mathrm{2}} }\end{pmatrix}\:\mathrm{and}\:{B}=\begin{pmatrix}{{q}}\\{\mathrm{ln}\:{q}}\end{pmatrix}\:.\:\mathrm{this}\:\mathrm{can}\:\mathrm{only} \\ $$$$\mathrm{be}\:\mathrm{approximated}.\:\mathrm{I}\:\mathrm{get} \\ $$$${p}\approx.\mathrm{538167} \\ $$$${q}\approx.\mathrm{929078} \\ $$$$\mid{AB}\mid={d}\approx.\mathrm{533588} \\ $$$$\mathrm{from}\:\mathrm{the}\:\mathrm{parallel}\:\mathrm{tangents}\:\mathrm{we}\:\mathrm{get}\:{q}=\frac{\mathrm{1}}{\mathrm{2}{p}}\:\Rightarrow \\ $$$$\mathrm{now}\:\mathrm{it}'\mathrm{s}\:\mathrm{easier}\:\mathrm{to}\:\mathrm{approximate} \\ $$$${p}\approx.\mathrm{538167720574} \\ $$$${q}\approx.\mathrm{929078391150} \\ $$$${d}\approx.\mathrm{533587574933} \\ $$

Answered by mr W last updated on 30/Dec/21

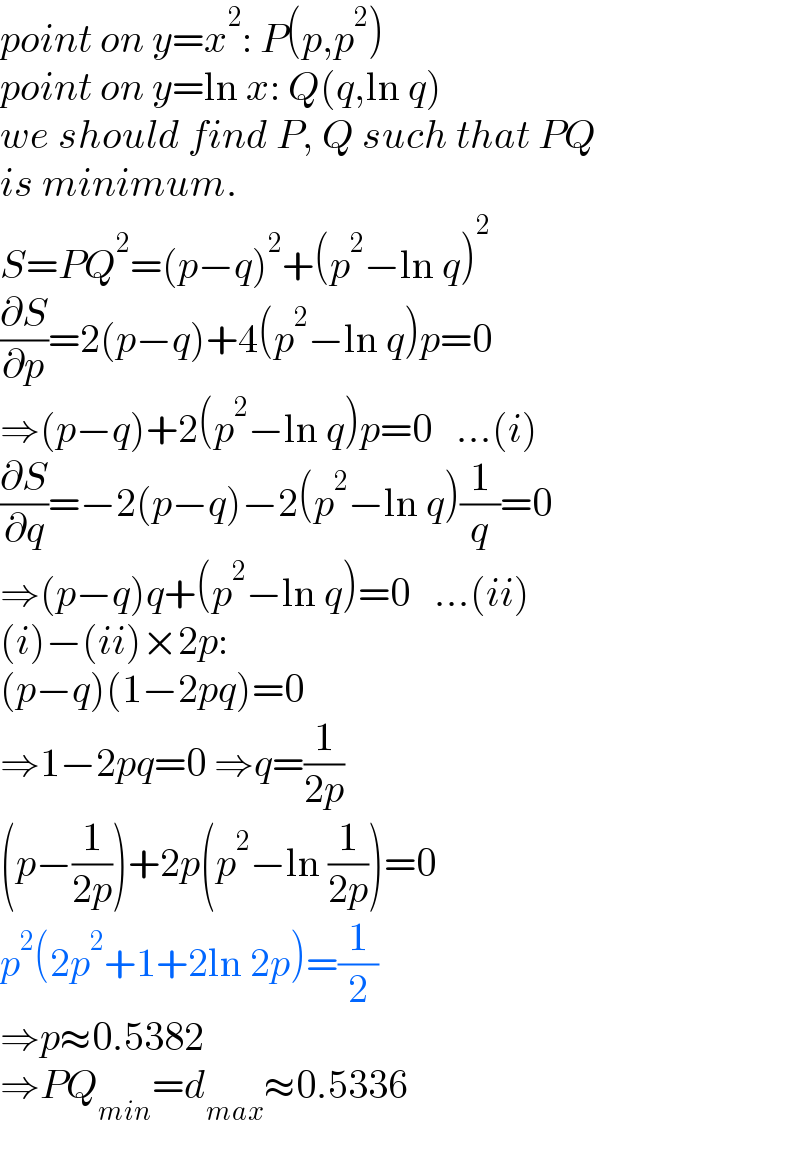
point on y=x^2 : P(p,p^2 ) point on y=ln x: Q(q,ln q) we should find P, Q such that PQ is minimum. S=PQ^2 =(p−q)^2 +(p^2 −ln q)^2 (∂S/∂p)=2(p−q)+4(p^2 −ln q)p=0 ⇒(p−q)+2(p^2 −ln q)p=0 ...(i) (∂S/∂q)=−2(p−q)−2(p^2 −ln q)(1/q)=0 ⇒(p−q)q+(p^2 −ln q)=0 ...(ii) (i)−(ii)×2p: (p−q)(1−2pq)=0 ⇒1−2pq=0 ⇒q=(1/(2p)) (p−(1/(2p)))+2p(p^2 −ln (1/(2p)))=0 p^2 (2p^2 +1+2ln 2p)=(1/2) ⇒p≈0.5382 ⇒PQ_(min) =d_(max) ≈0.5336

$${point}\:{on}\:{y}={x}^{\mathrm{2}} :\:{P}\left({p},{p}^{\mathrm{2}} \right) \\ $$$${point}\:{on}\:{y}=\mathrm{ln}\:{x}:\:{Q}\left({q},\mathrm{ln}\:{q}\right) \\ $$$${we}\:{should}\:{find}\:{P},\:{Q}\:{such}\:{that}\:{PQ} \\ $$$${is}\:{minimum}. \\ $$$${S}={PQ}^{\mathrm{2}} =\left({p}−{q}\right)^{\mathrm{2}} +\left({p}^{\mathrm{2}} −\mathrm{ln}\:{q}\right)^{\mathrm{2}} \\ $$$$\frac{\partial{S}}{\partial{p}}=\mathrm{2}\left({p}−{q}\right)+\mathrm{4}\left({p}^{\mathrm{2}} −\mathrm{ln}\:{q}\right){p}=\mathrm{0} \\ $$$$\Rightarrow\left({p}−{q}\right)+\mathrm{2}\left({p}^{\mathrm{2}} −\mathrm{ln}\:{q}\right){p}=\mathrm{0}\:\:\:…\left({i}\right) \\ $$$$\frac{\partial{S}}{\partial{q}}=−\mathrm{2}\left({p}−{q}\right)−\mathrm{2}\left({p}^{\mathrm{2}} −\mathrm{ln}\:{q}\right)\frac{\mathrm{1}}{{q}}=\mathrm{0} \\ $$$$\Rightarrow\left({p}−{q}\right){q}+\left({p}^{\mathrm{2}} −\mathrm{ln}\:{q}\right)=\mathrm{0}\:\:\:…\left({ii}\right) \\ $$$$\left({i}\right)−\left({ii}\right)×\mathrm{2}{p}: \\ $$$$\left({p}−{q}\right)\left(\mathrm{1}−\mathrm{2}{pq}\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{1}−\mathrm{2}{pq}=\mathrm{0}\:\Rightarrow{q}=\frac{\mathrm{1}}{\mathrm{2}{p}} \\ $$$$\left({p}−\frac{\mathrm{1}}{\mathrm{2}{p}}\right)+\mathrm{2}{p}\left({p}^{\mathrm{2}} −\mathrm{ln}\:\frac{\mathrm{1}}{\mathrm{2}{p}}\right)=\mathrm{0} \\ $$$${p}^{\mathrm{2}} \left(\mathrm{2}{p}^{\mathrm{2}} +\mathrm{1}+\mathrm{2ln}\:\mathrm{2}{p}\right)=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow{p}\approx\mathrm{0}.\mathrm{5382} \\ $$$$\Rightarrow{PQ}_{{min}} ={d}_{{max}} \approx\mathrm{0}.\mathrm{5336} \\ $$

Commented by mr W last updated on 30/Dec/21